Постановка задачи Коши

Тема 6. Численное решение дифференциальных уравнений

Известно, что обыкновенное дифференциальное уравнение первого порядка имеет вид:

y' (t) = f (t, y (t)). (6.1)

Решением уравнения (6.1) является дифференцируемая функция y (t), которая при подстановке в уравнение (6.1) обращает его в тождество. На рис. 6.1 приведен график решения дифференциального уравнения (6.1). График решения дифференциального уравнения называется интегральной кривой.

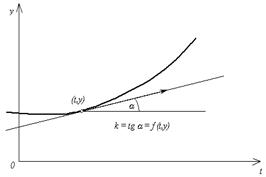
Рис. 6.1

Производную y' (t) в каждой точке (t, y) можно геометрически интерпретировать как тангенс угла a наклона касательной к графику решения, проходящего через эту точку, т е.: k = tga = f (t, y).

Уравнение (6.1) определяет целое семейство решений. Чтобы выделить одно решение, задают начальное условие:

y (t ₀ ) = y ₀, (6.2)

где t ₀ – некоторое заданное значение аргумента t, а y ₀ – начальное значение функции.

Задача Коши заключается в отыскании функции y = y (t), удовлетворяющей уравнению (6.1) и начальному условию (6.2). Обычно определяют решение задачи Коши на отрезке, расположенном справа от начального значения t ₀, т. е. для t Î [ t ₀, T ].

Разрешимость задачи Коши определяет следующая теорема.

Теорема 6.1. Пусть функция f (t, y) определена и непрерывна при t ₀ £ t £ T, -¥ < y < ¥ и удовлетворяет условию Липшица:

| f (t, y ₁) – f (t, y ₂)| £ L | y ₁ – y ₂|,

где L некоторая постоянная, а y ₁, y ₂ – произвольные значения.

Тогда для каждого начального значения y ₀ существует единственное решение y (t) задачи Коши для t Î [ t ₀, T ].

Даже для простых дифференциальных уравнений первого порядка не всегда удается получить аналитическое решение. Поэтому большое значение имеют численные методы решения. Численные методы позволяют определить приближенные значения искомого решения y (t) на некоторой выбранной сетке значений аргумента t_i, (i = 0, 1, …). Точки t_i называются узлами сетки, а величина h_i = t_{i +1} – t_i – шагом сетки. Часто рассматривают равномерные сетки, для которых шаг h_i постоянен, h_i = h = . При этом решение получается в виде таблицы, в которой каждому узлу сетки t_i соответствуют приближенные значения функции y (t) в узлах сетки y_i» y (t_i).

Численные методы не позволяют найти решение в общем виде, зато они применимы к широкому классу дифференциальных уравнений.

Сходимость численных методов решения задачи Коши. Пусть y (t) – решение задачи Коши. Назовем глобальной погрешностью (или просто погрешностью) численного метода функцию e_i = y (t_i) – y_i, заданную в узлах сетки t_i. В качестве абсолютной погрешности примем величину R = 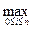| y (t_i) – y_i |

Численный метод решения задачи Коши называется сходящимся, если для него R ® 0 при h ® 0. Говорят, что метод имеет p -ый порядок точности, если для погрешности справедлива оценка R £ Ch^p, p > 0, C – константа, C ¹ 0.

Дата добавления: 2014-01-05