Міри близькості на ранжуваннях

Способи отримання мір близькості

Міри близькості на бінарних відношеннях

У задачах прийняття рішень із використанням бінарних відношень постійно виникають проблеми порівняння бінарних відношень, визначення ступеня близькості, пошуку в певному розумінні середніх відношень або апроксимації емпіричних відношень тими, що мають задані властивості. Розв’язуючи ці проблеми, всюди використовують поняття «віддалі» між відношеннями. Тому для вимірювання віддалей потрібно запровадити певну метрику, міру близькості. Загальновизнаний метод одержання формул або алгоритмів обчислення віддалей між відношеннями – це аксіоматичний.

У цьому випадку слід виконати таку послідовність кроків.

1. Формулювання системи аксіом, що задовольняють певні вимоги та припущення.

2. Доведення теореми існування однієї й лише однієї міри близькості на відношеннях, що ґрунтуються на побудованій системі аксіом.

3. Отримання формули (чи алгоритму) для визначення міри близькості.

У реальних умовах вибір і обґрунтування можливостей використання тієї чи іншої міри близькості покладають на аналітичну групу, яка бере до уваги первинні вимоги. Уперше аксіоматичну міру близькості побудував Дж.Кемені для відношень лінійного порядку. Пізніше було одержано міри близькості на відношеннях еквівалентності, порядку, толерантності, метризованих відношеннях і відношеннях загального вигляду. Окрім того, значення деяких мір близькості обчислюють за допомогою розв’язання оптимізаційних задач (про найкоротший шлях, наплічник і т. ін.).

Наявність мір близькості дає змогу ставити й розв’язувати такі практично важливі задачі:

v будувати остаточні відношення за тими, які отримано від експертів;

v шукати найближче до експертного відношення з певними властивостями;

v класифікувати експертів за результатами побудованих ними бінарних відношень;

v формулювати узагальнені критерії та перевіряти рівень суперечливості експертів.

Розглянемо послідовність побудови міри близькості на відношеннях лінійного порядку (ранжуваннях) із використанням результатів Дж.Кемені. Сформулюємо систему аксіом, які мають виконуватись у разі використання метрики. По–перше, для довільної міри близькості мають бути виконані три основні аксіоми метрики: невід’ємності, симетричності віддалі та трикутника.

АКСІОМА 1. (невід’ємності відстані). Віддаль d між двома довільними відношеннями Р ₁ та Р ₂ невід’ємна, тобто d (P ₁, Р ₂) ³ 0, d (P ₁, Р ₂) = 0 тоді й лише тоді, коли Р ₁ = Р ₂.

АКСІОМА 2. (симетричності відстані). Відстань є симетричною величиною, тобто d (P ₁, Р ₂) = d (P ₂, Р ₁).

АКСІОМА 3. (трикутника). Для довільних відношень Р ₁, Р ₂, Р ₃ виконується нерівність d (Р ₁, Р ₃) £ d (Р ₁, Р ₂) + d (Р ₂, Р ₃) (нерівність трикутника). Рівність досягається, тоді коли відношення Р ₁, Р ₂, Р ₃ знаходяться «на одній прямій».

Формулювання аксіоми 3 вимагає введення аналогу прямої і поняття «знаходяться між» для відношень. Зробимо це для відношень типу ранжування, вважаючи, що ранжування подано за допомогою матриці .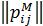

Вважатимемо, що ранжування Q лежить між ранжуваннями Р та R, якщо для всіх елементів матриць 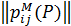, та виконано умову

Отже, у ранжуванні Q альтернатива х_i краща за х_j якщо хоча б в одному з ранжувань Р чи R альтернатива х_i краща за х_j. Альтернативи х_i та х_j можуть бути рівноцінні в ранжуванні Q, якщо вони рівноцінні чи протилежно впорядковані в Р та R. Будемо записувати [ Р, Q, R ], якщо ранжування Q знаходиться між Р й R.

Узагальнимо поняття прямої: будемо вважати, що ранжування Р ₁, Р ₂,..., Р_k розташовані на прямій, якщо для довільних Р_i, P_j, P_l, що належить цій множині ранжувань, [ Р_i, P_j, P_l ], де 1 £ і < j < l £ k, тобто

d (Р_i, P_l) = d (Р_i, P_j) + d (P_j, P_l).

АКСІОМА 4. (прямої). Якщо ранжування Q знаходиться між Р й R, тобто [ Р, Q, R ], то d (P, R) = d (P, Q) + d (Q, R).

АКСІОМА 5. (рівноправності альтернатив). Нехай F: А ® А – перестановка альтернатив. Якщо відношення P' і R' отримані з відношень Р та R перенумеруванням (перестановкою) альтернатив, то d (P, R) = d (P ', R '), тобто від перенумерування відстань між відношеннями не змінюється.

АКСІОМА 6. (відмінностей). Значення міри близькості між ранжуваннями Р та R залежить від тих сегментів цих ранжувань, у яких є відмінності в упорядкуванні альтернатив, тобто відстань між ідентичними сегментами ранжувань нульова.

Розглянемо два ранжування Р та R, які різняться лише впорядкуванням альтернатив, що займають місця з (r + 1)–го до (r + k)– го, (r + k) £ n, де n = саrd(A), тобто потужність множини–носія цих відношень у разі скінченної множини – це кількість альтернатив. Позначимо як Т (Р) й T (R) ранжування, отримані з Р й R відкиданням альтернатив, що займають місця від 1–го до r –го та від (r + k + 1)–го до n – го. Згідно з аксіомою 6, d (T (P), T (Q)) = d (P, Q).

АКСІОМА 7. (масштабу вимірювання). Мінімальна позитивна віддаль між ранжуваннями дорівнює 1.

Виявляється, що ці сім аксіом однозначно задають міру близькості на ранжуваннях. Для доведення цього твердження доведемо спочатку дві леми.

ЛЕМА 3.1. Якщо ранжування Р ₁, Р ₂,..., Р_k розташовані на прямій, то виконується співвідношення

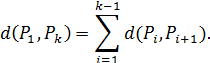
Доведення. Згідно з аксіомою 4, [ P_i, Р_{і +1}, Р_{і +2}] для всіх і від 1 до (k – 2), тобто d (Р_і, Р_{і +2}) = d (Р_і, Р_{і +1}) + d (Р_{і +1}, Р_{і +2}). Застосувавши цю аксіому (k – 2) разів, отримаємо потрібну рівність.

ЛЕМА 3.2. Для строгого ранжування Р аксіоми 1–7 однозначно задають віддалі d (P, Р ^–1) та d (P, 0), а саме d (P, Р ^–1) = n (n – 1), d (P, 0) = n (n – 1)/2, де n = card(A) (множина альтернатив скінченна, 0 – це ранжування, у якому всі альтернативи рівноцінні).

Доведення. Безпосередньо перевіривши аксіоми 1–7 для ранжувань двох альтернатив (n = 2) переконаємося, що міру близькості в цьому разі задано однозначно, і віддаль між протилежно впорядкованою парою альтернатив дорівнює 2, а між впорядкованою парою та парою рівноцінних альтернатив 1.

Побудуємо ланцюжок із ранжувань Р ₁, Р ₂,..., Р_k так, що Р ₁ = Р, Р_k = Р ^–1, а кожне ранжування Р_{і +1} відрізняється від Р_і заміною лише порядку альтернатив х_l та х_r, так що , тобто ця заміна наближає кожне наступне відношення до Р ^–1 водночас усе більше віддаляючи його від Р. Відповідно до леми 3.1 і аксіоми 6,

тобто відстань 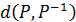визначено однозначно.

Щоб перейти від ранжування Р до Р ^–1 за умови, що загальна кількість альтернатив n = саrd(A), необхідно n (n – 1)/2 рази поміняти впорядкування двох альтернатив у ланцюжку Р ₁, Р ₂,..., Р_k, тобто k = n (n – 1)/2 + 1.

Узявши до уваги, що і кількість складових у сумі є (k – 1), одержимо рівність .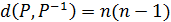

Для довільного строгого ранжування виконується умова [ Р, 0, Р ^–1]. Тоді, згідно з аксіомами 2, 4, 5 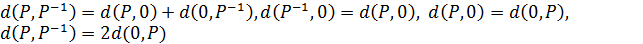, тобто .

Використовуючи аксіоми 1–7 і леми 3.1, 3.2 доведемо єдиність міри близькості на ранжуваннях.

Теорема 3.2. Аксіоми 1–7 визначають єдину (одну й лише одну) міру близькості на ранжуваннях.

Доведення. Доведемо теорему за індукцією. У разі n = 2 для довільних ранжувань Р_l і Р_r віддаль d (Р_l, Р_r) задано однозначно згідно з лемою 3.2. Нехай n = саrd(A) ³ 3. Якщо [ Р_l, 0, Р_r ], то за аксіомою 4 d (Р_l, Р_r) = d (Р_l, 0) + d (0, Р_r). У разі Р_r = 0 замінимо рівноцінні альтернативи на кожному кроці їх довільними строгими ранжуваннями, отримавши таким чином ланцюжок Р_r, Р_{r +1},..., Р_k, де Р_k – строге ранжування. Нуль (0) теж знаходиться на одній прямій із ранжуваннями Р_r, Р_{r +1},..., Р_k, і 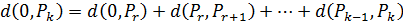. Для довільної пари (Р_i, Р_{i +1}) ранжувань цього ланцюжка ранжування T (Р_i) та T (Р_{i +1}) складаються з m < n альтернатив, які рівноцінні в Р_r, тобто віддаль d (T (P_i), T (Р_{i +1})) визначено однозначно, а отже, і d (P_i, Р_{і +1}) = d (T (P_i), T (Р_{i +1})) для всіх і Îє r, k – 1. За лемою 3.2, d (0, Р_k) = n (n – 1)/2, тому відстань d (0, Р_r) однозначно визначено як

Аналогічно визначається й віддаль d (Р_l, 0). Узявши до уваги, що d (Р_l, 0) = d (0, Р_l) та виконавши аналогічне доведення, одержимо, що відстань d (Р_l, P_r) = d (Р_l, 0) + d (0, P_r) для випадку, коли [ Р_l, 0, Р_r ] задано однозначно.

Нехай тепер ранжування 0 не знаходиться між Р_l і Р_r. Тоді в ранжуваннях Р_l та Р_r водночас знайдеться хоча б одна пара таких альтернатив х_i і х_j, що 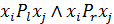. Побудуємо ранжування Р_{l +1}, яке відрізнятиметься від Р_l тим, що альтернативи гірші за х_i в ранжуванні Р_r, але кращі за х_i в ранжуванні Р_l, у ранжуванні Р_{l +1} також гірші за х_i. На наступному кроці побудуємо ранжування Р_{l +2}, яке відрізняється від Р_l тим, що в ньому гірші за х_i альтернативи впорядковано так само, як і в ранжуванні Р_r. Безпосередньою перевіркою виявимо, що ранжування [ Р_l, Р_{l +1}, Р_{l +2}, Р_r ] знаходиться на одній прямій, тобто d (Р_l, Р_r) = d (Р_l, Р_{l +1}) + d (Р_{l +1}, Р_{l +2}) + d (Р_{l +2}, Р_r). Ранжування T (Р_l) і T (Р_{l +1}) мають менше ніж n альтернатив, оскільки альтернатива х_j завідомо не належить до них за способом побудови. З аналогічних причин ранжування T (Р_{l +1}) та T (Р_{l +2}) не містять альтернативи х_i, а ранжування T (Р_{l +1}) та T (Р_r) – альтернативи х_j. За припущенням індукції, віддалі d (T (Р_l), T (Р_{l +1})), d (T (Р_{l +1}), T (Р_{l +2})), d (T (Р_{l +2}), T (Р_r)) визначені однозначно, тобто і в цьому разі однозначно визначено відстань d (Р_l, Р_r). Отже, аксіоми 1–7 визначають єдину міру близькості на ранжуваннях.

Визначимо формулу для визначення міри близькості між двома довільними ранжуваннями Р; і Рг згідно з аксіомами 1–7. Для цього доведемо таку теорему.

Теорема 3.3. Віддаль між двома довільними ранжуваннями Р_l та Р_u, що задовольняє аксіоми 1–7, визначається за формулою

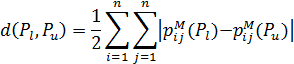
Доведення. Оскільки згідно з теоремою 3.2 метрика для ранжувань, що задовольняє аксіоми 1–7, єдина, потрібно довести, що наведена формула задовольняє ці аксіоми. Позаяк усі складові d (P_l, Р_u) невід’ємні, то аксіома 1 виконується. Крім того,

(справедлива аксіома 2 симетричності віддалі) та виконується нерівність трикутника

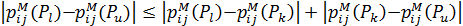
(справедлива аксіома 3). Якщо [ P_l, P_k, P_u ], то наведена вище нерівність перетворюється на рівність – виконується аксіома 4. Очевидно, що задовольняється аксіома 5. Якщо альтернатива х_k не належить до ранжувань Т (Р_u) та Т (Р_l), то p, унаслідок чого

Нехай I_s – множина індексів альтернатив, що належить до ранжувань Т (Р_l) і Т (Р_u). З огляду на попередню рівність отримаємо

чим і доведено, що виконується аксіома 6. Аксіома 7 також виконується, оскільки d (P_l, Р_u) = 1, коли ранжування P_l і Р_u відрізняються мінімально – упорядкуванням лише однієї пари альтернатив х_i й х_j, причому в одному з ранжувань х_i» х_j (альтернативи рівноцінні), а в іншому або 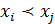. У всіх інших випадках (окрім тотожності) d (P_l, Р_u) ³ 2.

Віддаль між двома довільними ранжуваннями P_l і Р_u можна визначити лише за допомогою значень елементів матриць М (P_l) і М (Р_u), розміщених над головною діагоналлю, за формулою

Приклад 3.7. Два експерти проранжували п’ять альтернатив та виявили такий порядок їх важливості:

1. ;

2. .

Отже, перший експерт поставив на перше місце альтернативу х ₂, на друге – х ₅, третє–четверте місця поділили альтернативи х ₁ та х ₄, а останнє місце посіла альтернатива х ₃. Другий експерт натомість на перше та друге місця обрав альтернативи х ₂ й х ₃, третє – четверте місця в нього поділили альтернативи х ₁ та х ₅, а на останньому місці опинилась альтернатива х ₄. Побудуємо відповідні матриці відношень і .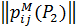

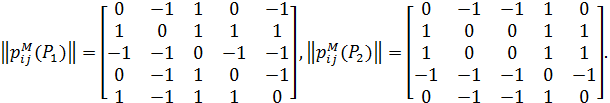
Віддаль між ранжуваннями Р ₁ та Р ₂ становить d (Р ₁, Р ₂) = 9. Побудуємо відношення Р_u, що лежить між Р ₁ та Р ₂, тобто [ Р ₁, Р_u, Р ₂]:

Віддалі d (Р ₁, Р_u) = 4, d (Р_u, Р ₂) = 5, d (Р ₁, Р ₂) = d (Р ₁, Р_u) + d (Р_u, Р ₂) = 4 + 5 = 9. Цьому відношенню відповідатиме ранжування .

Аналогічним чином як для ранжувань, доводиться існування єдиної міри й для еквівалентностей, при цьому аксіома 7 про мінімальну віддаль замінюється на аксіому про максимально можливу на множині еквівалентностей, а саме

max d (P_l, Р_u) = n (n – 1)/2,

і в цьому випадку міра розраховується за тією ж формулою, як і для ранжувань. Доведено також, що ця ж формула визначає міру близькості і на відношеннях порядку, толерантностей та довільних бінарних неметризованих відношеннях, представлених у вигляді матриці .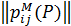

Приклад 3.8. Два експерти побудували наступні еквівалентності.

1. {(х ₁, х ₅); (х ₂, х ₃); (х ₂, х ₄); (х ₃, х ₄)}.

2. {(х ₁, х ₃); (х ₂, х ₅)}.

Їм відповідають матриці

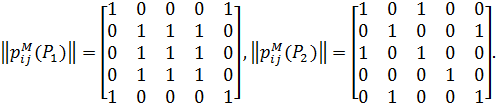
Значення міри близькості для цих відношень становить d (P ₁, Р ₂) = 6.

Приклад 3.9. Нехай задано два відношення часткового порядку:

Р ₁ = {(х ₁, х ₂); (х ₁, х ₃); (х ₁, х ₄); (х ₁, х ₅); (х ₂, х ₄); (х ₂, х ₅)},

P ₂ = {(х ₃, х ₁); (х ₃, х ₂); (х ₃, х ₄); (х ₃, х ₅)}

Побудуємо відповідні матриці відношень:

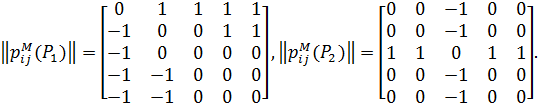
Значення міри близькості для цих відношень становить d (P ₁, Р ₂) = 10.

Приклад 3.10. Два експерти надали такі відношення толерантності:

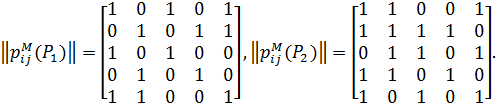
Значення міри близькості для них становить d (P ₁, Р ₂) = 5.

Приклад 3.11. Два експерти порівнювали попарно та зазначали альтернативи, які, на їхню думку, мали перевагу. У результаті було побудовано такі матриці відношень:

Значення міри близькості для цих відношень становить d (P ₁, Р ₂) = 12.

Отже, для неметризованих відношень відстань між відношеннями Р_l і Р_k залежить від ступеня розбіжностей між відповідними матрицями відношень і . Однак зрозуміло, що оскільки матриці неметризованих відношень, узагалі кажучи, не мають метричної інтерпретації, то їх елементами можуть бути не обов’язково 1 й 0, але й довільні елементи.

Дата добавления: 2014-01-05