Сжимаемость

Способность жидкости или газа под действием внешнего давления изменять свой объем и, следовательно, плотность, называется сжимаемостью. Сжимаемость жидкости характеризуется коэффициентом объемного сжатия (сжимаемости) b _с, м²/Н, представляющим относительное изменение объема жидкости V, м³, при изменении давления р, Па, на единицу:

.

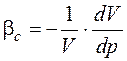Знак минус в формуле указывает, что при увеличении давления объем жидкости уменьшается.

Величина, обратная коэффициенту объемного сжатия – модуль упругости жидкости:

.

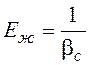При относительно невысоких давлениях сжимаемостью жидкостей пренебрегают. При значительных изменениях давления сжимаемость капельных жидкостей следует учитывать.

Вследствие большой сжимаемости газообразных жидкостей их плотность и удельный вес в значительной степени зависят от температуры и давления.

Процессы сжатия и расширения газов подчиняются известным из физики законам Бойля – Мариотта и Гей – Люссака для идеальных газов.

Сжимаемость воды весьма незначительна, при увеличении давления на 9,8 МПа (на 100 атмосфер) объем воды уменьшается на 1/20000 первоначального объема.

Условия работы гидротехнических сооружений позволяют считать воду несжимаемой средой. Но не следует забывать, что такое допущение правомерно лишь в тех случаях, когда изменения давления невелики. Так, сжимаемость воды существенно сказывается на положении уровня водной поверхности Мирового океана. Если бы вода была абсолютно несжимаема, то отметки уровня воды в океанах поднялись бы примерно на 30 м.

Вязкость

Вязкость – свойство жидкости оказывать сопротивление относительному сдвигу слоев. Вязкость проявляется в том, что при относительном перемещении слоев жидкости на поверхностях их соприкосновения возникают силы сопротивления сдвигу Т, называемые силами внутреннего трения, или силами вязкости (рис. 1.2). Благодаря этим силам медленнее движущийся слой жидкости «тормозит» соседний слой, движущийся быстрее, и наоборот. Силы внутреннего трения появляются вследствие наличия межмолекулярных связей между движущимися слоями.

Наличие сил вязкости в движущейся жидкости подтверждается простым и наглядным опытом. Если в цилиндрическую емкость, заполненную жидкостью опустить вращающийся цилиндр, то вскоре придет в движение (начнет вращаться вокруг своей оси в том же направлении, что и вращающийся цилиндр) и сама емкость с жидкостью. Этот факт свидетельствует о том, что вращательный момент от вращающегося цилиндра был передан через вязкую жидкость самой емкости, заполненной жидкостью.

Вязкость проявляется для большинства жидкостей только при движении. Но у некоторых жидкостей, например нефтепродуктов, смазочных масел при низких температурах, коллоидных растворов и в состоянии покоя имеются силы трения. Такие жидкости называются аномальными (неньютоновскими).

Представим на продольном разрезе потока (рис. 1.2) некоторое живое сечение АВ и соответствующую ему эпюру скоростей АВС. Покажем далее два слоя жидкости (заштрихованы на чертеже), из которых первый слой движется со скоростью u ₁, а второй – со скоростью u ₂. Поверхность соприкосновения 1-1 этих жидких слоев имеет площадь S. По этой поверхности (вдоль нее) в вязкой жидкости развиваются парные силы внутреннего трения: Т ₁, приложенная к первому слою со стороны второго, и Т ₂, приложенная ко второму слою со стороны первого. Очевидно,

,

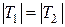причем первый слой жидкости, движущийся с большей скоростью, за счет трения по поверхности 1-1 способствует ускорению движения второго слоя; второй же слой, наоборот, благодаря трению тормозит первый слой.

Законы продольного внутреннего трения были установлены Ньютоном в 1686 г.

Эти законы можно сформулировать так:

Сила Т продольного внутреннего трения в параллельноструйном потоке жидкости, то есть сила трения, возникающая при скольжении отдельных прямолинейных слоев жидкости друг по другу:

1) прямо пропорциональна так называемому градиенту скорости;

2) прямо пропорциональна площади S поверхности соприкасания данных слоев жидкости;

3) не зависит от давления;

4) зависит от физических свойств жидкости (от рода жидкости), а следовательно, и от ее температуры.

Положения 1, 2 и 3 отличаются от соответствующих законов, относящихся к твердым телам: в случае твердых тел сила трения, как известно, зависит от нормального давления и практически не зависит от скорости движения тела, а также от площади S. Законы Ньютона можно представить в аналитической форме:

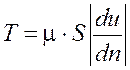, (1.1)

где m – некоторый коэффициент пропорциональности, называемый, как отмечалось выше, динамическим коэффициентом вязкости или просто коэффициентом вязкости. Величина m зависит от рода жидкости, а также от ее температуры; чтобы подчеркнуть это обстоятельство, иногда m называют коэффициентом молекулярной или физической вязкости. Численные значения m для различных жидкостей находятся опытным путем при помощи особых приборов, называемых вискозиметрами;

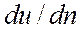– градиент скорости, то есть производная от величины скорости и по нормали п, проведенной к поверхности 1-1 соприкасания слоев жидкости. Если толщина выделенных на рис. 1.2 слоев жидкости бесконечно мала, то для отмеченных на чертеже величин dи и dп можем написать:

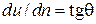, (1.2)

где q – угол, образованный вертикалью и касательной к кривой ВС эпюры скоростей в точке, лежащей на линии 1-1.

Именно соотношением (1.2) и выражается градиент скорости, входящий в формулу (1.1). Величина 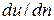в зависимости от выбранного направления n (см. на рис. 1.2 направления п ₁ и п ₂) может быть как положительной, так и отрицательной. С тем, чтобы в формуле (1.1) величину Т получать всегда положительной, в эту формулу введено абсолютное значение градиента скорости.

Обратим внимание, что при равномерном распределении скоростей по живому сечению, то есть в случае, когда 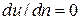, силы внутреннего трения в вязкой жидкости согласно (1.1) отсутствуют.

Формула (1.1), предложенная Ньютоном вначале в качестве гипотезы и подвергавшаяся в дальнейшем тщательной опытной проверке, в настоящее время общепринята для расчета касательных напряжений при ламинарном течении жидкостей.

Ламинарным, то есть слоистым, называется течение вязкой жидкости, при котором отсутствует перемешивание между ее слоями. Неупорядоченное движение вязкой жидкости с интенсивным перемешиванием частиц называется турбулентным. В случае турбулентного течения формула Ньютона неприменима.

Касательные напряжения продольного внутреннего трения для ламинарного режима при прямолинейном движении представятся в соответствии с (1.1) зависимостью:

.

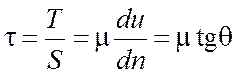Следовательно, динамический коэффициент вязкости равен:

.

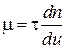Отсюда находим размерность динамического коэффициента вязкости:

В системе СИ динамическая вязкость измеряется в 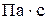. Единицу, равную 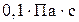, называют пуазом (П) по имени профессора Пуазейля, впервые получившего точные опытные данные о вязкости.

Физический смысл динамического коэффициента вязкости виден из рассмотрения единиц его измерения: в числителе – работа, а в знаменателе – объемный расход:

.

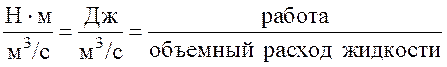Таким образом, динамический коэффициент вязкости представляет собой работу, которую необходимо совершить при относительном течении слоев жидкости для единицы объемного расхода.

В гидравлических расчетах кроме динамической вязкости широко используется кинематическая вязкость, равная отношению динамической вязкости к плотности жидкости:

.

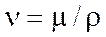Отсюда находим размерность кинематической вязкости:

.

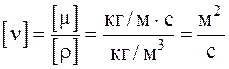Название «кинематическая вязкость» отражает тот факт, что в размерность входят только кинематические величины. В системе СИ – м²/с.

Физический смысл кинематического коэффициента вязкости также виден из единиц его измерения:

.

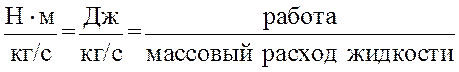Следовательно, кинематический коэффициент вязкости представляет собой работу, которую необходимо совершить при относительном движении слоев жидкости для единиц массового расхода.

Вязкость капельных жидкостей зависит от температуры и уменьшается с увеличением последней. Вязкость газов, наоборот, с увеличением температуры возрастает. Это объясняется различием самой природы вязкости в жидкостях и в газах. В жидкостях молекулы расположены гораздо ближе друг к другу, чем в газах, и вязкость вызывается силами молекулярного сцепления. Эти силы с ростом температуры уменьшаются, поэтому вязкость падает. В газах же вязкость обусловлена главным образом беспорядочным тепловым движением молекул, интенсивность которого увеличивается с температурой.

Вязкость капельных жидкостей зависит также от давления, однако эта зависимость существенно проявляется лишь при относительно больших изменениях давления, порядка нескольких сотен атмосфер. С увеличением давления вязкость большинства жидкостей возрастает, но при давлениях меньше 10 МПа изменением вязкости обычно пренебрегают.

Вязкость газов при обычно встречающихся в технике перепадах давления не зависит от давления. Но если газы подвергаются очень сильному сжатию, их вязкость значительно возрастает.

Вязкость жидкостей измеряют с помощью приборов – вискозиметров различных типов.

Поверхностное натяжение (капиллярность)

Известно, что молекулы жидкости, находящиеся на границе с газом, твердым телом или между двумя несмешивающимися жидкостями, находятся под воздействием сил взаимного притяжения. Вследствие этого вся свободная поверхность жидкости находится в состоянии равномерного поверхностного натяжения s. Под влиянием поверхностного натяжения поверхность жидкости стремится принять форму, соответствующую наименьшей площади. Малые массы жидкости в воздухе стремятся к шарообразной форме, образуя капли.

Влияние поверхностного натяжения необходимо учитывать при изучении потоков с малой глубиной, при захвате окружающего воздуха движущейся жидкостью (аэрация жидкости), в капиллярах и т.д.

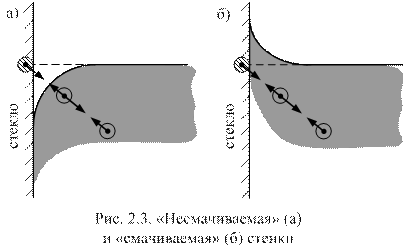В трубках малого диаметра наблюдается подъем или опускание жидкости относительно нормального уровня, а также искривление сво­бодной поверхности. Обратимся к рассмотрению жидкости в капиллярной трубке. Как видно из рис. 2.3, в районе примыкания поверхности жидкости к стенке трубки можем получить одну из следующих картин:

– если взаимное притяжение двух молекул жидкости велико по сравнению с притяжением молекул жидкости к частице твердой стенки, то получаем схему, изображенную на рис. 2.3, а (случай «несмачиваемой стенки»);

– если взаимное притяжение двух молекул жидкости мало по сравнению с притяжением молекул жидкости к частице твердой стенки, то получаем схему, изображенную на рис. 2.3, б (случай «смачиваемой стенки»).

Высота подъема смачивающей жидкости (или опускание несмачивающей жидкости) в стеклянной трубке диаметром d определяется по формуле для полусферического мениска:

,

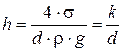где k имеет следующие значения: для воды k = 30 мм²; для ртути
k = –10,1 мм²; для спирта k = 11,5 мм².

Величина напряжений на границе раздела зависит от температуры жидкости; при увеличении температуры внутренняя энергия молекул возрастает, уменьшается напряжение в пограничном слое жидкости и, следовательно, уменьшаются силы поверхностного натяжения.

Дата добавления: 2014-01-05