Способи доведення теорем (дедуктивний, індуктивний, метод від супротивного тощо)

2. Спочатку зазначимо, що довести теорему – це означає встановити логічним шляхом, що завжди, коли виконується властивість А(х) буде виконуватись і властивість В(х). Доведення теорем в математиці проводиться за правилом логіки без будь-яких посилань на наочність та досвід. У математиці існують різні способи доведення теорем, які класифікують по-різному. Серед різних способів доведення теорем зупинимося на характеристиці тих, які найчастіше зустрічаються в шкільному курсі математики. У першу чергу вкажемо на дедуктивний спосіб доведення теорем, сутність якого полягає в тому, що виходячи з умови теореми і використовуючи доведені раніше теореми, ми будуємо ланцюжок міркувань, який дозволяє нам переконатися в справедливості висновків теорем. Покажемо це на прикладі такої теореми «Сума внутрішніх кутів довільного трикутника дорівнює 180°».

Доведення: беремо довільний трикутник (див. малюнок № 2.1.) і проводимо через його вершину пряму, паралельну протилежній стороні (це можна зробити, оскільки доведено, що через точку, поза прямою можна провести пряму, паралельну даній). <1+<2+<3=180°, як сума кутів, які утворюють розгорнутий кут. <1=<4 – як внутрішні різносторонні при паралельних прямих та січній. Аналогічно <3=<5. Тоді рівність <1+<2+<3=180° перетвориться у рівність <4+<2+<5=180°. Отже, сума внутрішніх кутів трикутника дорівнює 180°. Теорему доведено.

Сутність індуктивних доведень полягає в тому, що на основі розглянутих кількох окремих випадків ми робимо загальний висновок. Для того, щоб не розглядати всі часткові випадки, в математиці є метод доведення, який називається методом математичної індукції. Він складається з таких етапів: а) перевіряємо твердження для n=1; б) припускаємо істинність твердження при n=k; в) виходячи з припущення пробуємо довести істинність твердження при n=k+1. Тоді дане твердження буде справедливим для будь-якого натурального числа. Проілюструємо сказане на такому прикладі: довести, що добуток двох послідовних натуральних чисел ділиться націло на 2.

Доведення:

1. Перевіримо справедливість твердження для будь-якої пари послідовних натуральних чисел. Дійсно, добуток 1•2=2, а 2 кратне 2. Отже, для n=1 і n=2 твердження справедливе.

2. Припустимо, що твердження справедливе для будь-якої пари послідовних натуральних чисел n і n+1, тобто n(n+1)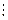2.

3. Спробуємо довести справедливість твердження для n=k+1. Утворимо добуток (n+1)(n+2) і розкриємо другу дужку. Отримуємо (n+1)n+2(n+1). У цій сумі перший доданок (n+1)n ділиться націло на 2 згідно припущення, а другий доданок 2(n+1) ділиться націло на 2 згідно теореми про подільність добутку. Таким чином, кожен доданок суми ділиться на 2, а тому і сума (n+1)n+2(n+1)=(n+1)(n+2) поділиться націло на 2. Отже, теорему доведено.

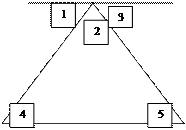Малюнок № 2.1.

Наступним способом доведень є спосіб доведення від супротивного, сутність якого полягає в тому, що ми заперечуємо висновок теореми і пробуємо це довести. В результаті ми приходимо до суперечності із умовою теореми або з доведеним раніше твердженням. Найбільш часто цей спосіб доведення використовують при доведенні теорем єдиності. Покажемо це на такому прикладі: якщо різниця двох дійсних чисел існує, то вона єдина.

Доведення: нехай нам дано два дійсних числа а,вєR. Згідно означення різниці число а-в=сєR. Припустимо, що різниця двох дійсних чисел не єдина. Нехай існують дві різних різниці, тобто: а-b=с₁ і а-b=с₂, причому с₁≠с₂. Звідси маємо а=b+с₁ і а=b+с₂, тобто b+с₁=b+с₂, а тепер с₁=с₂, що суперечить вибору чисел с₁ і с₂. Ця суперечність говорить, що наше припущення про неєдиність різниці було хибним. Таким чином, якщо різниця існує, то вона єдина. Теорему доведено.

Дата добавления: 2014-01-05