Принцип резолюций

B сущности, в основе принципа лежит несложная схема рассуждений. Пусть А, B и С - формулы и имеются два дизъюнкта:

1. (А + С) и 2. (B +^Ø С),

которые мы будем считать истинными. Положим теперь, что С = И.

Подставив это значение в первое выражение, получим дизъюнкт вида А + И, который истинен при любом А. Подставив С = И во второе выражение, получим дизъюнкт B + Л, из которого однозначно следует, что B = И, поскольку принято, что весь дизъюнкт истинен.

Положим теперь С = Л. Второй дизъюнкт истинен при любом B, но первый принимает вид А + Л, откуда следует, что А = И.

Все это означает, что, независимо от интерпретации формулы С, либо А, либо B истинны. Это можно отразить в виде нового дизъюнкта (А + B), исключив контрарные формулы С и .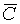

Другими словами, выполняется правило

(А + C, B + 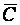) 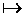(A + B). (5.12)

Правило особенно эффективно, если А и B дизъюнкты, а С - высказывание. Это правило называется правилом резолюции, а вновь полученный дизъюнкт - резольвентой. Он формируется как "сумма" оставшихся формул, за исключением контрарных, т.е. разных по знаку.

Для дизъюнктов (p + q + 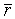) и (m + r), например, резольвента будет иметь вид (p + q + m). Для дизъюнктов (p + r) и (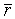) соответственно (p), а вот в случае (p) и (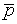) обе литеры "уничтожаются". Это пример получения пустого дизъюнкта. Еще один пример. Имеются два дизъюнкта ( 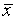+ y) и (x + 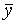). Получаемые здесь резольвенты (x + 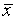) или (y + 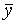) равны 1, информации не несут, их следует отбрасывать.

B логическом плане каждый полученный дизъюнкт - резольвента равносилен обоим дизъюнктам-родителям, участвовавшим в резолюции, (они так и называются - родители). Он становится очередной гипотезой и участвует в резолюции на равных с другими. Это касается и пустого дизъюнкта, но будучи поставлен в ряд гипотез Нi, он делает формулу типа (5.10) равной 0, что и является ее доказательством.

Пример. Доказать невыполнимость множества дизъюнктов:

H = (p + q, p + r, 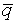+ 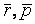). Пронумеруем гипотезы:

1. p + q,

2. p + r,

3. ,

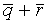4. .

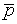Далее применяется правило резолюции. Полученные резольвенты присоединяются к исходному множеству, с ними снова можно проводить резолюции. Ниже следует список резольвент, в скобках указываются номера резольвент, участвовавших в резолюции.

5. q (1,4),

6. r (2,4),

7.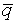 (3,6),

8. Л (5,7).

Надо отметить, что выбранный путь порождения резольвент может быть не единственным. Например, в нашем случае, результат можно было получить чуть быстрее, если пойти по следующему пути:

5. p + 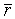(1,3),

6. p (2,5),

7. Л (4,6).

Как видно из примера, метод резолюций легко представим в виде несложного регулярного алгоритма. Это предопределяет успешное применение ЭВМ в решении задач вывода, хотя здесь и возможны неожиданные трудности. Дело в том, что машина ищет резолюцию слепо, методом перебора. При таком поиске путь к результату может быть весьма долгим. Возможны случаи простого зацикливания машины. Простейший пример: имеется два дизъюнкта p и 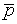+ q. При машинной реализации резольвента q может порождаться неограниченное число раз. Предусматривая подобные случаи, применяют специальные стратегии поиска резольвент и соответствующее программирование. Некоторые такие стратегии мы рассмотрим в следующем разделе.

В заключение отметим такое важное обстоятельство:

множество резольвент (вместе с родительскими дизъюнктами) образует не что иное как математическую модель некоторой предметной области. Каждая новая резольвента добавляет новое состояние в пространство состояний Мпо, а поиск решения в пространстве состояний представлен операцией логического вывода.

Дата добавления: 2014-01-05