Числові вирази та їх види. Значення числового виразу та порядок обчислення значень числового виразу

МОДУЛЬ 6.: «ВИРАЗИ. РІВНЯННЯ. НЕРІВНОСТІ. ФУНКЦІЇ».

Множина дійсних чисел та її властивості.

Розв’язання.

Оскільки Ö3=1,7320508… і Ö2=1,4142135…, то знайдемо десяткові наближення цих чисел з точністю до сотих. Маємо 1,73≤Ö3≤1,74 і 1,41≤Ö2≤1,42. Тоді 1,73:1,42≤Ö3:Ö2≤1,74:1,41. Отже, 1,21≤Ö3:Ö2≤1,23. Випадки а) і б) пропонуємо студентам розглянути самостійно.

6. Означення: об’єднання множини раціональних чисел та множини додатних і від’ємних ірраціональних чисел називають множиною дійсних чисел.

Основними властивостями цієї множини є наступні.

Властивість 1: множина дійсних чисел впорядкована.

Властивість 2: множина дійсних чисел незчисленна.

Властивість 3: множина дійсних чисел замкнена відносно операцій додавання, віднімання, множення та ділення, крім ділення на нуль.

Властивість 4: між множиною дійсних чисел і множиною точок числової прямої існує взаємно однозначна відповідність.

Означення: говорять, що множина А має потужність континууму, якщо вона еквівалентна множині дійсних чисел R.

У математиці доведено, що будь-який числовий проміжок числової прямої є множиною потужності континууму.

Запитання для самоконтролю та самостійної роботи студентів за модулем У.

1. Сформулювати теорему про існування та єдиність операції додавання у множині цілих чисел.

2. Сформулювати теореми, які виражають закони, яким підкоряється операція додавання у множині цілих чисел.

3. Сформулювати теорему про існування та єдиність операції віднімання у множині цілих чисел.

4. Сформулювати теорему про існування та єдиність операції множення у множині цілих чисел.

5. Сформулювати теореми, які виражають комутативний, асоціативний та дистрибутивний закони, яким підкоряється операція множення у множині цілих чисел.

6. Довести самостійно другу частину теореми, яка виражає основну властивість дробу.

7. Довести самостійно комутативний закон додавання невід’ємних раціональних чисел.

8. Довести методом від супротивного теорему про єдиність різниці невід’ємних раціональних чисел.

9. Довести самостійно комутативний закон множення невід’ємних раціональних чисел.

Змістовний модуль 6.1. «Вирази.».

ПЛАН.

1. Числові вирази та їх види. Значення числового виразу та порядок обчислення значень числового виразу.

2. Числові рівності та нерівності, їх властивості.

3. Вираз із змінною та його область визначення.

4. Тотожні перетворення виразів. Тотожності. Виведення основних тотожностей.

ЛІТЕРАТУРА: [1] – с. 238-293, 317-384; [2] – с. 53-59, 110-115, 294-355; [3] – с. 118-127.

1. У математиці під числовою алгеброю розуміють таку алгебру, основою множиною якої є числа і букви (під якими розуміють числа), основними операціями якої є додавання, віднімання, множення і ділення. З елементів основної множини за допомогою операцій утворюють інші елементи числової алгебри, а за допомогою основних операцій визначають інші нові операції, вводячи для них нові позначення.

Мова будь-якої алгебри складається з множини знаків, яку називають алфавітом цієї мови. Числова алгебра містить десять букв, які прийнято називати цифрами: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. За допомогою цифр згідно з певними правилами утворюються назви будь-яких чисел. Для позначення числових змінних використовують букви латинського алфавіту a, b, c, …, x, y, z або деякі з цих букв з індексами 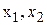... Інколи букви латинського алфавіту використовуються і для позначення числових сталих, тобто для позначення назв чисел. Для позначення певного конкретного, але не важливо якого числа, використовуються початкові букви латинського алфавіту a, b, c, …, а останніми буквами латинського алфавіту позначають змінні.

Для позначення операцій використовують відомі знаки „+”, „-”, „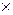”, „:”, а крім цього для запису чисел можуть використовувати праву „(” і ліву „)” дужки. Таким чином, алфавіт мови, на якій описується будь-яка числова алгебра, повинен включати таку множину: А={0, 1, 2, 3, 4, 5, 6, 7, 8, 9, +. -, ´, ·,:, (,)}. Із елементів множини А утворюють скінченні послідовності цифр і букв, які називають виразами. Однак, так само як і в українській мові, не кожна послідовність цифр і букв алфавіту А утворює вираз. Наприклад, послідовність 5-) не є виразом. Саме тому постає питання про визначення поняття „вираз”. Хоча це поняття є одним з основних понять математики, зазначимо, що не існує загальноприйнятого означення поняття „вираз”. Саме тому наведемо індуктивне означення поняття „вираз”, в якому: 1) перераховуються елементарні вирази; 2) формулюються правила утворення нових виразів, із тих, що вже є; 3) стверджується, що інших виразів, крім тих, які можуть бути утворені у відповідності з першими двома пунктами визначення, не існує.

Означення: 1. Кожна окрема цифра або буква латинського алфавіту є виразом. Такі вирази називаються елементарними. 2. Якщо і вирази, то і – також вирази. 3. Інших виразів, крім тих, які можуть бути одержані у відповідності з пп. 1.2, не існує.

Для спрощення запису виразів прийняли такі домовленості:

а) опускати зовнішні дужки, які містять всередині себе всі решта букв, які складають вираз;

б) у виразі повинна бути однаковою кількість правих і лівих дужок;

в) вважати, що знак множення пов’язує сильніше, ніж знак додавання.

Наведене означення виразу та прийняті домовленості щодо правил запису виразів дозволяють відносно будь-якої послідовності цифр чи букв встановити чи є вона виразом, чи ні. Покажемо це на наступному прикладі.

Вправа: встановити чи є виразами такі послідовності букв: 1) (((3+b)●3))+(4●у)); 2) (((7+а)●3+(8●а)).

Розв’язання:

Перевіряємо, чи є у послідовностях зовнішні дужки, які містять всередині себе весь запис. Отже, у кожному з наведених записів слід опустити по одній зовнішній дужці. Оскільки у першому виразі є 4 лівих і 5 правих дужок, то такий запис не є виразом, бо не виконується друга домовленість. Аналогічно і другий запис не є виразом. Відповідно до третьої вимоги, слід опустити дужки, в яких стоїть лише дія множення. Таким чином, для того, щоб вказані записи були виразами, записи слід представити так: 1) (3+b)●3+4●у; 2) (7+а)●3+8●а.

У математиці існують різні класифікації виразів. Відповідно до однієї з них всі вирази поділяють на числові та нечислові. Щоб зрозуміти цю класифікацію приймемо наступне означення.

Дата добавления: 2014-01-05