Методы теоретико-группового анализа колебательных спектров

После правильного выбора элементарной (примитивной) ячейки и базиса решетки необходимо установить расположение элементов симметрии в структуре и построить полное колебательное представление

Так как элементарная (примитивная) ячейка кристалла включает все неэквивалентные атомы (базис ячейки), то, чтобы определить фундаментальные колебания достаточно проанализировать колебания атомов в одной элементарной ячейке.

Однако, так как вид нормальных координат заранее не известен и их нахождение связано со значительными трудностями, то наиболее простым методом анализа колебательного спектра является теоретико-групповой.

При этом следует учитывать, что фундаментальные колебания соответствуют колебаниям подрешеток эквивалентных атомов друг относительно друга. Среди этих колебаний три описывают синфазное движение всех подрешеток, т. е. движение кристалла, как целого. Это, так называемые, акустические моды и остальные 3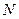-3 – оптические моды.

При этом необходимо учитывать сложности выбора элементарной (примитивной) ячейки. Наиболее полно фундаментальные колебания характеризует ячейка Вингера-Зейтца для обратной решетки(пространства волновых векторов ), называемой зоной Бриллюэна.

Классификация производится по неприводимым представлениям пространственной группы волнового вектора , которая является подгруппой пространственной группы кристалла .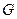

Чтобы определить количество независимых волн с одним и тем же волновым вектором 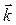, надо знать сколько раз неприводимое представление группы трансляций, соответствующее этому значению 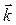, содержится в полном колебательном представлении, которое реализуется на всех смещениях .

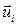Преобразование связывает составляющие смещений только эквивалентных атомов в различных ячейках кристалла. Если число атомов в ячейке равно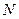, то все многообразие смещений {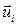} можно разбить на 3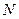многообразий, на каждом из них будет реализоваться регулярное представление группы трансляций.

Так как неприводимые представления группы трансляций одномерны, то в регулярном представлении они могут встретиться лишь по одному разу. Поэтому в полном колебательном представлении каждое неприводимое представление будет содержаться точно 3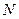раз.

Число различных нормальных колебаний или число различных плоских волн с одним и тем же волновым вектором 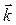всегда равно 3.

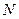Поскольку операции трансляции решетки действуют на предельные колебания подобно операции тождественного преобразования, эти операции из рассмотрения можно исключить.

Тогда общий метод анализа симметрии колебаний будет состоять в следующем: при 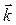=0 группа волнового вектора тождественна пространственной группе кристалла, т.е. 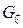=G. Представление G разлогаем на комплексы по инвариантной подгруппе трансляций :

.

Каждый комплекс является элементом фактор-группы G/. Фактор-группа изоморфна точечной группе, определяющей класс, к которому принадлежит данный кристалл.

Если пространственная группа решетки задана, то известна и таблица ее характеров, и неприводимые представления точечной группы, изоморфной своей фактор-группе. Данное неприводимое представление Г^(a) содержится в приводимом Г представлении n^(a) раз согласно формуле разложения:

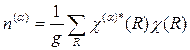, (2.43)

где g – порядок точечной группы кристалла; R – операция из фактор-группы; c^(a)® и c® – характеры, связанные с операцией R группы в представлениях Г^(a) и Г.

При этом c® вычисляется по формулам

, (2.44)

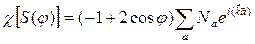, (2.45)

Где N_a – число атомов нулевой ячейки, переходящих при операции R в ячейку с вектором .

Таким образом, нормальные колебания кристалла классифицируются с помощью волнового вектора 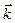, лежащего в первой (приведенной) зоне Бриллюэна. Каждому вектору 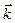соответствует 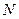нормальных координат, (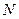- базис элементарной ячейки). Нормальные координаты, преобразующиеся по одному и тому же неприводимому представлению точечной группы имеют одинаковую частоту. Такую же частоту имеют соответствующие нормальные координаты (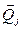), принадлежащие другим векторам (лучам) звезды вектора 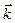. Изложенное справедливо для кристаллов, имеющих симморфные пространственные группы.

Для несимморфных групп классификация нормальных координат (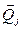) производится по неприводимым представлениям не точечной группы, а пространственной группы волнового вектора .

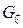Обычно фундаментальные колебаний 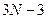оптические и 3 акустические моды анализируются отдельно по формулам:

; =, =,

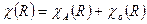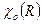где , 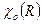- характеры представления акустических и оптических мод, «+» соответствует оператору симметрии повороту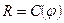, а «-» оператору симметрии зеркального поворота - .

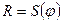При теоретико-групповом анализе колебаний кристалла необходимо учитывать:

точечную группу симметрии нейтральной или ионной молекулы в свободном состоянии;

пространственную группу симметрии кристалла;

число формульных единиц молекул (ионов) в элементарной ячейке;

Дата добавления: 2014-01-05