Лекция 6. Течение вязких жидкостей в цилиндрическом и плоском каналах

Рассмотрим течение расплава полимера под действием перепада давления вдоль оси канала с радиусом R а сравнительно большой длиной l. Давление на входе в канал равно p, а на выходе p₀. Так как течение установившееся, то принимаем, что =const (рис. 6.1), т. е. начальный входной участок канала не рассматривается.

Перепады давлений по другим координатам равны нулю:

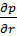= = 0

Соответственно скорости и напряжения сдвига также равны нулю:

_r = _Θ = 0; τ_rΘ = 0; τ_Θz = 0

Для решения принимаем следующие допущения:

1) Вязкость расплава не изменяется во времени; 2) скольжение на стенках канала отсутствует, т.е. при r = Rν_z = 0; 3) нормальные напряжения при течении остаются постоянными:

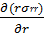= 0; 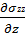= 0; = 0

4) гравитационные силы не учитываем, так как они намного меньше сил, обусловленных напряжением сдвига, поэтому:

ρg_r = ρg_Θ = ρg_z = 0

5)инерционные силы равны нулю:

ρ = ρ = ρ = 0

Рассмотрим произвольный элемент жидкости, расположенный внутри цилиндрической поверхности, и запишем для него уравнение движения.

Проекция на направление r:

ρ( + + 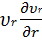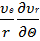- + 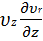) = (6.1)

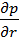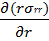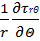- + ( + - + ) + ρg_r

Проекция на направление :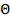

ρ( 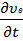+ + 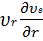- + 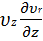) = (6.2)

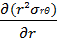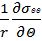- + ( + + ) + ρg

Проекция на направление r:

ρ( + + - + 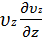) = (6.3)

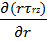- + ( + + ) + ρg_z

Если проанализировать уравнения (6.1) и (6.2) с учетом принятых условий и допущений, то видно, что все члены этих уравнений равны нулю, а из уравнения (6.3) можем записать:

=

Поскольку = const, то последнее уравнение можно преобразовать в обычное дифференциальное уравнение:

= r

Интегрируя последнее выражение, находим:

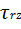= + (6.4)

На стенках канала скорость равна нулю, а в центре при = 0 она максимальна. Следовательно, вследствие симметрии потока на равных расстояниях от оси скорости также будут равны, поэтому в центре канала отсутствует скорость сдвига = 0 и = 0. Подставив в уравнение (6.4) = 0 и 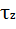= 0, находим 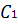= 0, тогда:

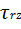= (6.5)

Эпюра распределения напряжений показана на рис. 6.1. Максимальное значение напряжения будет на стенке канала при r = R. Для установившегося потока, когда

= = -

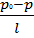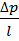
напряжение сдвига на стенке канала равно:

= - (6.6)

Знак минус указывает на то, что напряжения сдвига направлены в сторону, противоположную направлению оси z.

Для нахождения скорости потока воспользуемся реологическим уравнением (5.3), в которое вместо вязкости подставим степенное уравнение (5.7). С учетом принятых условий и допущений, все члены уравнения (5.6), кроме 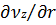, равны нулю. Поэтому в окончательном виде после подстановки уравнений (5.6) и (5.7) в уравнение (5.3) имеем:

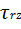= K( )ⁿ

Подставив это значение 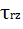в уравнение (6.5), из нового равенства находим:

d 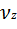= ( )^1/nr^1/ndr

Интегрируя это уравнение по r, получаем:

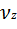= ( ) ^1/n r^(1+n)/n+ C₂

Из условия прилипания расплава к стенкам канала следует, что r = R, 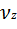= 0, тогда:

C₂ = - ( )^1/n R^(1+n)/n

Подставим вместо С₂ его значение, получаем:

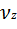= [1 – (r/R)^(1+n)/n] (6.7)

Здесь

= - ( )^1/n R (6.8)

Уравнение (6.7) при r = 0 приводится к выражению (6.8), т.е. 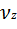– или 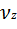равна максимальной скорости потока.

Взяв в сечении канала элементарное кольцо с радиусом r и толщиной dr, находим его площадь:

S = 2πrdr

Обычно расход расплава V равен произведению площади сечения канала на скорость потока. Для полного сечения:

V = 2π rdr

Подставив вместо 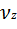его значение из (6.7), получаем:

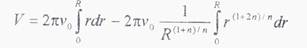
После интегрирования и преобразований получаем уравнение расхода расплава:

V = 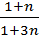π 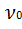R² (6.9)

Для нахождения скорости сдвига продифференцируем уравнение (6.7):

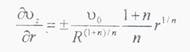
Заменив в этом выражении значением, найденным из уравнения (6.9)

= πR²,

получаем:

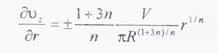
Скорость сдвига на стенке канала при r = R равна:

Если в уравнение подставить n = 1, то получаем скорость сдвига для потока ньютоновской жидкости:

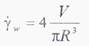
Рассмотрим движение в щелевом канале, образованном двумя пластинами шириной B и длиной l, расстояние между которыми H (рис. 6.2). Течение осуществляется вдоль оси z под действием перепада давления, при этом =const.

Так как градиенты давлений равны нулю, ==0; скорости, а соответственно и напряжения сдвига равны нулю:

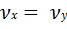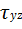= 0; ₌ = 0.

Для решения принимаем допущения, приведенные в предыдущем случае. Уравнения движения в прямоугольных координатах имеют следующий вид.

Проекция на ось x:

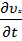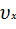
ρ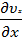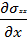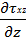( + + ) = - + + + + ρg_x

Проекция на ось y:

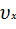
ρ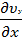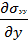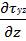( + + ) = - + + + + ρg_y

Проекция на ось z:

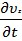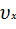
ρ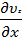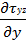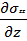( + + ) = - + + + + ρg_z

Проанализировав уравнения движения с учетом принятых условий и допущений, получаем сходное выражение:

=

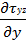Так как = const, после интегрирования имеем:

y + C₁ (6.10)

Используя граничные условия y=0, 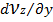=0 (градиент скорости в центре канала равен нулю), имеем = 0, тогда С₁ = 0. С учетом полученных значений, имеем:

y

Напряжение сдвига на стенке при y = H/2 и перепаде давления в канале ∆p = p₀ – p равно:

= -

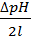
Реологическое степенное уравнение для движения между пластинами с учетом (5.2), (5.5) и (5.7) имеет вид:

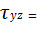K( )ⁿ

Подставив вместо его значение из (6.10), находим:

= ( )^1/ny^1/n

Проинтегрировав это выражение, получаем:

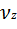= ( )^1/n y^(1+n)/n+C₂

Постоянная интегрирования находится при y = H/2, 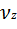=0, тогда:

C₂ = - ( )^1/n ( )^(1+n)/n

Подставив вместо С₂ его значение, находим:

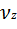= [1-( 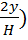^(1+n)/n] (6.11)

где = - 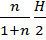( )^1/n

Для вывода уравнения расхода расплава выделим в сечении элемент толщиной dy и шириной B.

Проинтегрировав произведение скорости 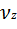на площадь сечения Bdy в пределах от 0 до H/2, находим объемный расход расплава:

V = BH (6.12)

Уравнение скорости сдвига получаем, продифференцировав (6.11) и использовав (6.12):

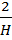= ± ( )^(1+n)/ny^1/n

Скорость сдвига на поверхности пластины при y = H/2 равна:

Дата добавления: 2014-01-05