Ортогональные матрицы

Действия над линейными операторами.

Диагональный вид матрицы линейного оператора

Пусть имеем линейный оператор с матрицей А.

Теорема: «Условие диагональности матрицы»

Матрица линейного оператора имеет диагональный вид тогда и только тогда, когда каждый базисный вектор является собственным вектором этого оператора Z

Приводимой к диагональному виду называется такая матрица А, у которой существует невыраженная матрица, для которой: Т^-1·A·I, полученная матрица называется диагональной. Чтобы построить матрицу I нужно определить собственные числа из характеристического уравнения для матрицы А.

Теорема: Матрица А линейного оператора IR^N-го пространства приводится к диагональному виду тогда и только тогда. Когда существует базис этого пространства, состоящий из собственных векторов. Доказательство основывается на предыдущей теореме и определении.

Матрица будет приводится к диагональному виду, если все её собственные числа λ_i попарно различные.

Произведением (композицией) линейного оператора А на линейный оператор В называется линейный оператор являющийся последним применением операторов А и В, обозначается: В×А, т.е. для вектора Х имеет вид: В×Ах=В(Ах)

Произведение линейных операторов, само является оператором.

Действительно для любых х и у исходя из определения линейного оператора получим:

В×А=(λх+βу)=В(А(λх+βу))=В(А(λх)+А(βу))=λВ(Ах)+βВ(Ау).

Теорема: если в некотором базисе линейного оператора А и В имеют соответственно матрицы А и В, то их произведение В×А имеет матрицу В·А

Сумма многих операторов А и В некоторого линейного пространства, имеет такой оператор К, что для любого вектора х выполнится равенство:

Кх=Ах+Вх

Для оператора справедлива формула: А+В=В+А

Теорема: если линейные операторы А и В в некотором базисе имеют в этом же базисе матрицу (А+В).

Линейные операторы могут быть вырожденными и невырожденными.

Теорема: произведение двух невырожденных операторов, есть невырожденный оператор.

Доказательство:

Пусть матрицы А и В – матрицы невырожденных операторов А и В. тогда det A ≠0, (∆A≠0), det B≠0 (∆B≠0)

Произведению многих операторов соответствует матрица В·А. покажем что она тоже является невырожденной: det(B·A)=detB·detA≠0 => и оператор является невырожденным.

Пусть имеется Евклидово IR^N-ное пространство.

Матрица ортонормированной системы векторов:

а₁=(а_11­, а₂₁,…, а_n1)

а₂=(а_12­, а₂₂,…, а_n2)

а_n=(а_1n­, а_2n,…, а_nn)

называется ортогональной.

Для ортонормированных векторов имеет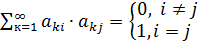

Единичные матрицы ортогональны, пример (det=1)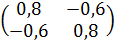

Теорема: для того. Чтобы матрица А была ортогональной, необходимо и достаточно чтобы выполнилось равенство: А^т·А=Е

Доказательство:

Пусть В= А^т·А, то элементы матрици будут равны:

(1)

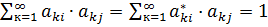
- элементы транспонированной матрицы, поэтому «=» означает, что В=Е=> А^т·А=Е, и обратно если А^т·А=Е, то имеем равенство (1), что означает ортогональность матрицы А.

С1: модуль определителя ортогональной матрицы равен еденице

С2: ортогональная матрица невырожденная

С3: произведение двух ортогональных матриц – ортогональная матрица

С4: необходимым и достаточным условием ортогональности матрицы А является условие: А^т=А^-1

С5: при транспонировании ортогональной получится ортогональная матрица

С6: матрица обратная ортогональной тоже ортогональна, но в сумме ортогональных матриц не является ортогональной.

Матрица перехода от одного ортонормированного базиса к другому является ортогональной.

Ортогональный оператор – это оператор Евклидова пространства, матрица которого ортогональна, в некотором ортонормированном базисе.

Теорема: линейный оператор Евклидова пространства является ортогональным тогда и только тогда, когда она переводит ортонормированный в ортонормированный.

Известно что ортогональный оператор не меняет скалярного произведения вектора(=> из выражения скалярного произведения через координаты векторов в ортонормированном базисе, а => не меняется норма вектора и угол)

Любой ортогональный оператор является не вырожденным.

Симметричные операторы Евклидова пространства:

Линейный оператор А Евклидова пространства Е_n называется симметрическим или самосопряжённым, если для любых 2ух векторов а и b этого пространства выполняется равенство: (Аа, b)=(a, Ab), т.е. если в скалярном произведении символ оператора может переносить с одного множества на другой.

Симметричный оператор Евклидова пространства, в любом ортонормированном базисе, задаётся симметрической матрицей(условие верно и наоборот).

Доказательство:

Пусть вначале симметричный оператор А в ортонормированном базисе е^­₁, е^­₂,…, е^­_n задаётся матрицей 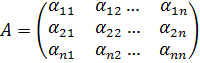т.е. справедливо равенство: Ае=А·е, так как базис ортонормированный то из аксиом скалярного произведения получим:

(Ае_i, e­_j)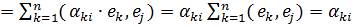

(e­_j, Ае_i)=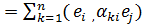

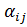
Поскольку А симметричный оператор, то из определения симметрического оператора: А=>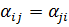

A – линейный оператор заданный в базисе е₁, е₂,… е_n, 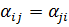- справедливо для всех элементов матрицы А. возьмем произвольно 2 вектора пространства:

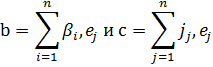
(Ab, c)=(b, Ac),

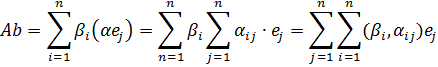
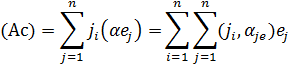
Поскольку, е₁ … е_n – ортогональный базис

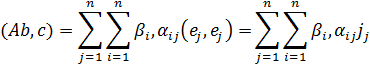
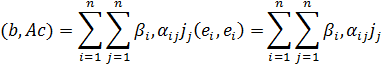
а так как α_ij= α_ji, то (Ab,c)=(b,Ac)

Теорема: ­ все характеристические корни симметричного оператора действительны.

Теорема: линейный оператор Евклидова пространства тогда и только тогда может быть симметрическим, когда в пространстве найдётся ортонормированный базис, каждый вектор которого, является собственным вектором оператора.

Собственные векторы симметричного оператора, относится к различным собственным, значения ортонормированны между собой.

Т₂: Квадратичные формы

f(x₁,x₂,…,x_n)=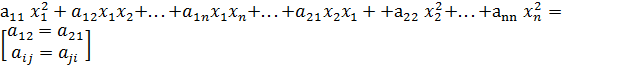

Пример: пусть дана квадратичная форма:

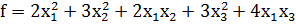
A=

Приведение квадратичной формы к нормальному виду.

Квадратичная форма f(x₁,x₂,…,x_n) называется канонической, если она не содержит произведений различных переменных, т.е.

f(x₁,x₂,…,x_n)=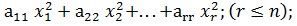

r – ранг квадратичной формы

Каноническая квадратная форма называется нормальной, если: (a_ii)=1, т.е. отличные от нуля, коэффициенты при квадратных переменных =1 или=-1

f=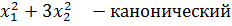

f=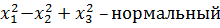

Если квадратичная форма f с матрицей А ранга r, невырожденным линейным преобразованием, приводится к каноническому виду, то количество отличных от нуля коэффициентов b=r.

Матрица канонического вида имеет диагональный вид.

Теорема: любая квадратичная форма некоторых невырожденным линейным преобразованиям, может быть преобразована к каноническому типу.

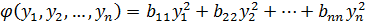
Где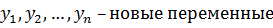

Доказательство:

Докажем методом матричной индукции.

При n=1 теорема верна: f(x₁)=, докажем теорему для квадратичных форм от n-ых переменных. Предположим что среди коэффициентов a_ii квадратичной формы f(x₁,x₂,…,x_n)=, имеется а₁₁≠0, тогда:

;

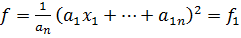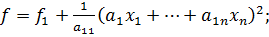
Перейдя к новым переменным у:

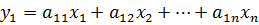
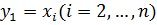; получим квадратичную форму f₂=f₂(y₂,…,y_n), так как квадратичная форма зависит от количества переменных, по предположению и можно привести к каноническому виду => квадратичная форма 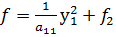, может быть приведена к каноническому виду.

Преобразование переменных являющиеся невырожденными

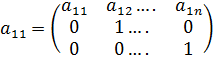; a₁₁≠0 (*)

ð Невырожденная «а» и приводит к виду *

Если известен ранг формы, то задание любого из трёх указанных чисел.

Теорема: две действительные квадратичные формы от n-переменных когерентны тогда и только тогда, когда они имеют одинаковые ранги и сигнатуры

Действительная квантовая форма является f-неположительной опорной, если они приводятся к нормальному виду, состоящего из n-положительных.

Теорема: квадратичная форма f с действительной матрицей является тогда и только тогда, когда её миноры положительны. Т.е. миноры порядка 1 и 2 и т.д. матрицы А, расположены в левом верхнем ряду.

Теорема: если существует ортогональное преобразование с матрицей С приводящая действительную квадратичную форму: f(x₁,…,x_n) к каноническому виду φ(у₁,…,у_n)=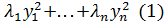, то 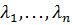n-характеристические числа матрицы А, квадрат формы f.

Доказательство:

Пусть ортогонально преобразован Х=СУ, где С приводит квадратичную форму f к каноническому виду (1), тогда матрица формы φ имеет вид: ; поскольку D=C^TA∙C, см теорему выше, и С ортогональная матрица то С^Т=С^-1 => D= С^-1∙A∙C => λ_i – являются характеристическими числами матрицы А, принимая во внимание выражение D=C^TA∙C, С^-1∙С=Е и умножая слева на матрицу С первое равенство, получаем: CD=CC^T∙A∙C; CD=CC^-1∙A∙C; CD=AC =>

=> AC=C (2)

Для элементов b_ij матрицы В, В=АС, согласно правилу умножения выполнится равенство: b_ij= а_i1 ∙с_1j + а_i2 ∙с_2j +…+а_in ∙с_nj

С другой стороны из (2) получаем что b_ij= с_ij ∙λ_j => выполнится равенство: а_i1 ∙с_1j + а_i2 ∙с_2j +…+а_in ∙с_nj= с_ij ∙λ_j

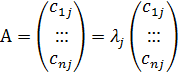
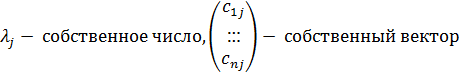
Итак j-столбец матрицы С является собственным вектором столбцом матрицы А с собственным числом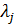

Теорема: для любой действительной квадратичной формы существуют ортогональные преобразования приводящие её к каноническому виду.

Теорема: для любой действительной симметричной матрицы А существует такая ортогональная матрица Т, что Т^-1∙А∙Т – является диагональной матрицей.

Доказательство:

А – действительная симметричная матрица порядка n.

f(x₁,…,x_n) – квадратичная форма матрицы А, тогда по предыдущей теореме существует ортогональное преобразование приводящее форму к каноническому виду. Тогда обозначив матрицу этого преобразования как Т, получаем Т^Т∙А∙Т=D, где D – дополнительная матрица. Так как матрица Т-матрица ортогонального преобразования, то Т^-1= Т^Т и подставив в предыдущее получаем: Т^-1∙А∙Т=D.

С: Любая действительная симметричная матрица может быть приведена к диагональному виду.

Теорема: если линейное преобразование линейного пространства имеет действительную симметричную матрицу, в некотором ортогональном базисе, то существует ортогональный базис, состоящий из собственных векторов этого преобразования.

Из этих теорем следует правило ортогонального преобразования, приводящее квадратичную форму к каноническому виду:

1. Записать матрицу данной квадратичной формы. Найти найти её собственное значение и n-парно-ортогональных собственных векторов. Пронормировать их.

2. Составить матрицу из ортонормированных собственных векторов столбцов.

3. Записать искомое ортогональное преобразование с помощью исходных матриц

Пример:

Найти ортогональное преобразование приводящее к каноническому виду, квадратичную форму.

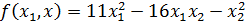
1) a₁₁=11, a₁₂= a₂₁=-16/2=8, a₂₂=-1

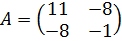
2) чтобы найти собственное значение |A-λE|=0

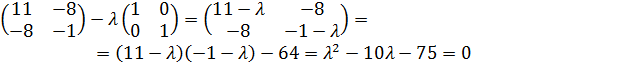
D=400

λ₁=-5; λ₂=15

3) (для каждого собственного значения найти собственный вектор)

λ₁=-5

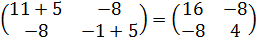
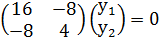
-8у₁+4у₂=0

4у₂=2у₁, (у₁; 2у₁), у₁=С => собственный вектор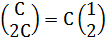

=>собственный вектор у=

λ₂=15

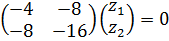
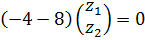
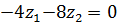
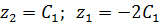
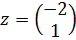
4) Нормируем:

|z|=

5) См 2п.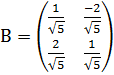

6) См 3п. Х=ВУ

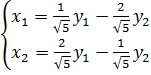
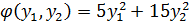
Существует 2 метода:

1. Метод Якоби (приведение квадратичной формы к каноническому виду)

Применяют, когда все главные миноры квадратичной формы отличны от 0.

Тогда справедлива формула:

f(x₁,x₂,…,x_n)=Х^Т∙А∙Х=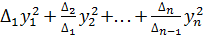

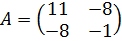
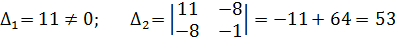
2. Метод Лагранжа (приведения квадратичной формы к каноническому виду).

Основная идея метода заключается в последнем дополнении квадратичного 3х члена по каждому аргументу до полного квадрата.

Дата добавления: 2014-01-05