Рівняння нерозривності рідини

Умова руху рідини без утворення розривів (порожнин) характеризується рівнянням нерозривності потоку рідини, яке виражає закон збереження маси.

Рівняння нерозривності рідини може бути виражене в диференціальній формі (для точки у потоці рідини), для елементарної струминки і для потоку рідини. В інженерній практиці широко використовується рівняння нерозривності для потоку рідини, яке випливає з рівняння нерозривності для елементарної струминки.

У випадку усталеного руху рівняння нерозривності струминки можна отримати, виходячи з властивостей елементарної струминки. Згідно з ними рідина із струминки не витікає на сторону і не притікає із зовнішнього середовища в цю струминку, але в той же час місцеві швидкості різні по довжині струминки. З цього виходить, що кількість рідини, яке тече у струминці у початковому і кінцевому перетинах є однаковою. Незмінним залишається також і об’єм рідини в струминці.

Виділимо у потоці елементарну струминку (рис. 4.4) і розглянемо її відрізок між перерізами 1-1 та 2-2. За час dt у простір між перетинами 1-1 та 2-2 ввійде кількість рідини, яка дорівнює шляху, що проходять частинки рідини між цими перетинами за час dt. Цей шлях дорівнює u₁ dt і тому об’єм циліндра потоку рідини дорівнює u₁ dt dω₁. Відповідно через перетин 2-2 витікає об’єм рідини, який дорівнює u₂ dt dω₂.

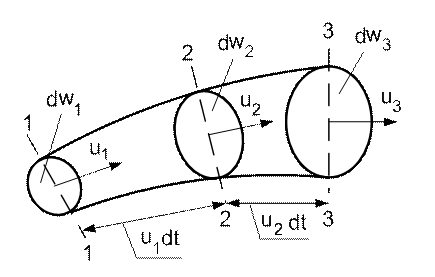
Рис. 4.4

Взявши до уваги, що маса рідини в елементарній струминці залишається постійною, можна записати

ρ₁ u₁ dt dω₁ = ρ₂ u₂ dt dω₂ (4.7)

Після скорочення на dt для нестисливої рідини (ρ = const) отримаємо

u₁ dω₁ = u₂ dω₂ (4.8)

Перетини 1-1 та 2-2 вздовж струминки вибрані довільно, тому аналогічно й для інших перетинів можна записати

u₁ dω₁ = u₂ dω₂ = …= u_n dω_n = const (4.9)

Рівняння (4.8) є рівнянням нерозривності для елементарної струминки нестисливої рідини. З рівняння (4.7) – (4.9) випливає, що при усталеному русі елементарної струминки стисливої рідини залишається постійною масова витрата рідини, а для нестисливої рідини – об’ємна витрата.

Якщо між двома перетинами потоку немає витікання або притоку рідини, то рівняння нерозривності визначиться з умови постійності масової витрати для ρ ≠ const або постійності об’ємної витрати при ρ = const. Оскільки потік складається із безлічі елементарних струминок, то по всій площі двох перетинів нестисливої рідини можна провести інтегрування

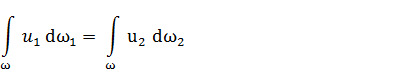
Кожен інтеграл можна записати у вигляді, аналогічному (4.4)

де v₁ та v₂ – середні швидкості для двох перетинів потоку.

Тоді для будь-яких інших перетинів потоку можна записати

v₁ ω₁ = v₂ ω₂ = … =v_n ω_n = Q =const (4.10)

Рівняння (4.10) є рівнянням нерозривності для потоку або рівнянням сталості витрати. Це рівняння показує, що під час руху потоку в різних його перетинах можуть змінюватися середня швидкість v та площа перетину ω, але витрата вздовж потоку залишається незмінною.

Із рівняння (4.10) видно, що середні швидкості потоку обернено пропорційні площам відповідних живих перетинів

v₁ /v₂ = ω₂/ω₁ (4.11)

У загальному випадку для потоку стисливої рідини рівняння нерозривності матиме вигляд

ρ₁ v₁ ω₁ = ρ₂ v₂ ω₂ = … = ρ_n v_n ω_n = M =const (4.12)

Дата добавления: 2014-01-05