Особенности машинной арифметики

Для представления вещественных чисел в компьютере применяют, в основном, два способа: с фиксированной и с плавающей запятой (точкой).

Пусть в основу запоминающего устройства машины положены однотипные физические устройства (базисные элементы), имеющие r устойчивых состояний (как правило, r = 2, 8, 16 и т.п.), причем каждому числу ставится в соответствие одинаковое количество k этих элементов и, кроме того, с помощью таких или более простых элементов может фиксироваться знак. Упорядоченные элементы образуют разрядную сетку машинного слова: в каждом разряде может быть записано одно из базисных чисел 0, 1,..., r – 1 (одна из r «цифр» r-ичной системы счисления) и в специальном разряде отображен знак + или –.

При записи числа с фиксированной запятой кроме упомянутых r параметров (основания системы счисления) и k (количества разрядов, отводимых под запись цифр числа) указывается еще количество l разрядов, выделяемых под дробную часть числа. Таким образом, положительное вещественное число а, представляющее собой в r-ичной системе бесконечную, вообще говоря, непериодическую дробь, здесь будет отображено конечной последовательностью

a₁a₂…a_k–la_k–l+1…a_k–1a_k, где a_i Î {0, 1, …, r – 1}, т.е. реализуется приближенное равенство

a» fix(a) = a₁r^k–l–1 + a₂r^k–l–2 +…+ a_k–1r⁰ + a_k–1+1r^–1 +…+ a_k–1r^–(l–1) + a_kr^–l.

Диапазон представляемых таким способом чисел определяется числами с наибольшими цифрами во всех разрядах, т.е. наименьшим –(r – l)(r – l)…(r – l) и наибольшим (r – l)(r – l)…(r – l) числами, а абсолютная точность представления есть оценка величины |a – fix(a)|, зависящая от способа округления: это r^–l при простом отбрасывании «хвоста» a_k+1r^–(l+1) + a_k+2r^–(l+2) + … числа а и половина этой величины при правильном округлении (т.е. при увеличении a_k на единицу, если ). Заметим, что абсолютная точность представления вещественных чисел с фиксированной запятой одинакова в любой части диапазона. В то же время относительная точность, т.е. оценка величины (или ), очевидно, может значительно различаться в зависимости от того, берется a близким к нулю или к границе диапазона. Иными словами, вещественные числа с фиксированной запятой имеют равномерную абсолютную плотность распределения на всем отрезке вещественной оси, определяемом границами диапазона, и неравномерную, возрастающую к границам отрезка, относительную плотность распределения.

В основе значительно чаще употребляемого представления с плавающей запятой лежит следующая экспоненциальная форма записи вещественного числа:

а = Μ · r^p,

где r основание, p порядок, а М такое, что r^–1 £ |М| < 1 (= r⁰) — мантисса. Если под мантиссу выделяется l r-ичных элементов, а под порядок m, то в системе записи с плавающей запятой вещественное число a представляется конечным числом fl(a) (от англ. floating — «плавающий») вида

a» fl(a) = ±(b₁r^–1 + b₂r^–2 + … + b_lr^–l) · r^g,

где γ целое число из промежутка [–r^m, r^m – 1]; b₁ Î {1, …, r – 1}; β_i Î {0, 1,..., r – l}, (i = 2,..., l), т.е. машинное слово условно имеет структуру:

Числа 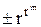определяют границы допустимого числового диапазона. Более информативно здесь нужно говорить о диапазоне представимости положительных вещественных чисел, составляющем промежуток 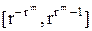. Левую и правую границы этого отрезка называют соответственно машинным нулем и машинной бесконечностью, так как числа из промежутка 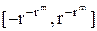машина заменяет нулем, а числа, лежащие за пределами промежутка , она не воспринимает (без специальных ухищрений).

Определение 5. Машинный эпсилон.

Важной характеристикой является число ε, называемое машинный эпсилон и обозначаемое обычно идентификатором macheps. Эта характеристика определяется как расстояние между единицей и ближайшим следующим за ней числом системы машинных чисел с плавающей запятой. Так как

1 = (1·r^–1 + 0·r^–2 +... + 0·r^–l +...}·r¹,

а следующее за 1 машинное число есть

(l·r^–1 + 0·r^–2 +... + 0·r^–(l–1) +l·r^–l)·r¹ =fl(1 + e),

то за macheps можно принять величину

e = 1·r^–l·r¹ = r^l–1.

Это число непосредственно связано с относительной погрешностью представления чисел в системе с плавающей запятой. Имеем:

. (5)

Таким образом, машинный эпсилон служит мерой относительной точности представления вещественных чисел, причем эта точность одинакова в любой части числового диапазона и зависит лишь от числа r-ичных разрядов, отводимых под мантиссу числа. В то же время оценка абсолютной погрешности

|a – fl(a)| £ |fl(a)|·r^1–l

показывает, что расстояние между вещественными числами и конечными приближениями к ним в системе с плавающей запятой неодинаковы в разных частях числового диапазона: абсолютная плотность машинных чисел больше вблизи нуля при одинаковой относительной плотности их распределения.

Приведем значения введенных выше теоретических параметров для некоторой ЭВМ.

Так, для записи числа в 48-разрядном машинном слове ЭВМ 40 двоичных разрядов выделяются под мантиссу, 6 — под порядок и 2 — под знаки мантиссы (т.е. числа) и порядка. Отсюда, принимая r = 2, l = 40, m = 6, получаем, что точность представления чисел с плавающей запятой на этой ЭВМ не хуже 2^–39 (»10^–12), граница машинного нуля 2^–64 (»10^–19), машинной бесконечности 2⁶³ (»10¹⁹).

Дата добавления: 2014-01-05