
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Иррациональные числа и их свойства
|
|
|
|
Существуют отрезки, длина которых не является рациональным числом. Например, диагональ единичного квадрата  . Если число непредставимо в виде дроби
. Если число непредставимо в виде дроби 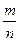 , то оно иррациональное (то есть нерациональное). Будем обозначать множество иррациональных чисел буквой I.
, то оно иррациональное (то есть нерациональное). Будем обозначать множество иррациональных чисел буквой I.
Произвольные числа – рациональные или иррациональные, называются действительными или вещественными. Множество вещественных чисел будем обозначать буквой R.
 ,
, 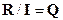 .
.
Существуют различные способы введения действительных чисел. Остановимся на способе представления числа в виде бесконечных десятичных дробей  ,
, 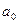 – некоторое целое неотрицательное число,
– некоторое целое неотрицательное число,  ,
, 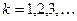 .
.
Дробь  – конечная.
– конечная.
Дробь 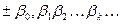 – бесконечная, если
– бесконечная, если 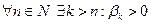 .
.
Разложение рационального числа имеет вид:
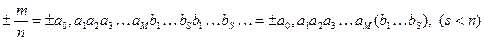 – бесконечная десятичная периодическая дробь.
– бесконечная десятичная периодическая дробь.
J Пример 2.1.  ,
,
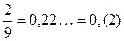 ,
,
 . J
. J
Кроме периодических десятичных дробей, существуют непериодические дроби, например  ,
,  – это иррациональные числа.
– это иррациональные числа.
Таким образом, иррациональное число – это произвольная бесконечная непериодическая дробь.
♦ Предложение 2.1. Любое действительное число можно приблизить с любой степенью точности рациональным числом.
Доказательство. Пусть 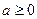 представлено в виде бесконечной десятичной дроби
представлено в виде бесконечной десятичной дроби . Тогда в силу операции упорядочения вещественных чисел справедливо неравенство
. Тогда в силу операции упорядочения вещественных чисел справедливо неравенство 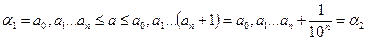 для любого номера n. Ясно, что
для любого номера n. Ясно, что  . Покажем, что для
. Покажем, что для  найдется n такое, что выполняется неравенство
найдется n такое, что выполняется неравенство  . В силу аксиомы Архимеда для
. В силу аксиомы Архимеда для  , то есть найдется лишь конечное число натуральных чисел таких, что
, то есть найдется лишь конечное число натуральных чисел таких, что 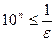 или
или  . ■
. ■
Таким образом, справедлива
♦ Лемма 2.1. Для любого вещественного числа a и для любого наперёд взятого положительного рационального числа ε найдутся два рациональных числа 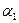 и
и  такие, что
такие, что 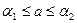 , причём
, причём  .
.
|
|
|
♦ Лемма 2.2. Каковы бы ни были два вещественных числа a и b такие, что a>b, найдётся рациональное число 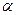 , заключённое между ними, то есть такое, что
, заключённое между ними, то есть такое, что  (а следовательно, найдётся и бесконечное множество различных рациональных чисел, заключённых между a и b).
(а следовательно, найдётся и бесконечное множество различных рациональных чисел, заключённых между a и b).
Доказательство. 1) Пусть 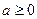 ,
, 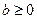 ,
,  ,
,  ,
,  . Пусть
. Пусть  ,
, 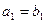 , …,
, …,  ,
, 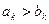 , причём все десятичные знаки
, причём все десятичные знаки 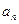 при n > k не могут быть равны нулю (иначе число a будет представлено в виде
при n > k не могут быть равны нулю (иначе число a будет представлено в виде  ). Пусть на некотором месте n = p > k стоит первый ненулевой десятичный знак
). Пусть на некотором месте n = p > k стоит первый ненулевой десятичный знак 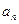 , то есть
, то есть  . Тогда рациональное число
. Тогда рациональное число 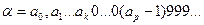 удовлетворяет неравенствам
удовлетворяет неравенствам  .
.
2) Пусть  ,
, 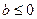 . Рассматривая модули чисел, воспользуемся доказательством пункта 1).
. Рассматривая модули чисел, воспользуемся доказательством пункта 1).
3) Если 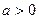 ,
,  , то
, то  . ■
. ■
♦ Лемма 2.3. Пусть 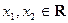 . Если для
. Если для  найдутся
найдутся 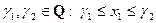 ,
, 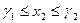 ,
, 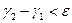 , то
, то 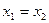 .
.
Доказательство. Предположим, что 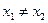 , скажем,
, скажем,  . Тогда в силу леммы 2.2 найдутся рациональные
. Тогда в силу леммы 2.2 найдутся рациональные 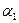 и
и  :
: 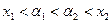 . Пусть
. Пусть 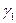 и
и 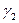 - какие угодно рациональные числа, удовлетворяющие неравенствам
- какие угодно рациональные числа, удовлетворяющие неравенствам  ,
, 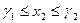 . Тогда
. Тогда 
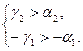 Следовательно,
Следовательно, 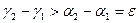 , что противоречит условию
, что противоречит условию  . То есть предположение неверно и
. То есть предположение неверно и 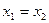 . ■
. ■
2.3. Счётность множеств R и Q.
♦ Теорема 2.1. Множество рациональных чисел Q счётно.
Доказательство. Рассмотрим  . Назовем натуральное число
. Назовем натуральное число  высотой рационального числа
высотой рационального числа 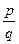 . Пусть An – множество всех рациональных чисел с высотой n. Множества An состоят из конечного числа элементов (рациональных чисел), например:
. Пусть An – множество всех рациональных чисел с высотой n. Множества An состоят из конечного числа элементов (рациональных чисел), например:
 ,
, 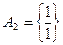 ,
,  ,
, 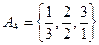 , ….
, ….
Отсюда 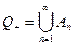 .
.
Перенумеруем числа в 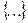 слева направо, опуская те, которые уже пронумеровали. Таким образом, получим последовательность:
слева направо, опуская те, которые уже пронумеровали. Таким образом, получим последовательность: 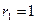 ,
, 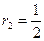 ,
,  ,
,  ,
, 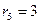 , …. Т.к. рациональных положительных чисел бесконечно много, мы используем все натуральные числа. Значит
, …. Т.к. рациональных положительных чисел бесконечно много, мы используем все натуральные числа. Значит 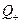 – счётно.
– счётно.
Очевидно, что  – счётно.
– счётно. 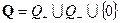 – счётно. ■
– счётно. ■
♦ Теорема 2.2. Множество действительных чисел R несчётно.
Доказательство. Докажем, что множество действительных чисел 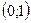 образует несчётное множество. Допустим, что
образует несчётное множество. Допустим, что 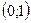 – счётное множество, то есть все точки можно пронумеровать:
– счётное множество, то есть все точки можно пронумеровать:

Это предположение противоречиво. В самом деле, построим вещественное число 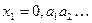 , где цифры
, где цифры  и
и  .
.
|
|
|
Ясно, что 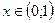 , однако x не совпадает ни с одним из
, однако x не совпадает ни с одним из  , т.к. иначе
, т.к. иначе  , что не имеет места. Таким образом,
, что не имеет места. Таким образом, 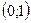 – несчётно, а значит, и множество R тоже несчётно. ■
– несчётно, а значит, и множество R тоже несчётно. ■
|
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 1640; Нарушение авторских прав?; Мы поможем в написании вашей работы!