Интегрируемость систем. Резонансы

Интегрируемые системы. Резонансы. Периодические и квазипериодические движения. Резонансные и нерезонансные торы. Теорема А. Пуанкаре о неинтегрируемости. Результаты теории КАМ

Интегрируемые системы. Основной проблемой в классической динамике является проблема интегрирования. Коль скоро мы располагаем уравнениями движения, нам, естественно, хотелось бы получить явные выражения для переменных (координат, скоростей) как функций времени. А. Пуанкаре показал, что найти такие выражения в общем случае невозможно.

Существуют системы двух типов: интегрируемые и неинтегрируемые. Для интегрируемых систем можно исключить взаимодействия и свести задачу к задаче о свободном движении. Для свободного движения не составляет труда найти выражения для координат и скоростей в виде явных функций времени. Для неинтегрируемых систем необходимо отказаться от описания в терминах траекторий и перейти к вероятностному описанию. Речь идет о принципиально вероятностном описании, несводимом к описанию в терминах отдельных траекторий.

Основная проблема ньютоновской механики –расчет движения взаимодействующих тел на основе уравнения F = ma, связывающего ускорение (то есть вариацию состояния движения) с силой.

С траекторией связаны такие величины, как координаты тела x (t), скорость x ¢(t) = d x (t)/dt и ускорение a = x ¢¢(t) = d² x (t)/dt². Время входит в уравнение Ньютона только через вторую производную. Вследствие этого уравнение Ньютона остается инвариантным при замене t на - t.

Закон Ньютона служит прототипом «закона природы»: он обратим во времени и детерминистичен. Зная начальное положение x ₀ и начальную скорость x ¢₀, можно приступить к интегрированию уравнения Ньютона и найти положение и скорость тела в любой момент времени t до и после t₀.

В общем случае состояние динамической системы задается координатами x₁, x₂,, x_s, являющимися независимыми переменными, и соответствующими им скоростями x¢₁, x¢₂,, x¢_s, являющимися зависимыми переменными, поскольку определяются как производные от координат по времени.

Современная физика использует вместо ньютоновского описания гамильтоновское. В гамильтоновском описании присутствуют координаты q₁, q₂,, q_s и скорости или, точнее, импульсы p₁, p₂,, p_s (в простых ситуациях импульс равен произведению массы на скорость: p_i = m x¢_i), определяются как независимые переменные. Преимущество такого подхода заключается в существенном упрощении уравнений движения.

Центральная величина всей гамильтоновской механики - функция Гамильтона или гамильтониан, H.

Гамильтоновская динамика рассматривает только консервативные обратимые во времени системы, в которых H не зависит явно от времени. Во многих ситуациях гамильтониан имеет вид

H = E_kin(p₁, p₂,, p_s) + V_pot(q₁, q₂,, q_s).

E_kin(p₁, p₂,, p_s) – кинетическая энергия системы, зависящая от импульсов и не зависящая от координат.

V_pot(q₁, q₂,, q_s) – потенциальная энергия системы, зависящая только от координат.

В гамильтоновском описании число независимых переменных удваивается (в ньютоновском уравнении независимыми переменными являются только координаты), но уравнения движения существенно упрощаются.

Рассмотрим систему N точек. Каждой из 3N координат этих точек соответствует каноническое уравнение движения

dq/dt = ¶H/¶p.

Аналогично, каждому из 3N импульсов соответствует каноническое уравнение движения

dp/dt = - ¶H/¶q.

В качестве частного случая рассмотрим свободные, т.е. не взаимодействующие, частицы. Гамильтониан зависит только от импульсов (потенциальной энергии нет). Из канонических уравнений следует, что импульсы постоянны во времени (¶H/¶q = 0) и что координаты, задающие положение частиц – линейные функции времени. Ясно, что это тривиальный случай, но он играет очень важную роль в общей проблеме интегрирования гамильтоновых уравнений движения.

Для динамической системы, состоящей из N частиц, фазовое пространство 6-мерно (3N координат и 3N импульсов) Каждое состояние динамической системы может быть представлено точкой в фазовом пространстве. Начальное состояние вместе с гамильтонианом полностью определяет траекторию. В результате две траектории, исходящие из разных начальных точек, навсегда останутся различными. Они никогда не пересекутся и не сольются в одну общую траекторию. Каждая точка в фазовом пространстве принадлежит одной и только одной траектории.

Чтобы упростить гамильтоновы уравнения, введем новые переменные a и J вместо старых p и q. Новые переменные удовлетворяют каноническим уравнениям движения и связаны с p и q соотношениями

q = Ö 2J/mw ´ Sin a и p = Ö 2Jmw ´ Cos a. Это означает переход к полярным координатам: J – переменная действия, a – угловая переменная.

В результате dJ/dt = - ¶H/¶a = 0, т.е. переменная действия является инвариантом движения.

Что же касается переменной a, то da/dt = - ¶H/¶J = w. Следовательно эволюция угловой переменной во времени описывается линейной функцией

a = w t + a₀.

Переход от переменных p, q к переменным J, a называется каноническим преобразованием. Такое преобразование позволяет исключить взаимодействие (потенциальную энергию) из гамильтониана. В результате движение выражается в терминах циклических переменных J, a, уравнения Гамильтона становятся особенно простыми и легко интегрируются. Действительно, в циклическом представлении гамильтониан H есть функция только переменных действия J₁, J₂,.., J_s. Как и в случае свободного движения, каждый импульс есть инвариант (dJ/dt = 0), и каждое положение, задаваемое угловыми переменными a₁, a₂,..,a_s есть линейная функция времени (da/dt = w).

Возможность исключить потенциальную энергию с помощью преобразования – основная характерная особенность интегрируемых динамических систем в смысле Пуанкаре.

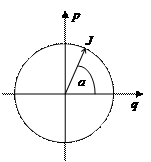Термин циклические переменные для набора переменных, исключающих взаимодействия в гамильтониане, относится к периодическому характеру движения, который делается явным в таких переменных. Если интегрируемая система имеет одну степень свободы, то ее движение можно представить как движение по окружности. В случае двух

переменных мы имеем движение на торе. Очень

важную роль играют частоты системы w₁, w₂,.., w_{s .}

Все они являются производными по времени раз-

личных угловых переменных a₁, a₂,..,a_s и определя-

ются каноническими уравнениями

w_i = da_i/dt = - ¶H/¶J_i.

Именно через эти частоты мы приходим к понятию

резонанса, имеющему решающее значение для теоремы А. Пуанкаре.

Рассмотрим интегрируемую систему с двумя

степенями свободы, движение которой представим

на торе. Возможны две ситуации.

Если k₁w₁ + k₂w₂ = 0, где k₁, k₂ – целые числа, не

равные нулю одновременно, то мы имеем резонанс.

Это означает, что w₁ /w₂ = - k₂ / k₁, то есть отношение

Частот равно рациональному числу. Если есть резонанс, то движение на торе периодическое. Такой тор называется резонансным.

В другом случае, когда сумма k₁w₁ + k₂w₂ отлична от нуля при произвольных целых числах k₁, k₂, изображающая точка никогда не возвращается в начальное положение. В этом случае имеет место квазипериодическое движение - геликоидальная траектория на торе, которая, никогда не замыкаясь, навивается на поверхность тора. Для системы с двумя степенями свободы квазипериодическое движение возникает, например, если w₁ /w₂ = 1/Ö 2.

Квазипериодическое движение выглядит очень сложным, поскольку представляющая траектория нигде не замыкается и не пересекается с собой. Она постепенно заполняет тор. В конце концов такая траектория проходит через любую, сколь угодно малую окрестность произвольной точки на поверхности тора. Такая траектория называется «всюду плотной», а тор - нерезонансным.

Неинтегрируемые системы. Определение интегрируемой системы связано с возможностью исключения взаимодействий между частицами. Как и в случае свободных частиц, гамильтониан после исключения взаимодействий зависит только от импульсов. В терминах переменных угол – действие это означает, что гамильтониан зависит только от переменных действия J и поэтому имеет вид H(J). В этом случае переменные действия являются инвариантами движения (dJ/dt = 0). Именно такие системы А.Пуанкаре назвал интегрируемыми.

А. Пуанкаре показал, что в общем случае невозможно получить каноническое преобразование (сохраняющее вид гамильтоновых уравнений), которое приводило бы к циклическим переменным. Например, система Земля – Солнце в этом смысле интегрируема, но система Земля – Солнце – Юпитер – нет. Подавляющее большинство динамических систем неинтегрируемы.

В терминах теории возмущений гамильтониан может быть задан в виде суммы H₀(J) + lV(J,a). Свободный гамильтониан H₀ соответствует интегрируемой системе, изоморфной системе свободных частиц. Свободный гамильтониан возмущается потенциалом взаимодействия lV(J,a), где l - константа связи (параметр, измеряющий интенсивность взаимодействия).

Задача состояла в том, что бы определить новые переменные действия J = J + lJ₁ + l²J₂ +… (где J₁ и J₂ - функции от J и a) так, чтобы при l®0 новые переменные действия J гладко переходили в J. Иными словами, требовалось найти переменные действия, аналитические по l, то есть функции от J и a, представимые в виде степенных рядов l. Аналитичность замены переменных гарантирует малость отличия J от J при малых l. Если такая замена возможна, то можно исключить потенциальную энергию V(J,a) возмущенной системы и ввести новый гамильтониан, зависящий только от J. Интегрирование возмущенной системы в этом случае было бы столь же простым, так как новые переменные действия J были бы инвариантами движения.

Как показал А. Пуанкаре, теория возмущений неизбежно приводит к появлению членов с опасными знаменателями (для системы с двумя степенями свободы, например, 1/ k₁ w₁ + k₂w ). Если существуют резонансы, то есть такие точки в фазовом пространстве, в которых k₁ w₁ + k₂w = 0, то члены ряда теории возмущений расходятся. Таким членам можно приписать только значение бесконечности. Когда в физике возникают бесконечности, или расходимости, это означает, что что-то не так.

А. Пуанкаре не только доказал неинтегрируемость, но и объяснил причину – существование резонансов между степенями свободы. В отсутствии возмущений резонансы приводят к периодическому движению (резонансные торы). В общем случае имеет место квазипериодическое движение (нерезонансные торы). Периодические движения не правила, а исключения. При введении возмущений характер движения на резонансных торах резко изменится (по теореме А. Пуанкаре), в то время как квазипериодическое движение изменится очень незначительно (при малом возмущении l). А.Н. Колмогоров дал четкое описание тех видов квазипериодического движения, сохраняющих свой тип после наложения возмущения. Для этого связь между собственными частотами должна быть достаточно иррациональной. Для N=2 отношение w₁ /w₂ должно отвечать условию

½w₁ /w₂ - r/s½> c/sⁿ , где r и s – целые, c – малое число, обращающееся в нуль при отсутствии возмущений, n - достаточно большое число (n = 2,5)

Таким образом, мы имеем дело с двумя типами траекторий: слегка изменившиеся квазипериодические траектории и стохастические траектории, возникающие при разрушении резонансных торов (теория КАМ).

Наиболее важный результат теории КАМ – появление стохастических траекторий. Еще один результат этой теории состоит в том, что, увеличивая параметр связи l, мы тем самым увеличиваем области, в которых преобладает стохастичность. При некотором критическом значении l возникает

хаос: в этом случае мы имеем положительный показатель Ляпунова, соответствующий экспоненциальному разбеганию со временем любых двух близких траекторий.

КАМ не приводит к динамической теории хаоса. Ее главный вклад состоит в том, что при малых значениях параметра l мы имеем промежуточный режим, в котором существуют траектории двух типов – регулярные и стохастические.

Дата добавления: 2014-01-05