Лекция 4. Применение теории матриц к решению и исследованию систем линейных уравнений

Применение теории матриц к решению и исследованию систем линейных уравнений

Снова рассмотрим систему трёх линейных уравнений первой степени с тремя неизвестными (см. (1), лекция 2).

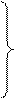а11x1 + a12x2 + a13x3 = b1
а21x1 + a22x2 + a23x3 = b2		(1)
а31x1 + a32x2 + a33x3 = b3

Введём три матрицы:

	а11	а12	а13
А=	а21	а22	а23
	а31	а32	а33

	х1
X =	х2
	х3

	b1
B =	b2
	b3

Используя правило умножения матриц, систему (1) запишем в матричной форме

	а11	а12	а13	х1			b1
B =	а21	а22	а23	х2		=	b2			(2)
	а31	а32	а33	х3			b3

или

AX = B (3)

Это равенство называется простейшим матричным уравнением. Для его решения умножим левую и правую часть слева на матрицу А^-1:

А^-1АX = A^-1B

Так как А^-1A = E, а EX = X, то

X = A^-1B (4)

или в развёрнутом виде

x1			A11	A21	A31	b1
x2	=	1/DA	A12	A22	A32 ^.	b2		(5)
x3			A13	A23	A33	b3

Произведя умножение матриц, находим

x1			b1A11 + b2A21 + b3A31
x2	=	1/DA	b1A12 + b2A22 + b3A32
x3			b1A13 + b2A23 + b3A33

Приравнивая элементы матриц, стоящих слева и справа, получаем

x1 =	b1A11 + b2A21 + b3A31
DA

x2 =	b1A12 + b2A22 + b3A32
DA

x3 =	b1A13 + b2A23 + b3A33
DA

Это решение можно записать в форме определителей:

= = =

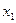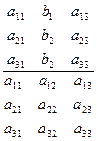
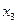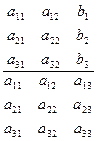
Пример 1. (Маша Куприянова).

Решить систему уравнений:

4x₁ + x₂ – x₄ = -9,

X₁ - 3x₂ + 4x₃ = -7,

3x₂ - 2x₃ + 4x₄ = 12,

x₁ + 2x₂ – x₃ - 3x₄ = 0.

Представим её в виде матричного уравнения и запишем в виде (3), где

						x1		-9
A =		-3			, X =	x2	, B =	-7
		-2		x3
			-1	-3		x4

Решение матричного уравнения имеет вид (4). Найдём А^-1.

Имеем:

								-8
DA =		-3			=			-5	-3	=
		-2				-2
			-1					-1	-3

= - 17 ^. (-26) + 4 ^. 29 – 11 ^. 5 = 121

Вычислим алгебраические дополнения элементов этого определителя:

								-1					-1
A11 =		-2		=38,	A21 = -		-2		=-9,	A31 =	-3			=-7,
		-1	-3				-1	-3				-1	-3
			-1										-1
A41 = -	-3			=-22,	A12 = -		-2		=-26,	A22 =		-2		=38,
		-2					-1	-3				-1	-3
			-1					-1				-3
A32 = -				=43,	A42 =				=66,	A13 =				=-29,
		-1	-3				-2						-3
			-1					-1					-1
A23 = -				=61,	A33 =		-3		=34,	A43 =-		-3		=55,
			-3					-3
		-3
A14 = -			-2	=5,	A24 =			-2	=2,	A34 =-		-3		=15,
			-1					-1					-1
					A44 =		-3		=-22.
								-2

		-9	-7	-22
A^~ =	-26
-29
				-22

следовательно,

		-9	-7	-22	-9
X = 1/121	-26				-7	=
-29
				-22

	38(-9) + (-9)(-7) + (-7)12 + (-12)0		-363		-3
= 1/121	(-26)(-9) + 38(-7) + 43 ^. 12 + 66 ^. 0	=1/121		=
	(-29)(-9) + 61(-7) + 34 ^. 12 + 55 ^. 0
	5(-9) + 2(-7) + 15 ^. 12 + (-22)0

x1			-3
x2		=
x3
x4

Приравнивая строки матриц, стоящих слева и справа, получаем:

x₁ = -3, x₂ = 4, x₃ = 2, x₄ = 1.

Для решения матричного уравнения вида

XA = B (6)

умножим его, в отличии от (3), справа на матрицу А^-1:

XAA^-1 = BA^-1

Учитывая, что АА^-1 = Е, ХЕ = Х, находим

Х = ВА^-1 (7)

Пример 2. (Полина Зубко, КШ-062).

Решить уравнение

	-1					-1
X ^.	-3			=
					-1

Ход мысли Полины:

	-1				-1				-4
1. D =	-3			=	-3	-4		= -			= 16

2.

A11 =			=4,	A21 =-			=-6,	A31 =			=2,
A12 =-	-3		=10,	A22 =	-1		=-3,	A32 =-	-1		=1,
									-3
A13 =	-3		=-8,	A23 =-	-1		=4,	A33 =	-1		=4
									-3

			-6
A^-1 =	1/16 ^.		-3
		-8

		-1				-6
X =				1/16 ^.		-3		=
	-1				-8

	20-10-24	-30+3+12	10-1+12
=1/16 ^.	16+20-8	-24-6+4	8+2+4 =
	-4+0-16	6-0+8	-2+0+8

	-14	-15
=1/16 ^.		-26	14
	-20

Понятие о ранге матрицы

Минором данной матрицы А называется определитель, составленный из оставшихся элементов матрицы после вычёркивания из неё нескольких строк и столбцов.

Рассмотрим, например, матрицу

а11	а12	а13	а14
а21	а22	а23	а24
а31	а32	а33	а34

Миноры третьего порядка этой матрицы получаются после вычёркивания одного столбца и замены знака матрицы () знаком определителя | |. Их четыре. Миноры второго порядка получаются после вычёркивания двух столбцов и одной строки, их 18. Миноров первого порядка 12.

Рангом матрицы А (r_A) называется наивысший порядок отличного от нуля минора этой матрицы.

Можно определение ранга сформулировать и так:

рангом матрицы А (r_A) называется наибольшее натуральное число, для которого существует не равный нулю определитель k – го порядка, порождаемый матрицей А.

Убедитесь, что, например, ранг матрицы

равен 1 (r = 1), а матрицы

	-1

равен 2 (r = 2).

Рассмотрим основные методы вычисления ранга матрицы.

Метод окаймляющих миноров. Пусть в матрице найден минор k – го порядка M, отличный от нуля. Рассмотрим те миноры (k + 1) – го порядка, которые содержат в себе (окаймляют) минор М: если все они равны нулю, то ранг матрицы равен k. В противном случае среди окаймляющих миноров найдётся ненулевой минор (k + 1) – го порядка и обсуждаемую процедуру придётся повторить.

Пример 3. (Маша Куприянова).

Найти ранг матрицы

Фиксируем минор второго порядка, отличный от нуля:

M2 =			≠ 0

Минор третьего порядка

M3 =				,

окаймляющий минор М₃, также отличен от нуля:

M3 =				-2			+11			=

= -3 + 20 - 22 = -5

Однако минор 4-го порядка

M4 =

равен нулю (убедимся сами, повторив ход мысли Маши):

M4 =					= -				=

=	- 11			-10			+42			=

= - (110+110-210) = 0

Следовательно, ранг А равен трём (r_A = 3).

Если r_A = r_B, то матрицы А и В называются эквивалентными. Пишут А~В.

Элементарными преобразованиями матрицы называются следующие:

1. Замена строк столбцами, а столбцов – соответствующими строками;

2. Перестановка строк матрицы;

3. Вычёркивание строки, все элементы которой равны нулю;

4. Умножение какой-либо строки на число, отличное от нуля;

5. Прибавление к элемента модной строки соответствующих элементов другой строки.

Метод элементарных преобразований основан на том факте, что они не меняют ранга матрицы. Используя эти преобразования, матрицу можно привести к такому виду, когда все её элементы, кроме а₁₁, а₂₂,... а_rr (r <= min (m, n)), равны нулю. Следовательно ранг матрицы равен r.

Пример 4. Найти ранг матрицы

A =
				-3
	-1

Слово опять ей, Лене Гладковой!

						-1
A =					~
				-3
	-1								-3

Далее проводим следующие преобразования.

1. а. Элементы первой строки прибавим к соответствующим элементам второй строки;

b. Удвоенные элементы первой строки прибавим к соответствующим элементам третьей и четвёртой строк:

	-1
A =

2. а. Из элементов четвёртой строки вычтем соответствующие элементы второй строки;

b. Из элементов третьей строки вычтем соответствующие элементы второй строки, умноженные на -2:

	-1
A =

3. Из элементо четвёртой строки вычтем соответствующие элементы третьей строки:

	-1
A =

4. Вычёркиваем четвёртую строку, так как все её элементы равны нулю:

	-1
A =

5. Из элементов первого столбца вычтем соответствующие элементы второго столбца:

	-1
A =

6. Умножим элементы первой строки на -1 и прибавим к ней соответствующие элементы третьей строки:

	-1
A =

7. Из элементов четвёртого столбца вычтем удвоенные элементы второго столбца:

		-2
A =				-5

8. К элементам второго столбца прибавим удвоенные элементы первого столбца:

A =				-5

9. К элементам второго столбца прибавим соответствующие элементы четвертого столбца:

A =				-5

10. а. Вычёркиваем второй столбец, так как все его элементы равны нулю;

b. Делим элементы четвёртого столбца на -5:

A =

11. Из элементов второй строки вычтем соответствующие элементы третьей строки:

A =

12. Переставляя строки матрицы А, получаем единичную матрицу.

E =

Ранг этой матрицы определяется числом единиц на её главной диагонали и равен 3. Следовательно, таков же и ранг исходной матрицы: r_A = 3.

Понятие ранга матрицы широко используется в теории систем линейных уравнений.

Запишем ещё раз систему линейных уравнений, с которой я начинал изложение этой лекции.

а11x1 + a12x2 + a13x3 = b1
а21x1 + a22x2 + a23x3 = b2			(1)
а31x1 + a32x2 + a33x3 = b3

Наряду с матрицей системы

	а11	а12	а13
A =	а21	а22	а23
	а31	а32	а33

Введём её расширенную матрицу

	а11	а12	а13	b1
B =	а21	а22	а23	b2
	а31	а32	а33	b3

Вспомним, что система называется совместной, если у неё существует, по крайней мере, одно решение, в противном случае она называется несовместной.

Теорема Кронекера - Капелли. Для совместности системы (1) необходимо и достаточно, чтобы ранг матрицы этой системы равнялся рангу её расширенной матрицы: r_A = r_B. Если ранг матрицы А системы меньше ранга расширенной матрицы В, т.е. r_A < r_B, то данная система несовместна и решения не существует.

Предоставим, читатель, ещё раз слово Маше Куприяновой. Именно ей Вы обязаны знакомством с конспектом этих лекций, именно она совместно с Леной Гладковой взяла на себя нелёгкий труд, напечатав рукопись и отредактировав её. Повторите ход мыслей Маши при решении вопроса, является ли совместной система уравнений (пример 5)

6x₁ + 4x₂ + 5x₃ + 2x₄ + 3x₅ = 1

3x₁ + 2x₂ + 4x₃ + x₄ + 2x₅ = 3

3x₁ + 2x₂ – 2x₃ + x₄ = 7

9x₁ + 6x₂ + x₃ + 3x₄ + 2x₅ = 2

Маша выбрала комплексный подход к определению рангов матрицы А и расширенной матрицы В.

А =						~						~
			-2						-2

~						~					rA=3
			-2						-2

Выписывая расширенную матрицу, отделим элементы матрицы системы (матрицы А) от свободных членов системы.

В =							~							~
			-2			-7				-2			-7

~							~						~
			-2			-7				-2		-7

~						~						~
			-2		-7				-2		-7

~					rB = 3
		-2

Так как r_A = r_B, то система совместна.

Эту лекцию, как и вторую, закончим обсуждением решения системы линейных уравнений методом Гаусса. Практически удобнее подводить к ступенчатому виду не саму систему уравнений, а матрицу из коэффициентов при неизвестных и свободных членов.

Метод Гаусса особенно «пришёлся по душе» Маше Ларькиной (ТШ-062). Ей слово.

Решаем систему уравнений (Пример 6).

3x₁ + 2x₂ + 5x₃ – x₄ = 3

2x₁ - 3x₂ – 3x₃ + 4x₄ = 1

4x₁ + x₂ + 3x₃ + 2x₄ = 3

5x₁ – 2x₂ + x₃ + 3x₄ = 5

1) Выпишем матрицу:

			-1
	-3	-3
	-2

2) Умножим элементы первой строки на 4, 2, 3 и прибавим соответственно к элементам второй, третьей и четвёртой строки. Получим:

			-1

3) Вычтем вторую строку из четвёртой:

3			-1
				-1

4) Умножим элементы второй строки на 10 и вычтем из соответствующих элементов третьей строки, умноженных на 14:

3
				-4
				-1

5) Умножим элементы четвёртой строки на 12 и вычтем из соответствующих элементов третьей строки:

			-1
				-1

6) Используя полученную матрицу, выписываем преобразованную систему, поменяв местами третью и четвёртую строки:

-x₄ + 3x₁ + 5x₃ + 2x₂ = 3

4x₁ + 17x₃ + 5x₂ = 13

x₃ + x₂ = -2

8x₂ = 8

Последовательно находим неизвестные: x₂=1, x₃=-2, x₁=3, x₄=-2.

Приложение

Попытаемся самостоятельно ещё раз проанализировать ход мыслей «суперзвезды» Лены Гладковой, отвечающей на вопрос, является ли система уравнений

8x₁ + 6x₂ + 5x₃ + 2x₄ = 21

3x₁ + 3x₂ + 2x₃ + x₄ = 10

4x₁ + 2x₂ + 3x₃ + x₄ = 8

3x₁ + 5x₂ + x₃ + x₄ = 15

7x₁ + 4x₂ + 5x₃ + 2x₄ = 18

совместной (Пример 7)

						0		-1			0		-1
							-2
A=

Дата добавления: 2014-01-05