Линейная зависимость и независимость векторов

Система векторов называется линейно-зависимой, если хотя бы один из этих векторов является линейной комбинацией остальных, т.е. некоторый вектор можно представить в виде:

,

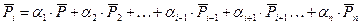где - числовые множители.

В противоположном случае система векторов называется линейно-независимой.

Существует и другое определение линейной зависимости системы векторов.

Система векторов 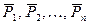называется линейно-зависимой, если существует такие числа 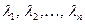по крайней мере одно из которых отлично от нуля, что имеет место равенство:

.

Если же это равенство имеет место тогда и только тогда, когда 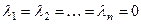, то система векторов линейно-независима.

В n -мерном пространстве существует не более n линейно-независимых векторов. Любая система векторов, состоящая из числа векторов, больше n, является линейно-зависимой в этом пространстве.

Пример 4.6. Определить, является ли система векторов ; ; ; 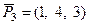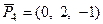линейно-зависимой. Если является, то один из векторов выразить как линейную комбинацию других.

Решение. Имеем четыре вектора в трехмерном пространстве. Следовательно, данная система векторов является линейно-зависимой. Можно решить эту задачу, воспользовавшись вторым определением линейной зависимости системы векторов.

Запишем уравнение:

.

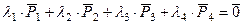Определим значения 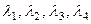. Для этого в равенство подставим данные вектора и произведем соответствующие действия:

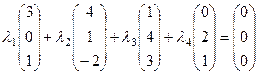
Умножим каждый вектор на и сложим полученные векторы.

Учитывая, что два вектора равны в том случае, если равны их соответствующие координаты, получим однородную систему линейных уравнений:

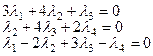
Решаем данную систему методом Жордана-Гаусса:

.

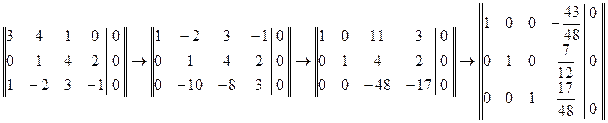На первом шаге принимаем «1» в третьей строке за направляющий элемент, меняем местами данную строку с первой и получаем нули в первом столбце. На втором шаге принимаем за направляющий элемент «1», стоящий во второй строке и во втором столбце. С помощью этой строки получаем нули во втором столбце. На третьем шаге принимаем «-48» за направляющий элемент и делим третью строку на «-48». С помощью полученной строки получаем нули в третьем столбце. Последняя матрица соответствует системе уравнений:

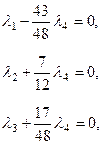
откуда получаем:

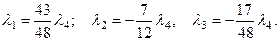
Найденные значения 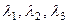подставим в исходное равенство:

Полагая 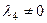, разделим полученное равенство на 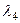. В результате будем иметь следующую зависимость между векторами:

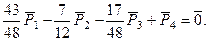
Заметим, что из полученного равенства любой из векторов можно представить, как линейную комбинацию остальных векторов, например:

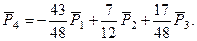
Пример 4.7. Доказать, что векторы , и компланарны.

Решение.

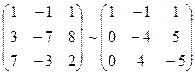, т.к. векторы линейно зависимы, то они компланарны.

Пример 4.8. Являются ли векторы 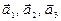линейно зависимыми?

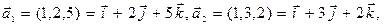
Решение. Составим линейную комбинацию и приравняем ее нулю , где 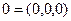– нуль вектор.

Если все 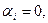то система линейно независимая. Используя правила умножения вектора на число, сложение и сравнение векторов, заданных своими координатами, получим следующую систему линейных уравнений

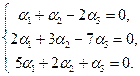
Заметим, что формулы Крамера для системы двух уравнений, справедливы и для любой линейной системы n уравнений с n неизвестными. Если определитель системы то система имеет единственное решение, определяемое формулами Крамера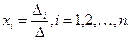

Вычислим определитель нашей системы

Определители – равны нулю, т.к. имеют нулевые столбцы, поэтому система имеет только нулевое решение Следовательно данные векторы линейно независимые.

Дата добавления: 2014-01-05