Конечноразностные интерполяционные формулы

Пусть функция у = f(x) задана на сетке равноотстоящих узлов x_i = x₀ + ih, где i = 0, 1,..., n, и для нее построена таблица конечных разностей.

В соответствии с тем, что было сказано о направлении модификации интерполяционной формулы Лагранжа в начале предыдущего параграфа, будем строить интерполяционный многочлен Р_n(x) в форме

P_n(x) = a₀ + a₁(x – x₀) + a₂(x – x₀)(x – x₁) +... +

+ a_n(x – x₀)(x – x₁)...(x – x_n–1). (14)

Его n + l коэффициент a₀, a₁,..., a_n будем находить последовательно из n + 1 интерполяционных равенств

P_n(x_i) = y_i, i = 0, 1, …, n.

А именно, полагая i = 0, т. е. x = x₀, в (14) имеем P_n(x₀) = a₀, а по условию интерполяции P_n(x₀) = y₀, следовательно, a₀ = y₀.

Далее, при i = 1 аналогично получаем равенство

a₀ + a₁(х₁ – х₀) = y₁,

в которое подставляем уже найденное значение a₀ = y₀. Разрешая это равенство относительно а₁ и используя обозначение конечной разности, получаем

.

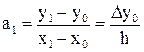Следующий шаг, при i = 2, дает:

a₀ + a₁(x₂ – x₀) + a₂(x₂ – x₀)(x₂ – x₁) = y₂ Û

Û

(см. (13) при k = 2).

Полной индукцией можно показать справедливость выражения

"k Î {1, 2, …, n}. (15)

Подставляя найденные коэффициенты a₀, a₁,..., a_n в (14), получаем многочлен

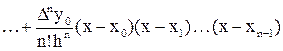, (16)

который называют первым интерполяционным многочленом Ньютона.

Учитывая, что каждое слагаемое многочлена (16), начиная со второго, содержит множитель x – x₀, естественно предположить, что этот многочлен наиболее приспособлен для интерполирования в окрестности узла x₀ (при x, близких к x₀, f(x)» y₀). Будем называть узел x₀ базовым для многочлена (16), и упростим (16) введением новой переменной q равенством , или (что то же) равенством x = x₀ + qh. Так как при любых i Î {0, 1, …, n}

x – x_i = x₀ + qh – x₀ – ih = h(q – i),

то в результате подстановки этих разностей в (16) приходим к первой интерполяционной формуле Ньютона в виде

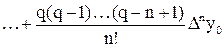, (17)

где обозначение P_n(x₀ + qh) указывает не только на n-ю степень многочлена, но и на базовый узел x₀ и связь переменных x и q.

Первая формула Ньютона (17) обычно применяется при значениях |q| < 1, а именно, для интерполирования вперед, (при x Î (x₀; x₁), т. е. при q Î (0; 1)) и экстраполирования назад (при x < x₀, т. е. при q < 0).

Так как реально степени интерполяционных многочленов бывают не так велики, в то время как таблицы значений функций достаточно обширны, и так как в реальной числовой таблице никаких индексов — номеров узлов нет, то за базовый для формулы (17) узел x₀ можно принимать узел, ближайший к заданной фиксированной точке x, если за ним имеется достаточное число узлов для построения необходимых для (17) разностей. Поскольку в первой формуле Ньютона используются нисходящие диагонали таблицы конечных разностей, то такое смещение узла, принимаемого за базовый, в конце таблицы будет неприемлемо.

Учет этого обстоятельства приводит к потребности в симметричной, в определенном смысле, для (17) формулы, которая была бы пригодной для интерполирования в конце таблицы. Для этого, в отличие от (14), форма интерполяционного многочлена P_n(x) берется такой, которая предусматривает поочередное подключение узлов в обратном порядке: сначала последний, потом предпоследний и т. д., т. е.

P_n(x) = a₀ + a₁(x – x_n) + a₂(x – x_n)(x – x_n–1) + … +

+ a_n(x – x_n)(x – x_n–1)...(x – x₁).

Коэффициенты a₀, a₁,..., a_n этого многочлена находятся аналогично тому, как они находились для многочлена (14), только здесь подстановка узловых точек вместо x и рассмотрение интерполяционных равенств производится тоже в обратном порядке. Полагая x = x_n, x = x_n–1,..., имеем:

Р_n(x_n) = a₀ = у_n,

,

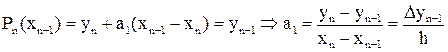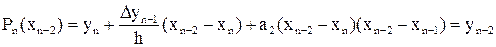
и т. д. В общем случае

"k Î {1, 2, …, n}.

Таким образом, получаем второй интерполяционный многочлен Ньютона

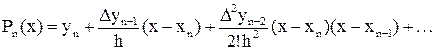
, (18)

в котором базовым является узел x_n и коэффициенты которого определяются конечными разностями, расположенными на восходящей от у_n диагонали.

Положим в (18) x = x_n + qh, иначе, введем новую переменную 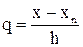и преобразуем к ней входящие в (18) разности:

x – x_i = x_n + qh – x₀ – ih = x₀ + nh + qh – x₀ – ih = h(q + n – h).

В результате приходим ко второй интерполяционной формуле Ньютона вида

. (19)

Ее также целесообразно использовать при значениях |q| < 1, т. е. в окрестностях узла x_n для интерполирования назад (при q Î (–1; 0)) и экстраполирования вперед (при q > 0).

Дата добавления: 2014-01-05