Гармонические колебания

Механические волны

Е) Вынужденные колебания. Резонанс.

Гармонические колебания

План лекции

Механические колебания и волны.

ЛЕКЦИЯ 1

а) Общая характеристика и уравнение колебательного движения

б) Баланс энергии при колебательном движении

в) Сложение гармонических колебаний

г) Гармонический спектр простого и сложного колебания

д) Затухающие колебания

а) Общая характеристика волны. Волны продольные и поперечные.

б) Уравнение плоской волны

в) Поток энергии волны. Уравнение Умова.

а) Общая характеристика и уравнение колебательного движения.

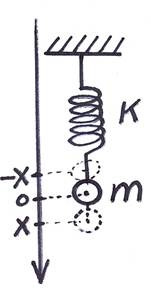
Колебательное движение – один из видов механического движения. В жизни оно встречается повсюду: маятник в настенных часах, груз, подвешенный на пружине, вода в открытом сосуде, вагон на рессорах, корабль на волнах и др. Главной характерной чертой колебательного движения является его повторяемость, т.е. каждое последующее движение повторяет предыдущее.

Для осуществления колебательного движения необходимы следующие условия: во-первых, должно быть наличие инертной массы, во-вторых, при выведении тела из положения равновесия должна возникать возвращающая сила. Данная сила должна быть пропорциональна величине отклонения тела от положения равновесия. Данная сила сообщает телу ускорение.

F = -kX - сила упругости; F = ma - сила инерции.

В данном случае, сила упругости является силой инерции: ma = -kX

Отсюда: a = -(k/m)X Введём обозначение: k/m = w² Здесь w - циклическая частота колебаний. Перепишем это уравнение в виде:

d²X/dt² = -w²X

Это – дифференциальное уравнение 2-го порядка. Представим его в виде:

d²X/dt² + w²X = 0

где d²X/dt² = kX/m w = k/m

Частное решение этого уравнения будет выглядеть так:

X = A sin (wt + fо)

Здесь:

X - текущая координата

A - амплитуда

w - циклическая частота

t - время

f - фаза

fо - начальная фаза.

Следует напомнить, что здесь, как и во всей физике принято координату и амплитуду измерять в метрах, время – в секундах, фазу – в радианах, циклическую частоту – в с^-1.

Кроме того, в физике колебательного движения приняты следующие единицы:

n - частота (Гц)

Т - период (с)

Частота (в герцах) показывает, сколько колебаний совершит тело за 1 секунду.

Частота w (в с^-1) показывает, сколько колебаний тело совершит за 2p секунд.

Период Т показывает продолжительность одного полного колебания (в секундах)

Особенность колебательного движения в том, что его легко можно связать с вращательным. Если представить себе какое-либо тело, движущееся по окружности в плоскости чертежа, то тень от него, падающая на вертикальную ось координат Х, будет совершать колебания вверх-вниз и если развернуть это движение на горизонтальную ось t, то получится кривая, являющаяся синусоидой.

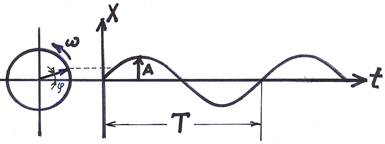
Следует заметить, что графиком частного решения вышеуказанного дифференциального уравнения является кривая той же формы:

Наибольшее затруднение у студентов вызывает понятие фазы. В колебательном движении фаза играет туже роль, что координата в поступательном движении.

Сравним:

X = (ut + X) для поступательного движения

f = (wt + f) для колебательного движения

В колебательном движении фаза показывает, какая часть периода прошла от начала колебания.

Зная, что координата колеблющегося тела изменяется по закону:

Х = А sin (wt + f)

найдём закон, по которому изменяется скорость и ускорение:

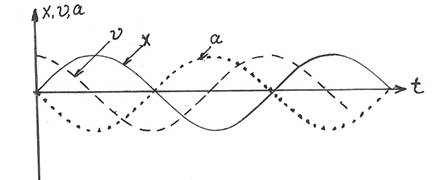
u = X^\ = A w cos(wt + f)

a = u ^\ = X^\\ = -Aw²sin (wt + f)

Отсюда видно, что координата, скорость и ускорение изменяются либо по закону синуса, либо по закону косинуса. Причём, производная любого порядка даст либо синус, либо косинус. Из этого следует, что синус и косинус являются гармоническими функциями. Значит движение, осуществляющееся по законам синуса или косинуса является гармоническим колебанием, или колебанием, типа «проще некуда».

Все эти три графика представляют собой кривую одинаковой формы, только эти кривые сдвинуты относительно друг друга на 90^о

б) Баланс энергии при колебательном движении

Следует напомнить формулы кинетической и потенциальной энергии, используемые в механике.

Ек = mu²/2 - кинетическая энергия

Еп = kX^2//2 - потенциальная энергия

Из закона сохранения энергии следует, что полная механическая энергия замкнутой системы – есть величина постоянная:

Ек + Еп = Е

u = dX/dt = (A sin wt)^\ = A cos wt u = Aw

a = d²X/dt² = du/dt (Acos wt)^\ = -Aw²sin wt a = Aw²

Кинетическая энергия точки:

Ek = mA² cos²w t

Потенциальная энергия точки:

Еп = kA²/2 здесь: k = m w² так как k = ma /X = mA²w ²/X

Итак:

Еп = mA² w ² sin² w t

Ек = mA² w² sin² w t

2

Ек + Еп = mA² w² (sin² wt + cos²wt)

Учитывая, что выражение в скобках равно единице, окончательно получим значение полной механической энергии колеблющейся точки

Е = mA² w²

в) Сложение гармонических колебаний

Гармонические колебания можно сложить как в одном направлении, так и во взаимно перпендикулярных направлениях. Рассмотрим сложение колебаний в одном направлении. Возьмём простейший случай, когда складываются колебания одинаковой частоты, совпадающих по фазе. В этом случае будут складываться их амплитуды:

Если складываются колебания, находящиеся в противофазе, то их амплитуды будут вычитаться. При одинаковых амплитудах, колебания вообще погасят друг друга:

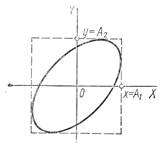
Если колебания складываются во взаимно перпендикулярном направлении, то колеблющаяся точка будет на плоскости выписывать сложную траекторию. Если частоты этих колебаний будут относиться как целые числа, то траектория будет иметь вид устойчивой кривой, которая называется фигурой Лиссажу:

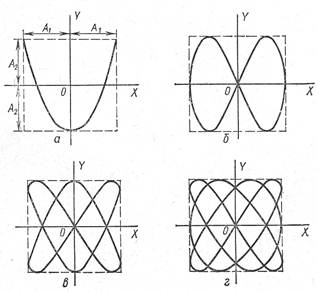
г) Гармонический спектр

Если в одном направлении складываются колебания разных частот, то точка будет совершать сложные колебания, график которых будет представлять очень замысловатый вид, изобразить который графически бывает очень трудно. Существует ещё один способ графического изображения колебательного движения.

Французский математик Фурье доказал, что периодический процесс любой формы можно разложить на простые гармонические колебания. В связи с этим, графически колебания можно изобразить гармоническим спектром. По горизонтальной оси откладывается частота, а по вертикальной – амплитуда. Таким образом, гармонический спектр простого синусоидального колебания представляет собой отрезок прямой, перпендикулярный оси частот. Положение отрезка по горизонтали определяется частотой, а длина отрезка – амплитудой колебания.

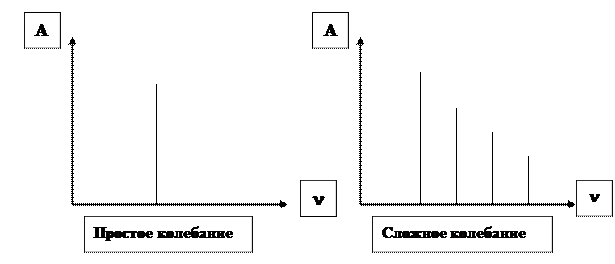
Спектр сложного колебания представляет собой несколько линий.

Во многих случаях колебания изображать гармоническим спектром удобнее и проще, чем их графиком.

д) Затухающие колебания

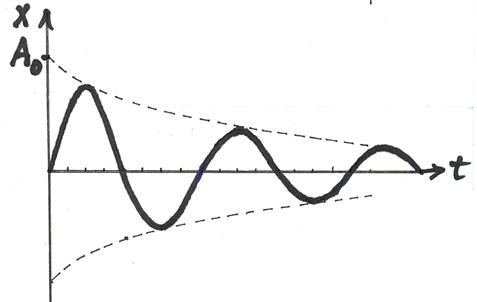
В идеальном случае в колебательной системе происходит обмен кинетической и потенциальной энергии, причём, потерь энергии на трение нет. Поэтому, амплитуда колебания остаётся постоянной. В реальных же условиях при каждом цикле часть энергии переходит во внутреннюю, поэтому амплитуда колебания постепенно уменьшается по экспоненциальному закону:

Х = Aoe^-bt sinwt гдe b - коэффициент затухания

График затухающего колебания имеет вид:

Дата добавления: 2014-01-05