Доопределение уравнений Максвелла в дифференциальной форме для проводящей материальной среды

Таким образом, мы получили систему уравнений Максвелла в дифференциальной форме для проводящей материальной среды:

УМ в дифференциальной форме проще исследовать аналитическими методами. Однако УМ (1.1)-(1.4) и (1.7),(1.8),(1.11),(1.12) незамкнуты. Действительно, рассмотрим УМ в дифференциальной форме. Имеем 2 векторных и 2 скалярных уравнения, т.е. 8 скалярных. Неизвестные: D, E, B, H, j^e,r^e –16 скалярных неизвестных (определяем число неизвестных и уравнений в скалярной форме). То есть уравнений для определения неизвестных нехватает: система недоопределена. Сколько еще нужно уравнений? 8? Нет, еще больше, так как уравнение (1.12) есть следствие уравнения (1.8). Действительно, если применить операцию div к уравнению (1.8), то получим откуда следует div B= 0. Таким образом, фактически имеем 7 скалярных уравнений, и чтобы система была замкнутой (число неизвестных=числу уравнений), необходимо добавить 9 уравнений. Эти уравнения вводятся обычно феноменологически и определяют связь векторов D, B, j ^eс E и H через материальные параметры среды. Поэтому эти уравнения называются материальными. В наиболее общей форме можно записать материальные уравнения (МУ) как

D = D (E,H), B= B (E,H), j^e=j^e(E,H).

После того, как МУ сформулированы, система УМ и МУ становится замкнутой. Формулируя МУ, вводят в рассмотрение определенный круг физических явлений, происходящих в реальных средах при взаимодействии с ними электромагнитного поля. Более подробно вопрос о МУ рассматривается в курсе «Радиофизика», читаемый кафедрой ОРТ. Используем далее следующую простейшую систему МУ

D =e _a E, (1.13) B= m _a H, (1.14) j ^e = s_e E. (1.15)

В (1.13) - (1.15) - e _a =e₀e- абсолютная диэлектрическая проницаемость среды, e₀- электрическая постоянная (абсолютная диэлектрическая проницаемость вакуума), e - относительная диэлектрическая проницаемость среды, m _a =m₀m - абсолютная магнитная проницаемость среды, m₀- магнитная постоянная (абсолютная магнитная проницаемость вакуума), m - относительная магнитная проницаемость среды, s_э - удельная объемная электрическая проводимость среды. Все параметры, входящие в (1.13)-(1.15): e _a, m _a, s_e, будем в простейшем случае считать константами.

Связи (1.13)-(1.15) соответствуют линейной изотропной среде. Линейность означает, что, например, вектор электрической индукции зависит только от электрического поля в первой степени. Изотропия означает, что вектор D параллелен вектору E независимо от ориентации последнего в среде (коэффициент пропорциональности e _a – скалярная величина). Если параметры среды e, m, s_e постоянны по объему среды, среда является пространственно однородной. Если параметры среды e,m,s_e не зависят от времени, среда является однородной во времени. Наконец, согласно (1.13)-(1.15) электрическая (магнитная) индукция и ток проводимости мгновенно отслеживают изменение электрического (магнитного) поля в среде, то есть среда является безынерционной. Таким образом, МУ (1.13) - (1.15) определяют линейную, изотропную, однородную, безынерционную среду.

Обсуждение более сложных материальных уравнений

(Здесь и далее мелким шрифтом выделен дополнительный материал, не обязательный, но желательный для изучения)

Усложнение МУ позволяет описать более тонкие физические явления. Поясню на примере МУ для электрической индукции.

Пространственная и временная неоднородность среды. Материальное уравнение D =e_a(r, t ) E -диэлектрическая проницаемость среды зависит от координат и времени.

Анизотропия. Материальное уравнение в декартовой системе координат запишем в виде D_i =e _aijE_{j ,} i,j= 1,2,3. Вектор электрической индукции не совпадает по направлению с вектором электрического поля. Связь между векторами D и E определяется тензором диэлектрической проницаемости <e_a > с компонентами e_{a ij} (в данном случае тензор – это матрица размерностью 3*3, связывающая векторы D и E)

Нелинейность. Нелинейные эффекты могут быть учтены при введении в зависимость D =e _a E квадратичных и более высоких степеней электрического поля. Например, представим D ( E ) рядом

D_i =e _aE_i +a _ijE_iE_j +b _ijkE_iE_jE_k +…..

Это МУ учитывает квадратичные и кубичные нелинейные эффекты по электрическому полю, которые приводят к генерации гармоник и возникновению комбинационных частот.

Инерционность среды. Материальное уравнение в инерционной среде можно представить в виде

.

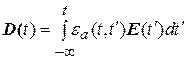Из вида МУ следует, что величина электрической индукции зависит не только от электрического поля в данный момент времени, но и от величины поля в предыдущие моменты времени (учитывается предыстория процесса). Зависимость e _a не только от текущего времени t, но и от предыдущих моментов времени t¢ означает, что имеет место явление временной дисперсии.

Наиболее общая формулировка МУ для линейной среды имеет вид:

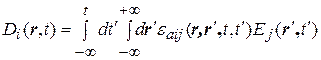
Здесь учтена не только временная, но и пространственная дисперсия среды, которая проявляется в следующем: e _a зависит не только от свойств среды в данной точке пространства r, но и в соседних точках пространства r ¢. Таким образом, электрическая индукция в точке пространства r зависит от значений электрического поля как в точке r, так и в соседних точках r ¢.

Существует два способа получения МУ. 1). Формулировка МУ из эвристических (феноменологических) соображений (примеры эвристических формулировок МУ приводились выше). В этом случае и структура МУ, и количественные значения коэффициентов МУ должны быть оправданы сопоставлением с экспериментом. 2) Вывод МУ путем совместного анализа УМ на микроуровне и уравнений квантовой теории вещества, либо анализа УМ совместно с макроскопическими уравнениями вещества. Так, для макроскопического описания плазмы используют кинетические либо гидродинамические уравнения, для твердого тела – уравнения теории упругости.

В нашем курсе будут использованы относительно простые виды МУ. Но следует запомнить, что выбор МУ должен быть адекватен кругу описываемых явлений. Если вы анализируете процессы в веществе, хорошо изученном в определенном частотном диапазоне, то и МУ для него известны. Если вы занимаетесь исследованиями взаимодействия ЭМ волн с веществом в неизученной ранее области, ставьте вопрос об адекватности используемых вами МУ вашей физической ситуации.

Рассмотрим далее систему УМ (1.7),(1.8),(1.11),(1.12) и МУ (1.13)-(1.15). Эта система замкнута (число уравнений равно числу неизвестных). Может возникнуть вопрос: почему нет МУ, определяющего связь плотности заряда r^э с полем? В нем нет необходимости, так как плотность заряда связана с током уравнением непрерывности. Уравнение непрерывности следует из уравнений (1.7) и (1.11). Подействуем оператором div на уравнение (1.7): divrot H = div (j ^e +¶ D/ ¶ t)=0. Отсюда следует, что div j ^e = –¶(div D)/ ¶ t. Так как div D= r ^e, получаем

div j ^e + ¶r ^e / ¶t= 0. (1.16)

Это и есть уравнение непрерывности, связывающее объемные плотности тока и заряда.

Замечание. Можно ввести уравнение непрерывности в число постулатов при формулировке УМ. Уравнение непрерывности легко выводится из физических соображений из анализа движения зарядов в трубке тока (см. кн Г.Т.Марков, Б.М.Петров, Г.П.Грудинская, Электродинамика и распространение радиоволн. М. 1979). При этом уравнение (1.11) будет следствием (1.7) и (1.16). Мы взяли в качестве исходной систему (1.7), (1.8), (1.11), (1.12). При этом (1.16) есть следствие (1.7) и (1.11).

Система УМ (1.7),(1.8),(1.11),(1.12) и МУ (1.13)-(1.15) самосогласована: движение зарядов (изменение тока) приводит к изменению полей D, B, E, H и к влиянию их на заряды (токи) и т.д. Возникает вопрос: как найти поля, токи и заряды из самосогласованных уравнений, если поля, токи и заряды влияют друг на друга? Ведь любое изменение полей вызовет обратное влияние полей на себя?

Выход из этого замкнутого круга в макроскопической электродинамике находят с помощью следующего эвристического приема: выделяют некоторые токи и заряды, которые считают сторонними источниками поля.

Дата добавления: 2014-01-05