Шифрование по алгоритму Шамира

157, 163, 167, 173, 179, 181, 191, 193, 197, 199.

Разложение числа на простые множители

ВОПРОСЫ ДЛЯ ПРОВЕРКИ

1. Каким было ударение в общеиндоевропейском языке?

2. Как изменилось индоевропейское ударение в общегерманском языке?

3. Что представляла собой система гласных фонем в общеиндоевропейском?

4. Как была выстроена система согласных фонем в общеиндоевропейском?

5. Как изменились системы гласных и согласных фонем в общегерманском?

6. Как изменилась индоевропейская морфологическая структура слова в общегерманском?

7. Какие основные грамматические категории известны Вам в индоевропейском?

8. Как изменились основные индоевропейские грамматические категории в общегерманском?

9. Какая германская лексика является по своему происхождению общеиндоевропейской?

Всякое составное число может быть единственным образом представлено в виде произведения простых множителей. Например,

48 = 2 · 2 · 2 · 2 · 3, 225 = 3 · 3 · 5 · 5, 1050 = 2 · 3 · 5 · 5 · 7.

Для небольших чисел это разложение легко делается на основе таблицы умножения. Для больших чисел рекомендуем пользоваться следующим способом, который рассмотрим на конкретном примере. Разложим на простые множители число 1463. Для этого воспользуемся таблицей простых чисел:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43,

47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101,

103, 107, 109, 113, 127, 131, 137, 139, 149, 151,

Перебираем числа по этой таблице и останавливаемся на том числе, которое является делителем данного числа. В нашем примере это 7. Делим 1463 на 7 и получаем 209. Теперь повторяем процесс перебора простых чисел для 209 и останавливаемся на числе 11, которое является его делителем (см. параграф “Признаки делимости”). Делим 209 на 11 и получаем 19, которое в соответствии с этой же таблицей является простым числом. Таким образом, имеем: 1463 = 7 ∙ 11 ∙ 19, т.е. простыми делителями числа 1463 являются 7, 11 и 19. Описанный процесс можно записать следующим образом:

Делимое Делитель
----------------------------
1463 7
209 11
19 19
----------------------------

1.1 Шифросистема RSA

Система RSA в настоящее время является наиболее распространенной системой шифрования с открытым ключом.

Возможность гарантированно оценить защищенность алгоритма RSA стала одной из причин популярности этой СОК на фоне десятков других схем. Поэтому алгоритм RSA используется в банковских компьютерных сетях, особенно для работы с удаленными клиентами (обслуживание кредитных карточек).

Рассмотрим математические результаты, положенные в основу этого алгоритма.

Теорема 1. (Малая теорема Ферма.)

Если р – простое число, то

x^p-1 = 1(mod p) (1)

для любого х, простого относительно р, и

x^p = x(mod p) (2)

для любого х.

Доказательство. Достаточно доказать справедливость уравнений (1) и (2) для x^p. Проведем доказательство методом индукции.

Очевидно, что уравнение (3) выполняется при х=0 и 1. Далее

x^p = (x –1 + 1)^p = C(p,j)(x –1)^j = (x –1)^p + 1(mod 2),

так как C(р,j)=0(mod р) при 0<j<р. С учетом этого неравенства и предложений метода доказательства по индукции теорема доказана.

Определение. Функцией Эйлера φ(n) называется число положительных целых, меньших n и простых относительно n.

n
φ(n)

Теорема 2. Если n = рq, (р и q – отличные друг от друга простые числа), то

φ(n)=(р-1)(q-1)

Теорема 3. Если n = рq, (р и q - отличные друг от друга простые числа) и х – простое относительно р и q, то

x^φ(n) = 1(mod n)

Следствие. Если n = рq, (р и q - отличные друг от друга простые числа) и е простое относительно (n), то отображение

E_е,n : xx^е(mod n)

является взаимно однозначным на Z_n.

Очевиден и тот факт, что если е – простое относительно f(n), то существует целое d, такое, что

ed ≡ 1 (mod φ(n)) (3)

На этих математических фактах и основан популярный алгоритм RSA.

Пусть n = рq, где р и q – различные простые числа. Если e и d удовлетворяют уравнению, то отображения Е_e,n и Е_d,n являются инверсиями на Z_n. Как Е_e,n, так и Е_d,n легко рассчитываются, когда известны e, d, р, q. Если известны e и n, но р и q неизвестны, то Е_e,n представляет собой одностороннюю функцию; нахождение Еd,n по заданному n равносильно разложению n. Если р и q – достаточно большие простые, то разложение n практически не осуществимо. Это и заложено в основу системы шифрования RSA.

1.1 Шифросистема RSA

Система RSA в настоящее время является наиболее распространенной системой шифрования с открытым ключом.

Пусть n = pq – целое число, представляемое в виде произведения двух больших простых чисел p, q. Числа e и d, определяющие алгоритмы шифрования и расшифрования соответственно, должны отвечать условию

ed ≡ (mod φ(n)), (1)

где φ(n) = (p-1)(q-1) – значение функции Эйлера от числа n. Пусть k = (n,p,q,e,d) – выбранный ключ, состоящий из открытого ключа k1 = (n,e) и секретного ключа k2 = (n,p,q,d). Пусть M – блок открытого текста и C – соответствующий блок шифрованного текста. Тогда правила шифрования и расшифрования определяются формулами:

С = E_k (M) =M^e (mod n), D_k(C) = C^d (mod n) (2)

Заметим, что в соответствии с (2) D_k(C) = M

При нахождении значений e и d, удовлетворяющих условию (1), значение e обычно задают таким образом, чтобы оно было взаимнопростым с φ(n), а значение d определяют из уравнения

φ(n)x + ed = 1 (3)

В общем случае уравнение (3) имеет вид ax + by = c (здесь a = φ(n), b = e, y = d) и называется Диафантовым уравнением.

Решение этого уравнения

y = (–1)^μ · a_μ-1 · x = (–1)^μ+1 · b _μ-1 (4)

можно получить с помощью разложения отношения a/b в цепную дробь:

где μ – порядок цепной дроби, т.е. индекс коэффициента дроби, у которого остаток равен нулю,

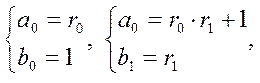
(5)
а для всех членов, начиная с третьего справедливо

(6)

Таким образом, для решения уравнения (3) необходимо представить отношение a/b в виде цепной дроби, определить при этом значения r₀, r₁…r_μ и μ. Потом в соответствии с (4) – (6) определяются значения a_i, b_i, а также x и y.

На этих математических фактах и основан популярный алгоритм RSA.

Пусть n = рq, где р и q – различные простые числа. Если e и d удовлетворяют уравнению (8.2.3), то отображения Еe,n и Еd,n являются инверсиями на Zn. Как Еe,n, так и Еd,n легко рассчитываются, когда известны e, d, р, q. Если известны e и n, но р и q неизвестны, то Еe,n представляет собой одностороннюю функцию; нахождение Еd,n по заданному n равносильно разложению n. Если р и q – достаточно большие простые, то разложение n практически не осуществимо. Это и заложено в основу системы шифрования RSA.

Пользователь i выбирает пару различных простых рi и qi и рассчитывает пару целых (ei, di), которые являются простыми относительно ц(ni), где n = рi qi. Справочная таблица содержит публичные ключи {(ei,ni)}.

Предположим, что исходный текст

x =(x0, x1,..., xn-1), xZn, 0 i < n,

сначала представлен по основанию ni:

N = c0+ci ni+....

Пользователь i зашифровывает текст при передаче его пользователю j, применяя к n отображение Edi,ni:

N Edi,ni n = n'.

Пользователь j производит дешифрование n', применяя Eei,ni:

N' Eei,ni n'= Eei,ni Edi,ni n = n.

Очевидно, для того чтобы найти инверсию Edi,ni по отношению к Eei,ni, требуется знание множителей n = рi qi. Время выполнения наилучших из известных алгоритмов разложения при n = 10^100 на сегодняшний день выходит за пределы современных технологических возможностей.

Рассмотрим небольшой пример, иллюстрирующий применение алгоритма RSA.

Пример Зашифруем сообщение "САВ". Для простоты будем использовать маленькие числа (на практике применяются гораздо большие).

1. Выберем р=3 и q=11.

2. Определим n=3*11=33.

3. Найдем (р-1)(q-1) = 20. Следовательно, в качестве d, взаимно простое с 20, например, d=3.

4. Выберем число е. В качестве такого числа может быть взято любое число, для которого удовлетворяется соотношение (е*3) (mod 20) = 1, например 7.

5. Представим шифруемое сообщение как последовательность целых чисел с помощью отображения: А1, В2, С3. Тогда сообщение принимает вид (3,1,2). Зашифруем сообщение с помощью ключа {7,33}.

6. Расшифруем полученное зашифрованное сообщение (9,1,29) на основе закрытого ключа {3,33}:

Итак, в реальных системах алгоритм RSA реализуется следующим образом: каждый пользователь выбирает два больших простых числа, и в соответствии с описанным выше алгоритмом выбирает два простых числа e и d. Как результат умножения первых двух чисел (р и q) устанавливается n.

{e,n} образует открытый ключ, а {d,n} – закрытый (хотя можно взять и наоборот).

Открытый ключ публикуется и доступен каждому, кто желает послать владельцу ключа сообщение, которое зашифровывается указанным алгоритмом. После шифрования, сообщение невозможно раскрыть с помощью открытого ключа. Владелец же закрытого ключа без труда может расшифровать принятое сообщение.

Зашифровать сообщение по алгоритму Шамира для трех абонентов, взяв значение сообщения m и значение p из таблицы №3. По номеру i (предпоследняя цифра) студент выбирает сообщение для зашифровывания, по j – требуемые для реализации этого алгоритма число р. Выбор данных для других абонентов произвести циклически согласно процедуре (I + 1) и (G + 1). Например, последние цифры номера зачетной книжки – (26). Выбираем для трех абонентов (сообщение, p) - (16,49), (18,51), (20,53).

Таблица №3 – исходные данные

I
Сообщение
G
p

I
Сообщение
G
p

Дата добавления: 2014-01-05