В-пятых, это так называемая дисперсия остатков

Этот показатель рассчитывается по формуле:

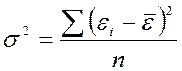, где

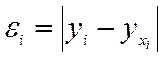- так называемые «остатки» уравнений регрессии, т.е. отклонения теоретических (расчетных) значений переменной y от ее фактических значений.

Наконец, это так называемый критерий Фишера, который позволяет оценить статистическую значимость самого индекса детерминации. Критерий Фишера рассчитывается по формуле:

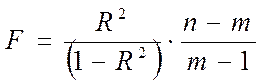
где n - число наблюдений (то есть известных значений всех переменных) или, что то же самое, длина ряда исходных статистических данных;

m – число параметров уравнения регрессии.

Число параметров, как правило, на единицу больше числа переменных (хотя из этого общего правила могут быть исключения).

Например, в уравнении двухфакторной линейной регрессии 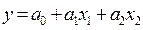три параметра: 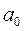,,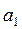 , 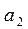то есть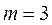

Расчетное значение 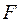сравнивается с табличным при количестве степеней свободы: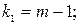

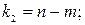
Наконец, имеется еще такой специальный показатель, как критерий Стьюдента, который используется не для оценки значимости всего уравнения в целом, а отдельных параметров уравнения регрессии. Критерий Стьюдента может использоваться в качестве дополнительного критерия отбора факторов, которые целесообразно включить в модель регрессии. Значимость отдельного параметра уравнения регрессии характеризует то, насколько случайным является отличие данного параметра от нуля.

Таким образом, если оказалось, что параметр 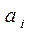при переменной 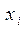не является значимым, то это значит, что фактор 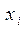не играет важной роли, и целесообразно исключить его из уравнения, то есть построить новое уравнение регрессии без этого фактора.

Обычно в уравнении множественной линейной регрессии значения критерия Стьюдента рассчитываются по формулам:

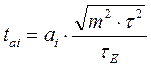, для любого параметра, кроме a₀, а для параметра a₀ этот критерий определяется по формуле:

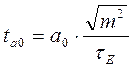
Расчетное значение критерия Стьюдента (так же, как и значение критерия Фишера) сравнивается с табличным. Если расчетное значение превышает табличное, то данный параметр считается значимым.

Далее мы остановимся на содержательном смысле критерия Фишера и критерия Стьюдента более подробно.

2й учебный вопрос: Общие правила проверки статистических гипотез.

Обычно в выборочных наблюдениях, как известно из курса теории статистики, оценку генерального параметра получают на основе выборочного показателя с учетом ошибки репрезентативности. Ошибка выборки – это разница между значениями показателя, полученного по выборке и генеральным параметром. В другом случае в отношении свойств генеральной совокупности выдвигается некоторая гипотеза о величине средней, дисперсии, характере распределения, форме и тесноте связи между переменными. Проверка гипотезы осуществляется на основе выявления согласованности эмпирических данных с гипотетическими (теоретическими). Если расхождение между сравниваемыми величинами не выходит за пределы случайных ошибок, гипотезу принимают. При этом не делается никаких заключений о правильности самой гипотезы, речь идет лишь о согласованности сравниваемых данных. Основой проверки статистических гипотез являются данные случайных выборок. При этом безразлично, оцениваются ли гипотезы в отношении реальной или гипотетической генеральной совокупности. Последнее открывает путь применения этого метода за пределами собственно выборки: при анализе результатов эксперимента данных сплошного наблюдения, но малой численности. В этом случае рекомендуется проверить, не вызвана ли установленная закономерность стечением случайных обстоятельств, насколько она характерна для того комплекса условий, в которых находится изучаемая совокупность.

Статистической гипотезой (обозначается Н) называется предположение о свойстве генеральной совокупности, которое можно проверить, опираясь на данные выборки. Так, может быть выдвинута гипотеза о том, что средняя 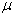в генеральной совокупности равна некоторой величине а (записывается Н: 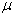= а) или о том, что генеральная средняя больше некоторой величины (Н: 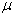> в).

Различают простые и сложные гипотезы. Гипотеза называется простой, если она однозначно характеризуется параметром распределения случайной величины. Например, Н: 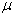= а.

Сложная гипотеза состоит из конечного или бесконечного числа простых гипотез, при этом указывается некоторая область вероятных значений параметра. Например, Н: 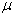> в. Эта гипотеза состоит из множества простых гипотез Н: 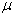= с, где с – любое число, большее в.

Гипотезы о параметрах генеральной совокупности называются параметрическими, о распределениях – непараметрическими. Гипотеза о том что две совокупности сравниваемые по одному или нескольким признакам, не отличаются, называется нулевой гипотезой или нуль-гипотезой (обозначается Н₀). При этом предполагается, что действительное различие сравниваемых величин равно нулю, а выявленное по данным отличие от нуля носит случайный характер. Например, Н₀: 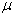₁ = 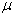₂ и т.д.
Нулевая гипотеза отвергается тогда, когда по выборке получается результат, который при истинности выдвинутой нулевой гипотезы маловероятен. Границей невозможного или маловероятного обычно считают 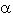= 0,05, т.е. 5% или 0,01, 0,001. Если ориентироваться на правило «трех сигм» (оно состоит в следующем: 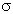= 1/6(х_mах - х_min), так как в нормальном распределении в размахе вариации «укладывается» 6 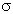(±3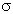)), то вероятность ошибки a должна быть равна 0,0027. Однако для этого уровня вероятности ошибки значений критериев редко табулируются: как правило, значения критериев в статистико-математических таблицах рассчитаны для вероятностей ошибки 0,05; 0,01; 0,001.

Статистическим критерием называют определенное правило, устанавливающее условия отклонения проверяемой нулевой гипотезы. Проверка статистических гипотез состоит из следующих этапов:

· формулируется в виде статистической гипотезы задача исследования;

· выбирается статистическая характеристика гипотезы;

· выбираются испытуемая и альтернативная гипотезы на основе анализа возможных ошибочных явлений и их последствий;

· определяется область допустимых значений, критическая область, а также критическое значение статистического критерия (t; F; 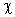²) по соответствующей таблице;

· вычисляется фактическое значение статистического критерия;

· проверяется гипотеза на основе сравнения фактического и критического значений критерия, и в зависимости от результатов проверки гипотеза либо отклоняется, либо не отклоняется.

При проверке гипотез по одному из критериев возможны 2 ошибочных решения:
- неправильное отклонение Н₀: ошибка 1-го рода;
- неправильное принятие Н₀: ошибка 2-го рода.
В то время, как фактически Н₀ верна (1) и Н₀ не верна (2), принимают 2 ошибочных решения:

- Н₀ отклоняется и принимается альтернативная гипотеза;

- Н₀ не отклоняется

Вероятности, соответствующие неверным решениям, называется риском 1 и риском 2. Риск 1 равен вероятности ошибки α (уровню значимости), риск 2 равен вероятности ошибки β. Поскольку α всегда больше 0, то всегда есть риск ошибки β. Обычно задают значение α и пытаются сделать возможно β малым. Вероятность 1-β называется мощностью критерия: чем она больше, тем меньше вероятность ошибки 2-го рода.

Альтернативная гипотеза Н₁ может быть сформулирована по-разному в зависимости от того, какие отклонения от гипотетической величины нас особенно беспокоят: положительные, отрицательные либо и те, и другие. Соответственно альтернативные гипотезы могут быть записаны как:
Н₁: 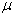> а, Н₁: 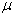< а, Н₁: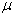 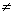а

3й учебный вопрос: Оценка значимости уравнений регрессии с помощью критерия Фишера.

После построения уравнения линейной регрессии, проводится оценка значимости как уравнения в целом, так и отдельных его параметров. Проверить значимость уравнения регрессии – значит установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной. Оценка значимости уравнения регрессии в целом дается с помощью F-критерия Фишера. При этом выдвигается нулевая гипотеза, что коэффициент регрессии равен нулю, следовательно, фактор х не оказывает влияния на результат у.

Величина F–отношения (F-критерий) получается при сопоставлении факторной и остаточной дисперсии в расчете на одну степень свободы.

F = D_факт / D_ост (5.5)

F-критерий проверки для нулевой гипотезы Н₀: D_факт = D_ост
Если нулевая гипотеза справедлива, то факторная и остаточная дисперсии не отличаются друг от друга. Для Н₀ необходимо опровержение, чтобы факторная дисперсия превышала остаточную в несколько раз. Английским статистиком Снедекором разработаны таблицы критических значений F-отношений при разных уровнях существенности нулевой гипотезы и различном числе степеней свободы. Табличное значение F-критерия – это максимальная величина отношения дисперсий, которая может иметь место при случайном их расхождении для данного уровня вероятности наличия нулевой гипотезы. Вычисленное значение F-отношения признается достоверным (отличным от 1), если оно больше табличного.

В этом случае нулевая гипотеза об отсутствии связи признаков отклоняется и делается вывод о существенности этой связи: F_факт > F_табл Н₀ отклоняется.

Если же величина оказалась меньше табличной F_факт < F_табл, то вероятность нулевой гипотезы меньше заданного уровня (например, 0, 05) и она не может быть отклонена без серьезного риска сделать неправильный вывод о наличии связи. В этом случае уравнение регрессии считается статистически незначимым и не отклоняется. Проверка значимости уравнения регрессии производится на основе дисперсионного анализа. В математической статистике дисперсионный анализ рассмотрен как самостоятельный инструмент (метод) статистического анализа. В эконометрике он применяется как вспомогательное средство для изучения качества модели. Центральное место в анализе дисперсии занимает разложение общей суммы квадратов отклонений переменной у от среднего значения у на 2 части - «объясненную» и «необъясненную»:

Общая сумма квадратов отклонений

=

Сумма квадратов отклонений, объясненная регрессией

+

Остаточная сумма квадратов отклонений

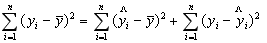(5.6)

или Q = Q _R + Q _e (5.7)

В переводной литературе обычно принято следующее обозначение:

TSS = RSS + ESS

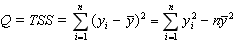- общая сумма квадратов отклонений; (5.8)

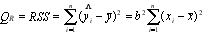– сумма квадратов отклонений, обусловленная регрессией; (5.9)

Q = ESS = 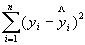– остаточная сумма квадратов отклонений. (5. 10)

Таблица 5.1

Схема дисперсионного анализа.

Средние квадраты и s_R² представляют собой несмещенные оценки зависимой переменной, обусловленных соответственно регрессией или объясняющей переменной х и воздействием неучтенных случайных факторов и ошибок; m – число оцениваемых параметров регрессии, n – число наблюдений. При отсутствии линейной зависимости между зависимой и объясняющей (факторной) переменной случайные величины и s_R² имеют ² – распределение соответственно с m-1 и n-m степенями свободы, а их отношение F – распределение с теми же степенями свободы. Поэтому, уравнение регрессии значимо на уровне , если фактически наблюдаемое значение статистики превышает табличное:

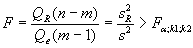(5.11),

где 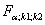- табличное значение F – критерия Фишера – Снедекора, определенное на уровне значимости 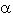при k1 = m-1 и k2 = n-m степенях свободы.

Учитывая смысл величин и s_R², можно сказать, что значение F показывает, в какой мере регрессия лучше оценивает значение зависимой переменной по сравнению с ее средней.

В случае парной линейной регрессии m = 2, и уравнение регрессии значимо на уровне 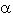, если

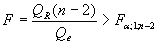(5.12)

Мерой значимости линии регрессии может служить следующее соотношение:

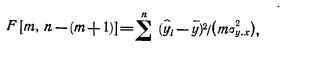
где ŷ_i—i-e выравненное значение; 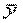—средняя арифметическая значений y_i; σ_y.x—средняя квадратическая ошибка (ошибка аппроксимации) регрессионного уравнения, вычисляемая по известной формуле; n—число сравниваемых пар значений признаков; m—число факторных признаков.

Действительно, связь тем больше, чем значительнее мера рассеяния признака, обусловленная регрессией, превосходит меру рассеяния отклонений фактических значений от выравненных.

Данное соотношение позволяет решить вопрос о значимости уравнения регрессии в целом, то есть о наличии реально существующей статистической зависимости между переменными. Уравнение регрессия значимо, т. е. между признаками существует статистическая связь, если для данного уровня значимости расчетное значение критерия Фишера F[m,n-(m+1)] превышает критическое значение F_кр[m,n-(m+1)], стоящее на пересечении m-го столбца и [n—(m+1)]-й строки специальной статистической таблицы, которая так и называется «Таблица значений F-критерия Фишера».

Пример. Воспользуемся критерием Фишера для оценки значимости уравнения регрессии, построенного на прошлой лекции, то есть уравнения, выражающего зависимость между сбором урожая и размером посева на душу населения.

Подставив в формулу для расчета критерия Фишера, данные предыдущего примера, получим

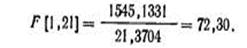
Обращаясь к таблице F-распределения для Р=0,95 (α=1—Р=0,5) и учитывая, что n-2=21, m-1 =1, в таблице значений F-критерия на пересечения 1-го столбца и 21-й строки находим критическое значение F_кр, равное 4,32 при степени надежности Р=0,95. Поскольку расчетное значение F-критерия существенно превосходит по величине F_кр, то обнаруженная линейная связь существенна, т. е. априорная гипотеза о наличии линейной связи подтвердилась. Вывод сделан при степени надежности P=0,95. Можно проверить, что вывод в данном случае останется прежним, если надежность повысить до Р=0,99 (соответствующее значение F_кр=8,02 для уровня значимости α=0,01).

Коэффициент детерминации. С помощью F-критерия мы установили, что существует линейная зависимость между величиной сбора хлеба и величиной посева на душу. Следовательно, можно утверждать, что величина сбора хлеба, приходящегося на душу, линейно зависит от величины посева на душу. Теперь уместно поставить уточняющий вопрос — в какой степени величина посева на душу определяет величину сбора хлеба на душу? На этот вопрос можно ответить, рассчитав, какая часть вариации результативного признака может быть объяснена влиянием факторного признака. Этой цели служит индекс (или коэффициент) детерминации R², который позволяет оценить долю разброса, учитываемого регрессией, в общем разбросе результативного признака. Коэффициент детерминации, равный отношению факторной вариации к полной вариации признака, позволяет судить о том, насколько «удачно» выбран вид функции, описывающей реальную статистическую зависимость.

Если известен коэффициент детерминации R², то критерий значимости уравнения регрессии или самого коэффициента детерминации (критерий Фишера) может быть записан в виде:

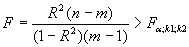
Критерий Фишера позволяет также оценивать полезность включения дополнительных факторов в модель для уравнения множественной линейной регрессии.

В эконометрике, помимо общего критерия Фишера, используется также понятие частного критерия. Частный F-критерий показывает степень влияния дополнительной независимой переменной на результативный признак и может использоваться при решении вопроса о добавлении в уравнение или исключении из него этой независимой переменной.

Разброс признака, объясняемый уравнением двухфакторной регрессии, построенным ранее, можно разложить на два вида: 1) разброс признака, обусловленный независимой переменной х₁, и 2) разброс признака, обусловленный независимой переменной x₂, когда х₁ уже включена в уравнение. Первой составляющей соответствует разброс признака, объясняемый уравнением, включающим только переменную х₁. Разность между разбросом признака, обусловленным уравнением парной линейной регрессии, и разбросом признака, обусловленным уравнением двухфакторной линейной регрессии, определит ту часть разброса, которая объясняется дополнительной независимой переменной x₂.

Отношение указанной разности к разбросу признака, регрессией не объясняемому, представляет собой значение частного критерия. Частный F-критерий называется также последовательным, если статистические характеристики строятся при последовательном добавлении переменных в регрессионное уравнение.

Пример. Оценить полезность включения в уравнение регрессии дополнительной переменной «урожайность» (по данным и результатам ранее рассмотренных примеров).

Разброс признака, объясняемый уравнением множественной регрессии и рассчитываемый как сумма квадратов разностей выравненных значений и их средней, равен 1623,8815. Разброс признака, объясняемый уравнением простой регрессии, составляет 1545,1331.

Разброс признака, регрессией не объясняемый, определяется квадратом средней квадратической ошибки уравнения и равен 10,9948.

Воспользовавшись этими характеристиками, рассчитаем частный F-критерий

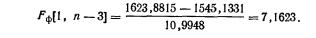
С уровнем надежности 0,95 (α=0,05) табличное значение F (1,20), т. е. значение, стоящее на пересечении 1-го столбца и 20-й строки табл. 4А приложения, равно 4,35. Рассчитанное значение F-критерия значительно превосходит табличное, и, следовательно, включение в уравнение переменной «урожайность» имеет смысл.

Таким образом, выводы, сделанные ранее относительно коэффициентов регрессии, вполне правомерны.

4й учебный вопрос. Оценка значимости отдельных параметров уравнения регрессии с помощью критерия Стьюдента.

Очень часто в эконометрике требуется оценить значимость коэффициента корреляции r, то есть определить, насколько существенно отличие коэффициента корреляции от нуля (например, при анализе мультиколлинеарности и оценке парных коэффициентов корреляции между факторами в уравнении множественной регрессии).

При этом исходят из того, что при отсутствии корреляционной связи статистика t,

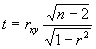
имеет t -распределение Стьюдента с (n-2) степенями свободы.

Коэффициент корреляции r_xy значим на уровне 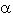, (иначе – гипотеза Н₀ о равенстве генерального коэффициента корреляции нулю отвергается), если

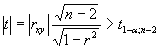(5.13),

где 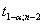-табличное значение t -критерия Стьюдента, определенное на уровне значимости a при числе степеней свободы (n-2).

В линейной регрессии обычно оценивается значимость не только уравнения в целом, но и отдельных его параметров. С этой целью по каждому из параметров определяется его стандартная ошибка. Процедура оценивания существенности данного параметра не отличается от рассмотренной выше для коэффициента регрессии; вычисляется значение t-критерия, его величина сравнивается с табличным значением при (n-2) степенях свободы. Проверка гипотез о значимости коэффициентов регрессии и корреляции равносильна проверке гипотезы о существенности линейного уравнения регрессии.

Заключение. Итак, мы рассмотрели на данной лекции общие правила проверки статистических гипотез и их практическое применение при оценке значимости уравнений регрессии и их отдельных параметров с помощью критериев Фишера и Стьюдента.

Дата добавления: 2014-01-05