Графическая интерпретация теории Кулона — Мора. Условие предельного равновесия

Приведенные выше положения наглядно иллюстрируются с помощью графического построения кругов напряжений Мора для предельного состояния. Пусть некоторый образец связного грунта испытывался в условиях плоской задачи (рис. 7.5, б) при постоянном значении минимального главного напряжения σ₃ — const так, чтобы при некотором значении максимального главного напряжения σ₁ наступило его разрушение, т. е. в нем сформировались площадки скольжения. В координатных осях г — а построим в соответствии с правилами курса сопротивления материалов круг напряжений Мора (рис. 7.6). Отложим на оси τ отрезок ОЕ, соответствующий сцеплению с данного грунта. Если теперь через точку Е провести касательную к кругу напряжений, пересекающуюся с осью σ, то получим графическое изображение прямой, соответствующей уравнению сопротивления сдвигу связного грунта (7.2).

Действительно, из треугольника О'АС' можно записать

АС' = О'С tg φ, т. е. τ_пр = ( σ + σ _c) tg φ,

что соответствует уравнению (7.3). Поскольку в соответствии с построениями на рис. 7.5 σ_c = с tg φ, отсюда легко получить зависимость

τ_пр = σ tg φ + c.

Можно также показать, что для любой точки на круге напряжений с координатами τ_α и σ_α, соответствующими напряжениям на наклонной площадке, не находящейся в предельном состоянии, угол отклонения Θ будет всегда меньше максимального угла отклонения Θmах= φ [см. уравнения (7.4) и (7.5)]. Также отметим, что прямая сопротивления сдвигу не может пересекать круг напряжений, так как иначе пришлось бы допустить, что Θ может быть больше φ или, что то же самое, τ может быть больше τ_пр, а это, как следует из рис. 7.4, физически невозможно.

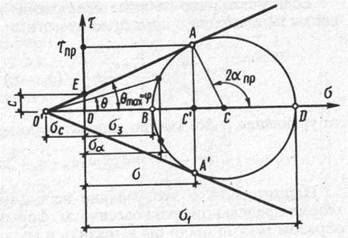
Рис. 7.6. Круг напряжений и график сопротивления сдвигу связного грунта в условиях плоской задачи

Точка касания А прямой сопротивления сдвигу к кругу напряжений определяет наклон площадки скольжения к направлению главных напряжений. Поскольку треугольник О'АС прямоугольный, имеем 180° – 2α_пр = 180° – (90° + φ). Отсюда получаем одно из двух условий выражения (7.9):

α_пр = π/4 + φ /2

Так как главные напряжения взаимно перпендикулярны, это определяет и второе условие

α_пр = π/4 – φ /2

Если же аналогичным образом рассмотреть и вторую касательную к кругу напряжений О'А' на рис. 7.6, все эти рассуждения можно использовать и для второй сопряженной площадки скольжения, показанной на рис. 7.5, в.

Из построений на рис. 7.6 легко получить следующее важное условие:

так как sin φ =АС/О'С, а О'С = О'О + ОВ+ВС, то, учитывая, что АС = ВС = (σ₁ – σ₃)/2;О'О = σ_с; ОВ= σ₃, имеем

sin φ = (σ₁ – σ₃)/((σ₁ + σ₃ + 2σ_с). (7.10)

Выражение (7.10) часто называют условием предельного равновесия связных грунтов, так как оно показывает предельное соотношение между главными напряжениями σ₁ и σ_3, при котором в данной точке массива грунта, характеризуемого параметрами прочности φ и c=actg φ, наступает состояние предельного равновесия. Очевидно, что для сыпучих грунтов, для которых с = 0, условие предельного равновесия будет иметь более простой вид:

sin φ = (σ₁ – σ₃)/((σ₁ + σ₃). (7.11)

Отметим, что если в какой-либо точке грунта имеет место такое соотношение главных напряжений, при котором правая часть уравнений (7.10) или (7.11) оказывается меньше величины sin φ данного грунта, это означает, что грунт в этой точке находится в допредельном состоянии по прочности. В этом нетрудно убедиться, построив соответствующий круг напряжений, так как он не будет касаться прямой сопротивления сдвигу. Соответственно условие, когда правая часть приведенных уравнений оказывается больше величины sin φ, физически невозможно, поскольку величина Θ не может быть больше φ.

Если учесть, что главные напряжения выражаются через компо­ненты напряжений с помощью известных зависимостей

σ₁ + σ₃ = (σ_x + σ_z) /2 + ½√((σ_x – σ_z)² + 4τ²_xz), (7.12)

то уравнение (7.10) можно записать в виде

(σ_x – σ_z)² + 4τ²_xz = (σ_x + σ_z +2 σ_с)² sin2 φ. (7.13)

Напомним, что это условие используется при решении задач теории предельного равновесия.

Дата добавления: 2014-01-05