
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Матрица неисправностей и вероятности состояний
|
|
|
|
Таб.16
| Si | Zi | Pi | |||||
| Z1 | Z2 | Z3 | Z4 | Z5 | Z6 | ||
| S1 | 0,2 | ||||||
| S2 | 0,05 | ||||||
| S3 | 0,24 | ||||||
| S4 | 0,15 | ||||||
| S5 | 0,06 | ||||||
| S6 | 0,3 |
Пусть первым контролируется параметр Z1. Тогда множество возможных состояний разбивается на два подмножества S0(Z1) и S1(Z1).Для подмножества S0(Z1) последовательность состояний вероятностей будет состоять из одного состояния Р(S1) =0,2, а подмножества S1(Z1) составим первую последовательность: Р(S2) = 0,05; Р(S5) =0,06; Р(S4) =0,15; Р(S3) =0,24; Р(S6) =0,3. Затем определим сумму двух наименьших вероятностей: Р*1 = 0,05 + 0,06 = 0,1.
Составим вторую последовательность: Р*1 = 0,1; Р(S4) = 0,15; Р(S3) =0,24; Р(S6) =0,03. Затем определим Р*2 = 0,11 + 0,15 = 0,26.
Составим третью последовательность: Р(S3) = 0,24; Р*2 = 0,26; Р(S6) =0,3. Затем определим Р*3 = 0,24 + 0,26 = 0,5.
И наконец, составим четвертую последовательность: Р(S6) =0,3; Р*3 = 0,5 и определим Р*4 = 0,3 + 0,5 = 0,8.
При этом нижняя граница средней стоимости
N 0 6-1-1
Сн(Z1) = С [ ∑ Р(Si) + ∑ Рλ + ∑ Р*ν] = C (1 +0 +1,67) = 2,67 C
i=1 λ=1 ν=1
Следует указать, что если подмножество S0(Zi) содержит одно состояние, то нижняя граница стоимости Сн(S1) = 0.
Разделение множества возможных состояний на два подмножества S0(Z1) и S1(Z1) при контроле параметра Z1 как показано в табл. 16.
При контроле параметра Z2 множество возможных состояний разбивается на два подмножества: S0(Z2) и S1(Z2) (табл. 17).
Таб.17
| Si | Zi | Pi | |||||
| Z1 | Z2 | Z3 | Z4 | Z5 | Z6 | ||
| S1 | 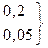 S0 (Z2) S0 (Z2)
| ||||||
| S2 | |||||||
| S3 | 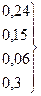 S0 (Z2) S0 (Z2)
| ||||||
| S4 | |||||||
| S5 | |||||||
| S6 |
Для подмножества S0(Z2) последовательность двух значений вероятностей будет из двух значений: Р(S2) = 0,05 и Р(S1) = 0,2, и тогда Р*1 = 0,05 + 0,2 = 0,25.
|
|
|
Для подмножества S1(Z2) первая последовательность будет иметь вид Р(S5) =0,06; Р(S4) =0,15; Р(S3) =0,24; Р(S6) = 0,3, и тогда Р*1 = 0,21; Р*2 = 0,45; Р*3 = 0,75.
Следовательно, нижняя граница средней стоимости при контроле параметра
N 0 6-1-1
Сн(Z2) = С [ ∑ Р(Si) + ∑ Рλ + ∑ Р*ν] = C (1 +0,25 +1,41) = 2,66 C.
i=1 λ=1 ν=1
Поступая аналогичным образом при контроле параметров z3 , z4 и z5, получим нижние границы стоимости при контроле соответствующих параметров: СН (z3 ) = 2,59C; СН (z4) = 2,60С; СН (z5) = 2,50С.
Из результатов вычислений нижних границ средней стоимости следует, что минимальной стоимостью будет обладать алгоритм поиска, начинающийся с контроля параметра z5.
Посмотрим матрицу (табл. 18) состояний подмножества:
S0 (z5) и S1 (z5).
Анализируя табл. 18, видим, что в случае отрицательного исхода при контроле параметра z5 следующими можно контролировать параметры z1 , z2 , z5. Параметр z3 контролировать не имеет смысла, так как подмножество S0(z5) не разбивает при его контроле на более мелкие подмножества. При положительном исходе можно контролировать параметры z3 , z4.
Таким образом, необходимо вычислить значения стоимостей нижних границ алгоритма поиска при контроле таких наборов параметров z5 , z1 , z3 , z5 , z1 , z5 , z2 , z3 , z5, z2 , z4. Для этого воспользуемся формулой:
 ,
,
где
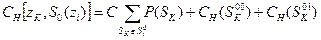 ;
;
Таблица 18
| S1 | ZI | P(S1) | ||||
| Z5 | Z1 | Z2 | Z3 | Z4 | ||
| S1 0 0 0 1 0 0,2 S2 0 1 0 1 0 0,05 S3 0 1 1 1 1 0,06 S4 1 1 1 0 0 0,24 S5 1 1 1 1 0 0,15 S6 1 1 1 1 1 0,3 | ||||||
 ,
,
где ∑ Р(SK) и ∑ Р(SJ) суммы вероятностей Р(S) диагностируемого объекта, которые различаются контролем параметров zK и zJ в подмножествах  и
и 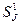 соответственно.
соответственно.
Вычислим значения стоимостей нижних границ при контроле параметров z5 , z1 , z3 . Контроль параметров z1 позволяет различать состояния S1 , S2 , S5 , следовательно,
∑ P(SK) = Р(S1) + Р(S2) + Р(S2) = 0,2 + 0,05 + 0,06 = 0,31
|
|
|
Также при контроле параметра zI выделяется из подмножества S0(zК) только одно состояние S001 , тогда CН (S001) = 0, а значения CН (S101) вычисляется аналогичным способом, как и CН (S01):
К
CН (S101) = С ∑Р*V = С [Р (S2) + Р (S5)] = C (0,05 + 0,06) = 0,11C
При контроле параметра z3 различаются состояния S3 , S4 , S6, следовательно:
∑ P(SJ) = Р(S3) + Р(S4) + Р(S6) = 0,24 + 0,15 + 0,3 = 0,69
Кроме того, при отрицательном исходе из множеств S1(z5) выделяется только одно состояние, а при положительном – два, следовательно:
CН (S10J) = CН (S103) = 0
К
CН (S11J) = С ∑ Р*V = С [Р (S4) + Р (S6)] = C (0,15 + 0,3) = 0,45C
V
Тогда значение стоимости нижней границы при контроле параметров z5 , z1 , z3 будет равно
CН (z5 , z1 , z3,) = С(1 + 0,31 + 0,11 + 0,69 + 0,45) = 2,56С
При контроле других последовательностей параметров вычисления осуществляются аналогично. Приведем результаты этих вычислений:
CН (z5 , z1 , z4,) = 2,5С
CН (z5 , z2 , z4,) = 2,64С
CН (z5 , z2 , z3,) = 2,7С
Анализ результатов вычислений стоимостей нижних границ показывает, что минимальной стоимостью будет обладать последовательность параметров z5 , z1 , z4.
Таблица19
| SI | ZI | P(SI) | ||||
| Z5 | Z1 | Z4 | Z2 | Z3 | ||
SI 0 0 0 0 1 0,2 } S00 (z5, z1) SI 0 1 0 0 1 0,05 SI 0 1 1 1 1 0,24 SI 1 1 0 1 0 0,15 SI 1 1 0 1 1 0,06 SI 1 1 1 1 1 0,3 } S11 (z5, z4)
| ||||||
Преобразуем таблицу неисправностей в соответствии с результатами контроля последовательности параметров z5 , z1 , z4 (табл. 19).
Из таблицы видно, что при отрицательном исходе контроля параметров z5 и z1 выделяется состояние S1, а при отрицательном исходе контроля z5 и положительном z1 необходимо следующим контролировать параметр z2 (контроль параметра z3 не позволяет разделить подмножество S01 на более мелкие).
При положительном исходе контроля параметров z5 и z4 выделяется состояние S6, а при отрицательном исходе контроля параметров z5 и отрицательном z4 необходимо контролировать параметр z3. Поскольку других вариантов нет, на этом заканчивается построение алгоритма поиска неисправностей, обладающего минимальной средней стоимостью (Рис. 13).
Таким образом, последовательность контролируемых параметров z5 , z1, z4, z2 , z3 дает среднюю стоимость ССР = 2,5С.
 |
|
|
|
 начало
начало
 | |||
 | |||
|





 Z1 Z2 Z3 Z4 Z5
Z1 Z2 Z3 Z4 Z5
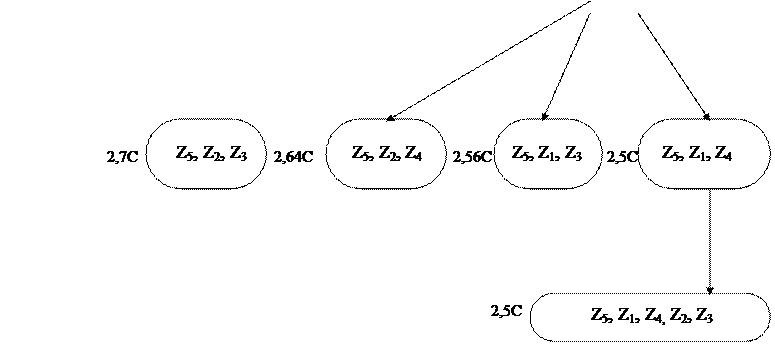
Рис. 13 Схема алгоритма поиска неисправностей, построенного методом ветвей и границ
3.8 Метод диагностики на основе «белого шума»
Интегральный метод диагностики на основе «белого шума» позволяет определить отклик диагностируемой системы во время ее нормальной работы, то есть без отключения. Известно, что для «белого шума» автокорреляционная функция равна нулю при всех значениях τ, кроме точки τ = 0, где случайная функция умножается сама на себя:
 (51)
(51)
где Uш1 (t) – напряжение белого шума на входе ОД.
Связь между напряжениями входа и выхода диагностируемой системы через отклик h(t) определяется уравнением
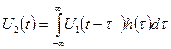 (52)
(52)
Известно, что взаимная корреляционная функция входа и выхода системы выражается через автокорреляционную функцию
 (53)
(53)
После перемены аргументов τ и t получим
 (54)
(54)
Если на вход системы подать стимулирующее напряжение
δ(t) = U1(t) (55)
то уравнение (52) упрощается и напряжение на выходе системы становится равным отклику диагностируемой аппаратуры:
U2 (t) = h (t) (56)
Из сравнения выражений (52), (53) и (56) следует, что при подаче на вход ОД сигнала в виде «белого шума», корреляционная функция которого является дельта-функцией R11(t) = δ(t), взаимно корреляционная функция входа и выхода будет равна отклику системы:
R12(t) = h (t) (57)
 U1(t) UW2 (t)+U2(t)
U1(t) UW2 (t)+U2(t)
 |
R12(t)=h(t)
Генератор Коррелятор
«белого шума»
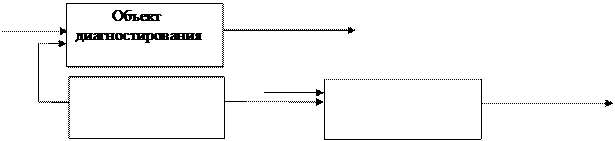
Рис. 14 Схема для определения отклика диагностируемой системы.
Равенство (7) позволяет синтезировать схему (рис.1), которая с помощью коррелятора может определить отклик системы по напряжению «белого шума» на ее входе.
Если на вход подать напряжение Uс1 (t), то на ее выходе получим суммарный сигнал
U2 (t) = Uш2 (t) + Uс2 (t) (58)
где Uс2 (t) – напряжение, которое появляется на выходе контролируемой аппаратуры после прохождения через нее сигнала Uс1 (t), Uш2 (t) – напряжение на выходе аппаратуры.
|
|
|
|
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 475; Нарушение авторских прав?; Мы поможем в написании вашей работы!