Раскрытие неопределенностей

ПРИМЕНЕНИЕ ПРОИЗВОДНЫХ В ИССЛЕДОВАНИИ ФУНКЦИЙ

Правило Лопиталя

Отношение двух функций 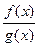при x 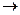a есть неопределенность вида 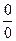, если

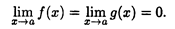
Раскрыть эту неопределенность означает вычислить предел 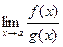, если он существует.

ТЕОРЕМА (теорема Лопиталя). Пусть функции f(x) и g(х) определены и дифференцируемы в некоторой окрестнос­ти точки а за исключением, быть может, самой точки a. Кроме того, пусть 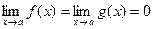, причем g'(х) ≠ 0 в указанной окрестности точки а. Тогда если существует предел отношения 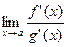(конечный или бесконечный), то существует и предел 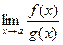, причем справедлива формула

=

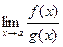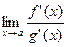
Эту теорему обычно называют правилом Лопиталя.

Замечание 1. Правило Лопиталя можно применять повторно, если f'(x) и g'(х) удовлетворяют тем же требо­ваниям, что и исходные функции f(x) и g(х).

Замечание 2. Теорема остается верной и в случае, когда x→∞ (х ± ).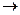

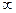Неопределенности вида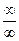

Отношение двух функций 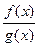при х 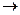а называется неопределенностью вида 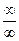, ес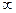ли (-или +).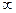

Правило Лопиталя остается справед­ливым при замене условия 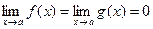на условие .

Пример: Найти lim x/e^x

x→∞

Решение: lim x/e^x = [∞/∞] = lim x^'/(e^x)' = lim 1/e^x = 0

x→∞ x→∞ x→∞

Другие виды неопределенностей

Неопределенности вида 0 ∙ 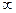и 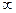— 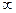можно свести к неопределенностям вида 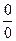и 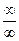. Покажем это на примерах.

Пример: Найти предел 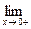x ln x.

Решение. Здесь неопределенность вида 0 ∙ 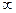. Преобразуем функцию под знаком предела: х ln х = 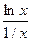и теперь уже имеем неопределенность вида 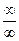при х 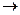0 +. Теперь, применяя правило Лопиталя, получаем

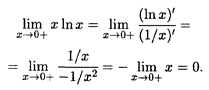
Пример: Найти (cosec x — ctg x).

Решение. Это неопределенность вида 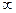— 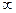. Преобразуя функцию под знаком предела, получаем

(4)

Неопределенность (4) вида 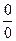при х 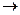0. Согласно правилу Ло­питаля

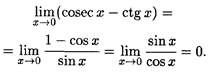
Рассмотрим неопределенности вида 0⁰, 1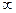, 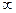⁰, возникаю­щие при вычислении пределов функций у = и(х)^v(x). Неопреде­ленности этого вида сводятся к неопределенности вида 0 ∙ 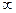с помощью тождественного преоб­разования

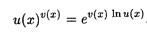(5)

Пример: Найти предел .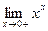

Решение. Это предел вида 0⁰; используя формулу (5), имеем с учетом решения первого примера

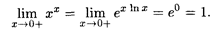
Пример: Найти предел

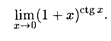
Решение. Это предел вида 1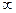. Найдем предел функции у = ctg x ln(1 + x) при x 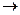0. В соответствии с представлением (5) имеем следующую цепочку равенств:

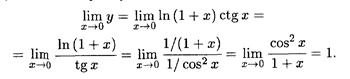
Следовательно, искомый предел равен

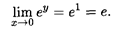
Разложение функций по формуле Маклорена

Функцию f (x), имеющую (n + 1) производных в точке х = 0, можно представить по формуле Маклорена вместе с остаточным членом:

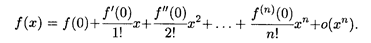(6)

Пример: f (x) = е^x.

Решение. Поскольку (e^x)^{( n )} = e^х, f⁽ⁿ⁾ (0) = е ⁰ = 1 для любого п, формула Маклорена (6) имеет вид

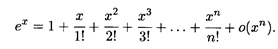(7)

Формула (7) используется для вычисления числа е с лю­бой необходимой точностью. Отсюда при х = 1 получаем при­ближенное значение числа е ≈ 2,7182818....

Формула (6) представляет собой асимптотичес­кую формулу (или оценку) для функции e^х при x 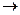0. Аналогичные раз­ложения можно получить с использованием формулы (6) и для других функций. Асимптотические формулы эффективно применяются при вычислении пределов функций.

Дата добавления: 2014-01-05