Упражнения

Если же, то для «свободных» неизвестных мы возьмем произвольные числовые значения, после чего, двигаясь по системе (9) снизу вверх, мы найдем для неизвестных вполне определенные значения. Так как значения для свободных неизвестных можно выбрать бесконечным числом различных способов, то система (9) и, следовательно, система (6) будут совместными, неопределенными.

Подводя итог, можно сказать следующее: метод Гаусса применим к любой системе линейных уравнений. При этом система будет несовместной, если в процессе преобразований мы получим уравнение, в котором коэффициенты при всех неизвестных равны нулю, а свободный член отличен от нуля; если же мы такого уравнения не встретим, то система будет совместной. Совместная система уравнений будет определенной, если она приводится к треугольному виду (9), и неопределенной, если приводится к трапецеидальному виду (10).

Применим все вышеизложенное к системам линейных однородных уравнений. Если в системе линейных однородных уравнений число уравнений меньше числа неизвестных, то эта система обладает, помимо нулевого решения, также и ненулевыми решениями, т.е. решениями, в которых значения некоторых (или даже всех) неизвестных отличны от нуля. Таких решений будет бесконечно много.

При практическом решении системы линейных уравнений методом Гаусса следует выписать матрицу из коэффициентов системы, присоединить к ней столбец из свободных членов, для удобства отделенный вертикальной чертой, и все преобразования выполнять над строками этой «расширенной» матрицы.

Пример 8. Решить систему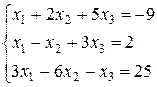

Решение:

Произведем вышеописанные преобразования с расширенной матрицей системы.

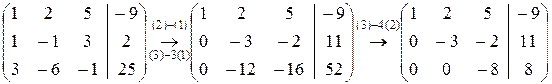
Таким образом, мы приходим к следующей системе уравнений

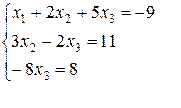
Эта система обладает единственным решением: 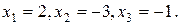Значит, она является определенной.

Пример 9. Решить систему

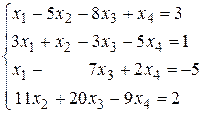
Решение.

1) Из третьей строки вычесть первую, далее третью строку умножить на 3 и вычесть из второй.

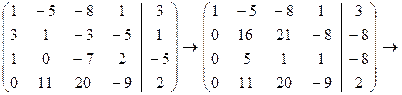
2) Поменять местами второй и третий столбцы, а потом вторую и третью строки.

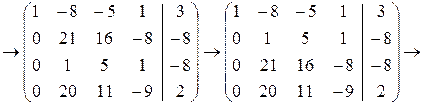
3) Из третьей строки вычесть вторую, умноженную на 21, затем из четвертой строки вычесть вторую, умноженную на 20. Далее из четвертой строки вычесть третью.

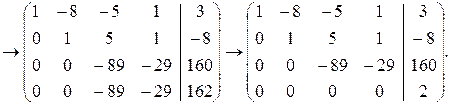
Мы пришли к системе, содержащей уравнение 0=2. Исходная система будет, следовательно, несовместной.

Пример 10. Решить систему

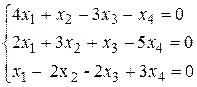
Решение.

Эта система однородных уравнений, причем число уравнений меньше числа неизвестных; она должна быть поэтому неопределенной. Так как все свободные члены равны нулю, то мы будем подвергать преобразованиям лишь матрицу из коэффициентов системы:

1) Поменяем местами первую и третью строки.

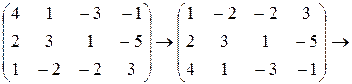
2) Из второй строки вычтем первую, умноженную на 2, из третьей строки вычтем первую, умноженную на 4.

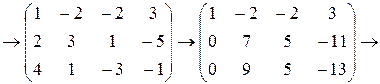
3) Поменять местами второй и третьей столбец. Из третьей строки вычесть вторую.

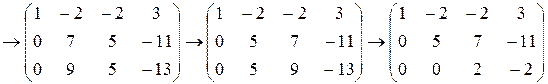
Мы пришли к системе уравнений: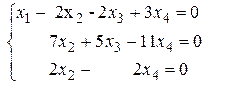

В качестве свободного неизвестного можно принять любое из неизвестных 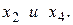Пусть 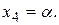Тогда из первого уравнения следует 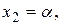после чего из второго уравнения получаем 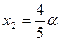, а из третьего уравнения 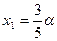. Таким образом, общий вид решений заданной системы уравнений:.

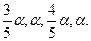1. Решить систему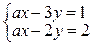

где а – некоторый числовой параметр. Указать, при каких значениях а система: а) имеет единственное решение; б) не имеет решений; в) имеет бесчисленное множество решений.

Ответ: а) При 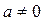система имеет единственное решение (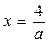;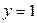); б) при 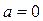система не имеет решений; в) бесчисленного количества решений система ни при каких значениях а иметь не может.

2. Методом Гаусса решить систему

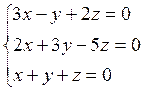
Ответ: система имеет лишь тривиальное решение (; ; ).

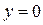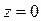3. Показать, что переопределенная система

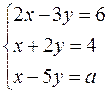
может иметь решение. При каком значении параметра а это будет иметь место?

Ответ: при 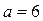система имеет единственное решение (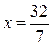; 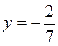). При 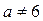система не имеет решений.

4. Решить недоопределенную систему

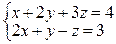
Ответ: система имеет бесчисленное множество решений

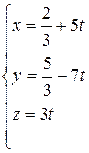(t – свободный параметр)

5. Решить недоопределенную систему

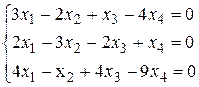
Ответ: система имеет бесчисленное множество решений

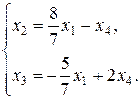(x₁,x₂ – свободные параметры)

6. Методом Гаусса решить систему: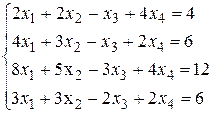

Ответ: (1,1,-1,-1).

Дата добавления: 2014-01-05