
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Способи обертання
|
|
|
|
Зміна положення предмета щодо незмінних площин проекцій може здійснюватись обертанням його навколо деяких осей, які називаються осями обертання. Кожна точка предмета при цьому переміщується по колу (колу обертання), площина якого перпендикулярна до осі обертання, його радіус дорівнює відстані від точки, що обертається, до осі обертання, тобто перпендикуляру, проведеному від точки до осі обертання, центр кола знаходиться в основі цього перпендикуляра.
Якщо вісь обертання перпендикулярна до якоїсь площини проекцій, то маємо спосіб обертання навколо проекціювальної осі. У цьому разі кола обертання проекціюються без спотворення на площину проекцій, до якої вісь обертання перпендикулярна, а на другу – у відрізки прямих, що перпендикулярні до проекції осі обертання (рис. 6.9).
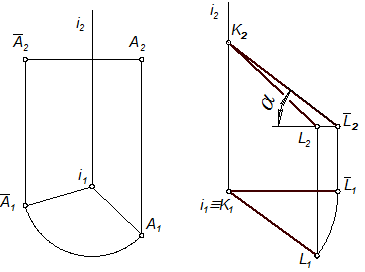 За допомогою цього способу зручно визначати дійсну довжину відрізка прямої, наприклад, довжину бічних ребер піраміди для побудови розгортки її поверхні. На рис. 6.10 показано визначення дійсної довжини відрізка KL (K1L1, K2L2). Через точку K(K1, K2) проведена горизонтально проекціювальна вісь i(i1, i2) і точка L(L1, L2) повернута навколо осі і так, що відрізок KL став паралельним площині П2. Точка L1 перемістилась у положення
За допомогою цього способу зручно визначати дійсну довжину відрізка прямої, наприклад, довжину бічних ребер піраміди для побудови розгортки її поверхні. На рис. 6.10 показано визначення дійсної довжини відрізка KL (K1L1, K2L2). Через точку K(K1, K2) проведена горизонтально проекціювальна вісь i(i1, i2) і точка L(L1, L2) повернута навколо осі і так, що відрізок KL став паралельним площині П2. Точка L1 перемістилась у положення 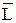 1, а фронтальна її проекція L2 перемістилась у положення
1, а фронтальна її проекція L2 перемістилась у положення 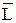 2 (L2
2 (L2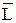 2 ^ і2). Відрізок K2
2 ^ і2). Відрізок K2 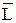 2 становить дійсну довжину відрізка KL, а кут a - це дійсна величина кута нахилу відрізка KL до площини проекцій П1.
2 становить дійсну довжину відрізка KL, а кут a - це дійсна величина кута нахилу відрізка KL до площини проекцій П1.
Способом обертання Рис. 6.9 Рис. 6.10
навколо проекціювальних
осей можна розв’язувати такі самі задачі як і способом заміни площин проекцій. Зокрема, цим способом доцільно користуватись для визначення дійсних довжин ребер пірамід та твірних конусів для побудови їхніх розгорток і т. ін. Але трудомісткість та складність розв’язування багатьох задач цим способом значно вища, ніж іншими способами. Тому більш детально застосування цього способу тут не розглядаємо.
|
|
|
Обертання фігур навколо проекціювальної осі може здійснюватись без вказування осі. Такий спосіб називається способом плоско паралельного переміщення. Він ґрунтується на тому, що проекція предмета на площину проекцій, до якої вісь обертання перпендикулярна, залишається конгруентною вихідній проекції незалежно від того, як би не рухався предмет. Змінюється лише положення проекції.
Спосіб плоско паралельного переміщення полягає у тому, що предмет пересувається так, що кожна його точка рухається у одній площині, паралельній якій-небудь площині проекцій. Тоді на іншу площину проекцій ці площини проекціюються у прямі, що паралельні осі проекцій. Траєкторія руху кожної точки може бути будь-якою лінією, розташованою у площині рівня, і тому на відповідній площині проекцій не зображується. Спосіб плоско паралельного переміщення може застосовуватись для розв’язування тих самих задач, що і способом заміни площин проекцій, але деякі задачі розв’язуються цим способом складніше, ніж заміною площин проекцій. Перевагою цього способу є те, що побудови можна виконувати на вільному місці креслення.
Далі розглянемо приклади застосування способу для розв’язування чотирьох основних задач.
Задача 1. Перетворити креслення прямої AB(A1B1, A2B2) загального положення так, щоб вона стала прямою рівня (рис. 6.11).
 Перемістимо пряму AB так, щоб вона стала, наприклад, фронтальною. У цьому разі кожна точка прямої AB пересуватиметься у своїй площині, паралельній горизонтальній площині проекцій. Горизонтальна проекція A1B1 відрізка прямої AB не змінюватиме своєї довжини, оскільки не змінюється кут нахилу прямої до горизонтальної площини проекцій. Тому горизонтальну проекцію прямої перенесемо на нове місце у положення
Перемістимо пряму AB так, щоб вона стала, наприклад, фронтальною. У цьому разі кожна точка прямої AB пересуватиметься у своїй площині, паралельній горизонтальній площині проекцій. Горизонтальна проекція A1B1 відрізка прямої AB не змінюватиме своєї довжини, оскільки не змінюється кут нахилу прямої до горизонтальної площини проекцій. Тому горизонтальну проекцію прямої перенесемо на нове місце у положення 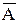 1
1 1 неподалік від вихідної проекції A1B1, розташувавши її перпендикулярно до лінії зв’язку A1A2. Кожна із точок A і B пересуватиметься у Рис. 6.11
1 неподалік від вихідної проекції A1B1, розташувавши її перпендикулярно до лінії зв’язку A1A2. Кожна із точок A і B пересуватиметься у Рис. 6.11
|
|
|
своїй горизонтальній
площині, яка зображується на фронтальній площині проекцій горизонтальною прямою, що проходить відповідно через проекцію A2 чи B2 точок A і B.
Вертикальні лінії зв’язку 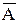 1
1 2 і
2 і 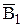
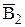 у перетині з цими горизонтальними лініями визначають нові фронтальні проекції
у перетині з цими горизонтальними лініями визначають нові фронтальні проекції 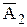 і
і 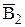 точок А і В. Сполучивши точки
точок А і В. Сполучивши точки 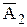 і
і 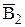 відрізком прямої, маємо нову фронтальну проекцію
відрізком прямої, маємо нову фронтальну проекцію 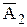
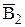 відрізка АВ.
відрізка АВ. 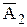
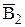 - це неспотворена проекція відрізка АВ (
- це неспотворена проекція відрізка АВ (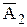
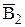 = АВ). Кут a - це кут нахилу прямої АВ до площини проекцій П1.
= АВ). Кут a - це кут нахилу прямої АВ до площини проекцій П1.
Раніше говорилося, що плоско паралельне переміщення - це обертання навколо проекціювальних осей, які не вказуються на кресленні. Але їхнє положення легко можна встановити. Так, наприклад, на рис. 6.11 можна сполучити точки А1 і  та В1 і
та В1 і 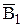 відрізками А1
відрізками А1 і В1
і В1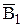 прямих. Провівши серединні перпендикуляри до відрізків А1
прямих. Провівши серединні перпендикуляри до відрізків А1 і В1
і В1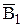 , у їхньому перетині матимемо горизонтальну проекцію осі i1, навколо якої відрізок АВ(А1В1, А2В2) повернуто у положення
, у їхньому перетині матимемо горизонтальну проекцію осі i1, навколо якої відрізок АВ(А1В1, А2В2) повернуто у положення 
 (
(
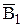 ,
, 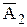
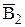 ). Але у побудові проекцій
). Але у побудові проекцій 
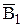 та
та 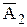
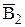 ця вісь не використовувалася, тому вона і не зображена на рис. 6.11. І у подальших прикладах ми не говоритимемо про ці осі.
ця вісь не використовувалася, тому вона і не зображена на рис. 6.11. І у подальших прикладах ми не говоритимемо про ці осі.
Задача 2. Перетворити креслення прямої АВ(А1В1, А2В2) загального положення так, щоб вона стала проекціювальною.
Оскільки при переміщенні предмета щодо якоїсь площини проекцій кожна точка його пересувається у своїй площині, паралельній відповідній площині проекцій, то перемістити пряму загального положення так, щоб вона відразу стала перпендикулярною до якоїсь площини проекцій неможливо. Тому спочатку пряму слід перемістити щодо якоїсь площини проекцій у положення відповідної лінії рівня, а потім переміщенням щодо іншої площини проекцій пряму можна перевести у положення перпендикуляра до відповідної площини проекцій.
Наприклад, пряму АВ перетворюємо у фронтальну пряму переміщенням її щодо площини П1, як це зроблено на рис. 6.11. Потім другим переміщенням щодо площини П2 пряму розташовуємо перпендикулярно до площини П1, тобто пряму перетворюємо на вертикальну. Отже, продовжуючи побудови задачі 1 на рис. 6.11, проекцію 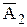
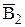 прямої АВ пересуваємо у положення
прямої АВ пересуваємо у положення 
 . Слід зауважити, що
. Слід зауважити, що 
 =
= 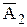
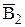 ,
, 
 ||А1А2. При такому переміщенні всі точки прямої
||А1А2. При такому переміщенні всі точки прямої 
 (
(
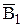 ,
, 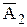
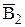 ) пересуваються у одній фронтальній площині. Коли ж пряма стає перпендикулярною до площини П1 горизонтальні проекції всіх її точок збігаються у одній точці
) пересуваються у одній фронтальній площині. Коли ж пряма стає перпендикулярною до площини П1 горизонтальні проекції всіх її точок збігаються у одній точці  =
=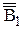 .
.
|
|
|
На основі другої основної задачі можна визначати відстані від точки до прямої, між двома прямими (паралельними чи мимобіжними), двогранний кут між двома площинами, якщо відома їхня лінія перетину.
Так на рис. 6.11 показано визначення натуральної величини відстані від точки М(М1, М2) до прямої АВ. Слідом за перетвореннями прямої разом із нею пересуваємо і точку М спочатку у положення  (
(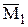 ,
,  ), а потім у положення
), а потім у положення 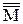 (
( ,
, 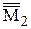 ). Необхідно зазначити, що точка М пересувається у нове положення разом із прямою як єдине ціле, тобто без порушення їхнього взаємного розташування. Так, проекція
). Необхідно зазначити, що точка М пересувається у нове положення разом із прямою як єдине ціле, тобто без порушення їхнього взаємного розташування. Так, проекція 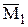 точки М знаходиться у перетині двох дуг кіл радіусами, які становлять відстані від точки М1 до точок А1 і В1 (
точки М знаходиться у перетині двох дуг кіл радіусами, які становлять відстані від точки М1 до точок А1 і В1 (
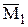 = А1М1,
= А1М1, 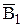
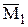 = В1М1). Проекція
= В1М1). Проекція  точки М знаходиться у перетині вертикальної лінії зв’язку
точки М знаходиться у перетині вертикальної лінії зв’язку 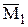
 і горизонтальної прямої М2
і горизонтальної прямої М2  - фронтальної проекції площини переміщення точки М.
- фронтальної проекції площини переміщення точки М.
При другому переміщенні точки М її проекція 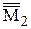 знайдена у перетині дуг двох кіл радіусами, що становлять відстані від точки
знайдена у перетині дуг двох кіл радіусами, що становлять відстані від точки  до точок
до точок 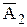 і
і 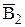 (
(
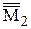 =
=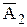
 ,
, 
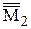 =
=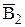
 ). Тут точка
). Тут точка  пересувається у фронтальній площині і нова її проекція
пересувається у фронтальній площині і нова її проекція  знаходиться у перетині вертикальної лінії зв’язку
знаходиться у перетині вертикальної лінії зв’язку 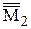
 з горизонтальною лінією
з горизонтальною лінією 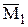
 . Відрізок
. Відрізок 
 становить дійсну величину відстані від точки М до прямої АВ.
становить дійсну величину відстані від точки М до прямої АВ.
Задача 3. Перетворити креслення так, щоб площина Г(D АВС) стала проекціювальною (рис. 6.12).
Площина Г при переміщенні стане перпендикулярною до площини проекцій, якщо якась пряма, що розташована у площині Г, стане перпендикулярною до цієї площини проекцій. Зважаючи на те, що при переміщенні фігури кожна її точка рухається у своїй площині рівня, то такою прямою площини Г може бути тільки лінія рівня.
 Отже у DАВС(DА1В1С1, DА2В2С2) проводимо якусь лінію рівня, наприклад, горизонталь h(h1, h2) через вершину В(В1, В2). Переміщуємо горизонтальну проекцію В111 горизонталі h у положення
Отже у DАВС(DА1В1С1, DА2В2С2) проводимо якусь лінію рівня, наприклад, горизонталь h(h1, h2) через вершину В(В1, В2). Переміщуємо горизонтальну проекцію В111 горизонталі h у положення 
 , розташувавши її на вільному місці неподалік від вихідної проекції DА1В1С1.
, розташувавши її на вільному місці неподалік від вихідної проекції DА1В1С1.
|
|
|
На відрізку 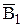
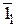 будуємо трикутник
будуємо трикутник 
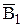
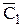 , конгруентний DА1В1С1. Вершина
, конгруентний DА1В1С1. Вершина  знаходиться як точка перетину дуг двох кіл, радіуси яких становлять відстані від точки А1 до точок відповідно В1 і 11. Аналогічно побудована і вершина
знаходиться як точка перетину дуг двох кіл, радіуси яких становлять відстані від точки А1 до точок відповідно В1 і 11. Аналогічно побудована і вершина 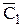 . D
. D
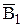
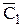 - це нова горизонтальна проекція переміщеного трикутника АВС. Фронтальну проекцію D
- це нова горизонтальна проекція переміщеного трикутника АВС. Фронтальну проекцію D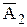
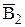
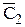 переміщеного трикутника АВС знаходимо за допомогою вертикальних ліній зв’язку та горизонтальних ліній, проведених через вершини А2, В2, С2. Наприклад, вершина
переміщеного трикутника АВС знаходимо за допомогою вертикальних ліній зв’язку та горизонтальних ліній, проведених через вершини А2, В2, С2. Наприклад, вершина 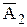 Рис. 6.12
Рис. 6.12
побудована як точка перетину:
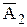 =
= 
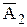
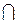

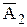 . Аналогічно побудовані вершини
. Аналогічно побудовані вершини 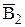 і
і 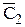 . Як бачимо, вершини
. Як бачимо, вершини 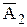 ,
, 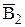 ,
,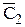 розташувались на одній прямій, бо площина Г(DАВС) стала фронтально проекціювальною. Кут між проекцією
розташувались на одній прямій, бо площина Г(DАВС) стала фронтально проекціювальною. Кут між проекцією 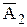
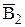
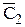 і горизонтальною лінією
і горизонтальною лінією 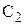
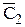 - це кут нахилу площини Г до горизонтальної площини проекцій.
- це кут нахилу площини Г до горизонтальної площини проекцій.
На основі 3-ї основної задачі можна визначити кути нахилу площини загального положення до площин проекцій, а також відстань від точки до площини, від прямої до площини та між двома паралельними площинами.
На рис. 6.12 показано визначення відстані від точки К(К1, К2) до площини Г(DАВС). Для цього разом з переміщенням трикутника АВС в положення 

 перемістили і точку К так, щоб не порушилось розташування точки К щодо трикутника АВС. Так, точка
перемістили і точку К так, щоб не порушилось розташування точки К щодо трикутника АВС. Так, точка  знайдена як точка перетину дуг двох кіл:
знайдена як точка перетину дуг двох кіл: 
 = К1А1,
= К1А1, 
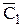 = К1С1. Фронтальна проекція
= К1С1. Фронтальна проекція  точки К знайдена у перетині лінії зв’язку
точки К знайдена у перетині лінії зв’язку 
 та горизонтальної лінії
та горизонтальної лінії 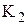
 . Перпендикуляр, проведений від точки
. Перпендикуляр, проведений від точки  до проекції
до проекції 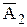
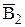
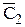 трикутника АВС, становить дійсну величину відстані від точки К до площини Г(DАВС).
трикутника АВС, становить дійсну величину відстані від точки К до площини Г(DАВС).
Задача 4. Перетворити креслення так, щоб площина L(DDEF) стала площиною рівня (рис. 6.13).
Площину загального положення неможливо перевести одним переміщенням у положення площини рівня. Це зумовлено особливостями способу плоско паралельного переміщення. Тому площину L спочатку слід перетворити на проекціювальну, перемістивши її щодо однієї із площин проекцій, як це зроблено у задачі 3, а потім другим переміщенням щодо другої площини проекцій привести її у положення площини рівня.
Проведемо у площині L, наприклад, фронталь f(f1, f2) і перемістимо
DDEF(DD1E1F1, DD2E2F2) паралельно площині проекцій П2 так, щоб фронталь f стала вертикальною: 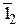
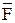 2|| Е2Е1,
2|| Е2Е1, 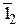
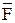 2 =12F2. На відрізку
2 =12F2. На відрізку 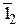
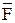 2 фронталі будуємо D
2 фронталі будуємо D
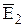
 , конгруентний DD2E2F2 :
, конгруентний DD2E2F2 : 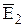
 = E2F2,
= E2F2, 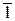 2
2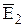 = 12Е2;
= 12Е2;

 = D2F2,
= D2F2, 
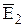 = D2E2. За такого положення трикутника
= D2E2. За такого положення трикутника 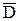
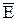
 на площину проекцій П1 він спроекціюється у відрізок
на площину проекцій П1 він спроекціюється у відрізок 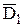
 прямої лінії. Точки
прямої лінії. Точки 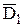 ,
,  ,
,  знаходимо як точки перетину відповідних вертикальних ліній зв’язку з горизонтальними прямими, по яких пересуваються горизонтальні проекції вершин D, E, F. Як бачимо до складу задачі 4 входить як її перша складова частина задача 3.
знаходимо як точки перетину відповідних вертикальних ліній зв’язку з горизонтальними прямими, по яких пересуваються горизонтальні проекції вершин D, E, F. Як бачимо до складу задачі 4 входить як її перша складова частина задача 3.
Далі проекцію 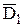

 трикутника переміщуємо паралельно площині проекцій П1 у положення
трикутника переміщуємо паралельно площині проекцій П1 у положення 
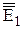
 . Для цього на вільному місці проводимо відрізок прямої, перпендикулярної до лінії
. Для цього на вільному місці проводимо відрізок прямої, перпендикулярної до лінії 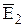
 і наносимо на нього точки
і наносимо на нього точки  ,
,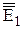 ,
, так, щоб
так, щоб 
 =
= 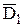
 ,
, 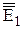
 =
= 
 . Проекції
. Проекції 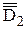 ,
,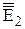 ,
, 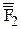 вершин трикутника DEF знаходимо як точки перетину ліній зв’язку
вершин трикутника DEF знаходимо як точки перетину ліній зв’язку 
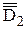 ,
, 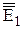
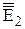 ,
, 
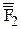 з горизонтальними прямими, по котрих пересуваються фронтальні проекції трикутника DEF. Сполучивши точки
з горизонтальними прямими, по котрих пересуваються фронтальні проекції трикутника DEF. Сполучивши точки 
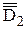 ,
,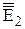 ,
, 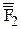 відрізками прямих, маємо трикутник
відрізками прямих, маємо трикутник 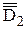
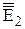
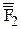 , який є неспотвореною проекцією вихідного трикутника DEF. Таким чином, на основі задачі 4 можна знайти неспотворену Рис. 6.13
, який є неспотвореною проекцією вихідного трикутника DEF. Таким чином, на основі задачі 4 можна знайти неспотворену Рис. 6.13
проекцію будь-якої
плоскої фігури, кути між прямими, що належать цій фігурі, центри вписаного в трикутник та описаного навколо нього кола і т. ін.
|
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 2848; Нарушение авторских прав?; Мы поможем в написании вашей работы!