Свойства проекции вектора на ось

Проекция вектора на ось не изменится от параллельного переноса вектора.

Аддитивность проекции. Проекция суммы векторов на некоторую ось равна сумме проекций данных векторов на эту ось.

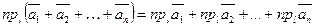. (1.1)

. Однородность проекции. Скалярный множитель можно вынести за знак проекции вектора на ось,

. (1.2)

Определение 1.4. Углом между вектором и осью называется угол между вектором и положительным направлением оси, отсчитываемый в направлении от оси против движения часовой стрелки (рис. 1.4).

. Проекция вектора на ось равна произведению модуля этого вектора на косинус угла 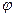между вектором и осью, (рис. 1.3),

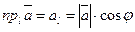(1.2)

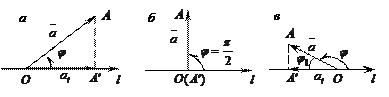Рис. 1.4

Доказательство. Проведем доказательство для случая, когда угол 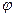между вектором и осью является острым.

Пусть (рис. 1.4, а). Из Δ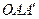следует:

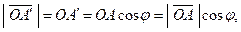или,

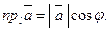
Не составляет большого проведение доказательства для стальных случаев.

Задача 1.1. Дано: , , , .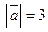

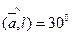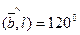Найти _.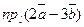

Решение. Воспользуемся определением понятия и свойствами проекций.

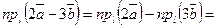
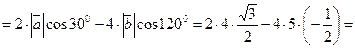
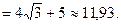
2. Декартова прямоугольная система
координат в пространстве

Дата добавления: 2014-01-05