Метод исключения

Численное решение:

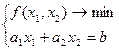
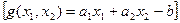
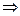точка min должна лежать на прямой.

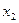
g(x)

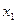
В каждый момент линия уровня будет касаться прямой 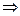эта точка и является точкой

условного локального min. Если в окрестности заданной точки, удовлетворяющей

всем значениям равенства, значение функции больше, чем в точке, то эта точка – есть точка условного локального min.

Пример:

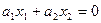
(a,x)=0

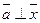
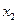
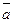
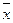
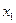
Если (a₁x)=b

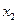
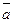
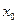
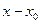
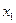
Допустим,

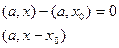
Прямая будет проходить через некоторую точку удовлетворяющую условию и

Для n переменных , Ax=b

Рассмотрим i-ое ограничение:

,

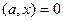
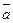- задан x - все вектора, лежащие . Они и составляют гиперплоскость.

При добавлении еще одного условия, уменьшаются размерности. В конечном итоге получится пространство n-m.

Для двух переменных возможно 2 случая:

1.

2.

В случае 2 это не точка минимума, а седловая точка.

Рассмотрим точку 3-х переменных:

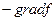плоскость

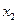
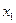
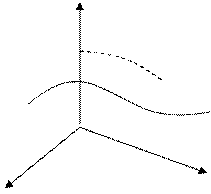
Ограничение – плоскость, следовательно, все допустимые точки на плоскости. Если угол grad не равен 90 градусам следовательно можно двигаться дальше. На плоскости существует направление, которое будет составлять острый угол с – grad, и двигаясь в этом направлении можно уменьшить значение f. Если -grad f перпендикулярен плоскости эта точка может быть точкой минимума.

Пусть существует 2 ограничения:

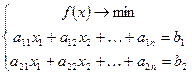
Рассмотрим опять случай 3-х переменных:

Точка минимума должна принадлежать пересечению плоскостей.

Необходимое условие – вектор антиградиента должен составлять угол 90 градусов с прямой пересечения плоскостей.

Для п -мерного случая имеется п переменных следовательно рассматривая каждое ограничение, получаем п-1 гиперплоскость следовательно рассмотрев т ограничений получим п-т гиперплоскость (т<п).

все ограничения независимы

Если вектор grad (п -мерный) будет ортогонален п-т – пространству.

Допустим имеется п-1 пространство, п -мерный вектор может принадлежать ему или нет. Пусть вектор не принадлежит данному подпространству следовательно его можно разложить на 2 вектора – один который принадлежит подпространству, и второй который ортогонален данному. Ортогональное дополнение – вектора, которые ортогональны данному подпространству.

В 3D – пространстве, если подпространство равно 1 следовательно ортогональное дополнение равно 2.

В п-т -мерном подпространстве ортогональное дополнение имеет размерность т.

Необходимое условие: Если мы находим точку, где вектор градиента принадлежит ортогональному дополнению к пространству, заданному ограничениями – равенствами, то эта точка может быть точкой локального минимума.

Пусть есть 2 плоскости. Если записать систему ограничений равенств следующим образом:

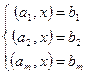
где

Т.о. вектора 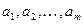порождают ортогональное дополнение. Существующие могут быть выбраны в качестве базиса ортогонального дополнения следовательно градиент принадлежит ортогональному дополнению:

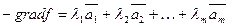
т.е. линейная комбинация базисных векторов.

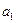
- множители Лагранжа.

Рассмотрим матрицу , в ней - столбцы.

это условие может быть использовано для численного решения задачи оптимизации с ограничивающими уравнениями.

Пример:

Если найдем такие вектора х и , для которых эти условия выполняются то точка может быть точкой локального минимума.

Рассмотрим случай когда система ограничений – равенств нелинейная:

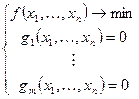
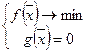
Если функции дифференцируемы, то в окрестности точки минимума они будут вести себя как линейные.

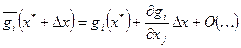следовательно в окрестности точки локального минимума эта зависимость линейная следовательно получается система вида: , где

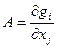
следовательно необходимое условие локального минимума:

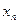
n-m

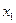
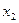
- множители Лагранжа.

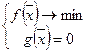
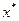- точка может быть искомой в задаче

- множители Лагранжа.

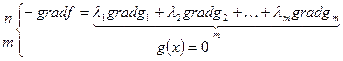
Обозначения для скалярного произведения ;

;

Необходимое условие точки локального минимума исходное задание с ограничениями представляет собой необходимое условие точки локального экстремума для функции Лагранжа.

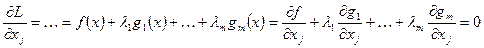
Дата добавления: 2014-01-05