
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Решение ТЗ в сетевой постановке методом буферного запаса
|
|
|
|
Лекция №5.
Построение ММ. При этом методе решения ТЗ узлы ТС классифицируются следующим образом:
1. Узел i называется источником, если существуют только выходящие из него дуги.
2. Узел i называется стоком, если существуют только входящие в него дуги.
3. Узел i называется промежуточным, если существуют и входящие в него, и исходящие из него дуги.
Обозначим:  - множество истоков сети.
- множество истоков сети.
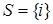 - множество стоков сети.
- множество стоков сети.
 - множество промежуточных узлов сети.
- множество промежуточных узлов сети.
Очевидно, что 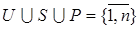 . Задача будет иметь решение лишь в том случае, если в каждом узле – источнике не будет недостатка продукции
. Задача будет иметь решение лишь в том случае, если в каждом узле – источнике не будет недостатка продукции  , а в каждом узле- стоке не будет излишков
, а в каждом узле- стоке не будет излишков 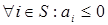 . Для каждого промежуточного узла запас продукции может быть любым
. Для каждого промежуточного узла запас продукции может быть любым  .
.
Введем дополнительные обозначения:
 - множество всех дуг сети,
- множество всех дуг сети,
 - множество дуг, входящих в узел i.
- множество дуг, входящих в узел i.
 - множество дуг, исходящих из узла i.
- множество дуг, исходящих из узла i.
Пусть 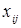 - объем перевозок по дуге
- объем перевозок по дуге 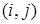 . Тогда ММ ТЗ в сетевой постановке запишется:
. Тогда ММ ТЗ в сетевой постановке запишется:
 (1)
(1)
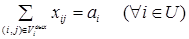 (2)
(2)
 (3)
(3)
 (4)
(4)
 (5)
(5)
В ММ целевая функция (1) выражает суммарную стоимость перевозок на сети. Ограничения (2) требуют вывозить все излишки продукции из узлов-истоков, а ограничения (3) – потребности всех узлов-стоков д.б. удовлетворены. Ограничения (4) для промежуточных узлов отражает тот факт, что разность между объемами вывозимой и ввозимой продукции должна равняться запасу продукции в этом узле (если в узле имелся избыток, то он будет вывезен, если недостаток- он удовлетворен).
ММ (1)-(5) относится к классу ЗЛП и может быть решена стандартными методами решения ЗЛП. Однако, если учитывать особенности ограничений (2)-(5), можно эту задачу свести к модели КТЗ. Тогда модель (1)-(5) будет решаться более эффективно методом потенциалов.
Действительно, уравнения (2) аналогичны уравнениям для пунктов производства КТЗ, т.е. суммарный объем вывоза продукции из узлов-истоков должен равняться запасу продукции в этих узлах. Также и уравнения (3) аналогичны уравнениям для пунктов потребления КТЗ, т.е. суммарный объем ввозимой в узлы-стоки продукции должен равняться нехватке продукции в этих узлах. Однако ограничения (4) выводят данную модель за рамки КТЗ.
|
|
|
Преобразуем данные ограничения таким образом, чтобы они не выводили задачу за рамки КТЗ.
Будем считать, что в каждом промежуточном пункте 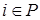 возможна перевозка
возможна перевозка  со стоимостью перевозки единицы продукции
со стоимостью перевозки единицы продукции 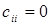 . Также введем обозначения
. Также введем обозначения  - буферный запас, т.е. общий объем излишков продукции.
- буферный запас, т.е. общий объем излишков продукции.
Теперь уравнение (4) перепишем в виде:
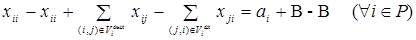 (6)
(6)
Разобьем это уравнение на два:
 (7)
(7)
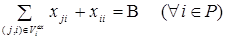 (8)
(8)
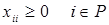 (9)
(9)
Уравнение (7) аналогично уравнениям (2), т.е. объем вывозимой продукции из узла 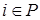 равен имеющемуся там запасу
равен имеющемуся там запасу 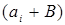 . Уравнение (8) аналогично уравнениям (3), т.е. объем ввозимой продукции в узел
. Уравнение (8) аналогично уравнениям (3), т.е. объем ввозимой продукции в узел 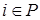 равен потребности этого узла В.
равен потребности этого узла В.
Теперь вместо исходной модели рассмотрим ММ (1)-(3), (5), (7)-(9). Это модель КТЗ, в которой пунктами производства являются все источники  с объемами производства
с объемами производства  и все промежуточные пункты
и все промежуточные пункты 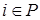 с объемами производства
с объемами производства 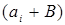 , а пунктами потребления являются все стоки
, а пунктами потребления являются все стоки 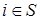 с объемами потребления
с объемами потребления  и все промежуточные пункты с объемами потребления В.
и все промежуточные пункты с объемами потребления В.
Допустим, эта модель КТЗ решена и найдены оптимальные значения 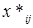 и
и  . Будут ли значения
. Будут ли значения 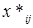 и
и  образовывать решение исходной модели (1)-(5). ДА! Положительный ответ на этот вопрос дает тот факт, что задача (1)-(5) эквивалентна задаче (1)-(3), (5), (7)-(9). Покажем, что это действительно так.
образовывать решение исходной модели (1)-(5). ДА! Положительный ответ на этот вопрос дает тот факт, что задача (1)-(5) эквивалентна задаче (1)-(3), (5), (7)-(9). Покажем, что это действительно так.
Пусть 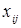 удовлетворяет ограничениям (2)-(5), тогда они удовлетворяют ограничениям и второй задачи (2),(3), (5), (7)-(9). Из уравнения (8) следует, что
удовлетворяет ограничениям (2)-(5), тогда они удовлетворяют ограничениям и второй задачи (2),(3), (5), (7)-(9). Из уравнения (8) следует, что
 (10)
(10)
Знак ³0 следует из того, что суммарный объем ввоза в любой узел не может быть больше буферного запаса В. Т.о. выполняется ограничение (9).
|
|
|
Подставляя (10) в (7), получим тождество:
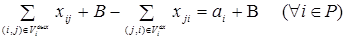 (11)
(11)
т.е. получим уравнение (4), которое удовлетворяется в силу того, что 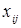 удовлетворяет ограничениям (4). Следовательно,
удовлетворяет ограничениям (4). Следовательно, 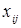 удовлетворяет и ограничениям (7)-(9). Остальные ограничения (2), (3) являются общими для обеих задач. Следовательно, допустимые планы
удовлетворяет и ограничениям (7)-(9). Остальные ограничения (2), (3) являются общими для обеих задач. Следовательно, допустимые планы 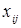 исходной задачи являются допустимыми и для (1)-(3), (5), (7)-(9).
исходной задачи являются допустимыми и для (1)-(3), (5), (7)-(9).
Аналогично доказывается, что если 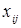 и
и  удовлетворяют ограничениям второй задачи, то они удовлетворяют и ограничениям первой задачи (1)-(5). Для этого достаточно вычесть из (7) уравнение (8). В результате получается уравнение (4).
удовлетворяют ограничениям второй задачи, то они удовлетворяют и ограничениям первой задачи (1)-(5). Для этого достаточно вычесть из (7) уравнение (8). В результате получается уравнение (4).
В обеих задачах минимизируется одна и та же целевая функция. Т.О. (1)-(5) эквивалентна (1)-(3), (5), (7)-(9).
Сравнение методов путей минимальной стоимости и буферного запаса.
При методе поиска кратчайшего пути пунктами производства являются пункты с положительными запасами, а пунктами потребления – с отрицательными. Обычно таких узлов в сети значительно меньше общего числа узлов. Поэтому получаемая в результате КТЗ имеет меньшую размерность, чем при методе буферного запаса. Так как в методе БЗ промежуточные пункты выступают и как пункты производства, и как пункты потребления. Однако в первом случае необходимо предварительно решать столько задач поиска кратчайших путей, сколько имеется в сети пар узлов с положительными и отрицательными запасами.
Кроме того, очень часто встречаются ТЗ, в которых наложены ограничения на пропускную способность дуг:
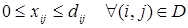 .
.
При использовании метода буферного запаса наличие таких ограничений легко учитывается, а при использовании метода путей минимальной стоимости приходится вводить доп. ограничения, выводящие задачу за рамки КТЗ.
Задача поиска кратчайшего пути на транспортной сети.
Постановка задачи. Пусть дана некоторая транспортная сеть как совокупность узлов с номерами 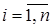 и множества дуг D, соединяющих между собой некоторые узлы сети. Длина дуги
и множества дуг D, соединяющих между собой некоторые узлы сети. Длина дуги  равна
равна  . На сети выделены узел r- начало пути, и узел s- конец пути. Требуется найти путь из узла r в узел s, имеющий минимальную длину, т.е. кратчайший путь.
. На сети выделены узел r- начало пути, и узел s- конец пути. Требуется найти путь из узла r в узел s, имеющий минимальную длину, т.е. кратчайший путь.
Построение ММ. Для составления ММ задачи вводится переменная  .
.
Тогда ММ задачи будет иметь вид:
 (1)
(1)
 (2)
(2)
 (3)
(3)
 (4)
(4)
 (5)
(5)
В этой модели целевая функция (1) определяет длину пути, которая должна быть минимальной. Ограничение (2) требует, чтобы в рассматриваемый путь из r в s входила только одна дуга, исходящая из r. Условие (3) представляет собой условие непрерывности пути, означающее, что если путь входит в какой-либо узел пути (кроме начального и конечного), то он обязательно должен из него выходить. Или, если путь не заходит в узел, то он и не должен из него выходить. Условие (4) говорит о том, что путь кончается в s, т.е. в рассматриваемый путь из r в s входит только одна дуга, входящая в s.
|
|
|
Таким образом, задача о кратчайшем пути свелась к ММ (1)-(5), которая относится к классу задач булевского программирования. Самый простой (но не самый эффективный) способ ее решения состоит в рассмотрении ее как транспортной задачи в сетевой постановке. Действительно, ограничения (2)-(4) аналогичны ограничениям транспортной задачи с единственным пунктом r с положительным запасом 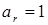 и с единственным пунктом s с отрицательным запасом (потребностью)
и с единственным пунктом s с отрицательным запасом (потребностью)  . Промежуточные узлы
. Промежуточные узлы  имеют нулевой запас
имеют нулевой запас 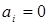 . В свою очередь эту задачу методом буферного запаса можно привести к КТЗ, в которой в качестве пунктов производства выступают узел r и все промежуточные узлы с запасом продукции, равным буферному запасу
. В свою очередь эту задачу методом буферного запаса можно привести к КТЗ, в которой в качестве пунктов производства выступают узел r и все промежуточные узлы с запасом продукции, равным буферному запасу  , а в качестве пунктов потребления – s с потребностью
, а в качестве пунктов потребления – s с потребностью 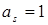 и все ром. узлы с запасом продукции
и все ром. узлы с запасом продукции  . В результате приведения к КТЗ получаем модель задачи о назначениях, где заказы- это пункты производства, а исполнители- это пункты потребления.
. В результате приведения к КТЗ получаем модель задачи о назначениях, где заказы- это пункты производства, а исполнители- это пункты потребления.
Однако существует более эффективный метод решения задачи (1)-(5), основанный на рассмотрении двойственной задачи.
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 455; Нарушение авторских прав?; Мы поможем в написании вашей работы!