
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Курс лекций
|
|
|
|
Новочеркасск 2006
УДК 519.683(076.5)
Рецензент д.т.н., профессор В.Я. Шпицер
Составители: д.т.н., прфессор Кривин В.В.
Основы теории управления: Курс лекций. /Волгодонский ин-т ЮРГТУ. Новочеркасск: ЮРГТУ(НПИ), 2004. 68 с.
Методические указания содержат курс лекций по дисциплине «Основы теории управления».
Предназначены для студентов 1 курса всех форм обучения специальности «Информационные системы и технологии».
ã Волгодонский институт ЮРГТУ, 2006
ã Кривин В.В. 2006
СОДЕРЖАНИЕ
Понятие об управлении. Роль информации в управлении
Для осуществления различных технологических процессов необходимо, чтобы величины, которые характеризуют эти процессы, удовлетворяли определенным условиям. Создание условий, обеспечивающих требуемое протекание процессов, называется управлением.
Управление направлено на достижение определенной цели. Системы, в которых протекает процесс, подлежащий управлению, называются объектами управления (ОУ).
Рассмотрим пример управления движением катера по реке:
Видя берега, указатели фарватера и направление, по которому движется катер, рулевой принимает решение о том, насколько нужно изменить курс, повернуть руль, чтобы двигаться к указанной цели.
В процессе управления можно выделить следующие элементы:
Ø Получение информации о цели управления (маршрут движения)
Ø Получение информации о результате управления (положение катера, фарватер, источником информации является зрение)
Ø Анализ полученной информации и принятие решения о требуемых управляемых действиях (происходит в голове)
Ø Исполнение принятого решения (поворот руля)
Если реализация всех элементов процесса управления осуществляется специально созданными техническими средствами без непосредственного участия человека, то такое управление называется автоматическим.
|
|
|
Когда управление осуществляется совместными действиями технических устройств и человека, то такое управление называется автоматизированным.
Автоматическим регулированием называется поддержание постоянной или изменение по заданному закону некоторой величины, характеризующей процесс.
Автоматическим управлением называется автоматическое осуществление совокупности воздействий, выбранных из множества возможных на основании определенной информации и направленных на поддержание и улучшение функционирования управляемого объекта в соответствии с целью управления.
Совокупность объекта управления и управляемого устройства (регулятор) называется системой автоматического управления (САУ).
Любой процесс управления – это процесс переработки информации, формой представления которой является сообщение (текст, численные/графические данные…). Сообщение отображается сигналом, которым является некоторая изменяющаяся величина любой природы.
Объект автоматического управления.
Состояние объекта или системы характеризуется совокупностью переменных величин, называемых параметрами состояния.
Переменные, характеризующие состояние ОУ, по которым ведется управление, называют управляемыми переменными.
Величины, характеризующие внешнее влияние на объект, называют воздействиями или вход.
Воздействия на объект, вырабатываемые устройством управления, называются управляющими воздействиями.
Воздействие на объект, не зависящее от системы управления, называют возмущающим воздействием (возмущение).
Различают 2 вида возмущения:
1. нагрузка
2. помехи
Нагрузкой является внешнее воздействие, приложенное к управляемому объекту, не зависящее от управляющего устройства и являющееся причиной изменения режима работы объекта управления.
|
|
|
Помехи – это внешние воздействия на отдельные устройства или объекты управления, не содержащие информации, необходимой для управления.
Нагрузка и помехи всегда образуют смесь полезного сигнала и так называемого шума.
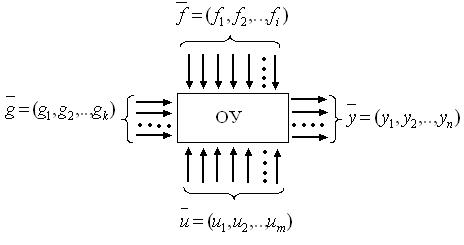
Совокупность управляемых (выходных) переменных обозначаются 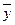 , управляющих –
, управляющих – 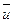 , задающих воздействий –
, задающих воздействий – 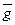 и возмущающих воздействий –
и возмущающих воздействий – 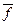 .
.
Если считать, что в системе осуществляется управление всеми координатами состояния системы, то совокупность входных воздействий 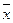 (в объект) и выходных воздействий
(в объект) и выходных воздействий 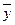 (из объекта) совпадают.
(из объекта) совпадают.
В общем случае 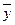 является некой нелинейной функцией управляющих переменных (
является некой нелинейной функцией управляющих переменных (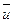 ,
, 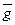 ) и внешних воздействий
) и внешних воздействий 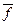 .
.
Правило и функциональная зависимость, в соответствии с которыми управляющее воздействие 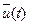 , называемое законом управления, может быть представлено как функция:
, называемое законом управления, может быть представлено как функция:
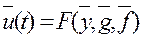 , где
, где
F – некоторая в общем случае нелинейная векторная функция от управляемых переменных 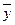 , возмущающих воздействий
, возмущающих воздействий 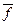 и задающих воздействий
и задающих воздействий 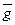 .
.
Каждый ОУ может рассматриваться в условиях статики динамики. В условиях статики компоненты векторов 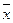 и
и 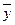 являются постоянными величинами. При изучении динамики объекта исследуется зависимость компоненты вектора
являются постоянными величинами. При изучении динамики объекта исследуется зависимость компоненты вектора 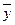 от времени,
от времени, 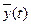 . Параметры объекта могут быть сосредоточенными (постоянными по всем геометрическим координатам) и распределенными (переменными) хотя бы по одной координате.
. Параметры объекта могут быть сосредоточенными (постоянными по всем геометрическим координатам) и распределенными (переменными) хотя бы по одной координате.
Для систем, которые можно описать дифференциальным уравнением, можно записать:
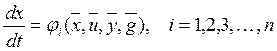
Чтобы решить эту систему уравнений, должны быть заданы начальные условия. Если такая система уравнений может быть сведена к системе линейных д.у., то объект называется линейным. При описании объекта системой нелинейных д.у., объект относят к нелинейным.
Объект может быть:
ü устойчивым

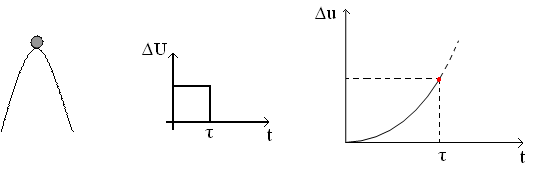
ü неустойчивым
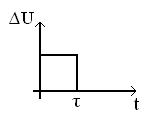
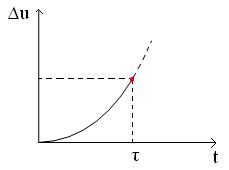
ü нейтральным


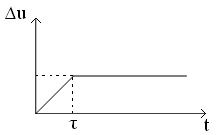
Координата у в устойчивом объекте возвращается в исходное состояние после воздействия ∆U продолжительностью τ. В неустойчивом объекте после окончания воздействия ∆U отклонение от начальной величины управляемой координаты у продолжает увеличиваться. Нейтральными являются объекты, в которых после окончания воздействия устанавливается новое состояние равновесия, которое зависит от произведенного воздействия.
|
|
|
Принципы автоматического управления.
Системы управления (СУ) делятся на замкнутые и разомкнутые. В разомкнутой системе управления управляющее воздействие вырабатывается на основе информации о величине возмущающих воздействий, характеристиках объекта и цели управления. В замкнутой системе управляющее воздействие вырабатывается на основе информации о характеристиках объекта, цели и результатов управления. В таких системах осуществляется замкнутый цикл передачи воздействий, то есть значение управляемой величины на выходе объекта влияет на значение управляющей величины на его входе, то есть эта система с обратной связью.
Рассмотрим объект:
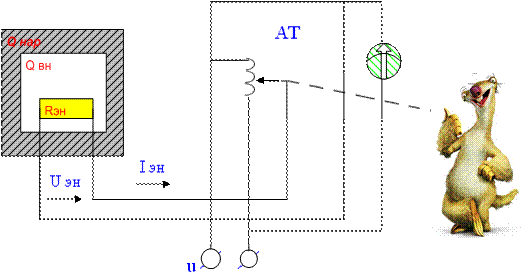
Qвн – температура внутри печи; средняя температура – управляемый параметр.
Если принять Qвн одинаковой по всему объёму, то можно считать такую печь объектом с сосредоточенными параметрами.
Возмущающими воздействиями являются колебания напряжения в сети Uc, изменение сопротивления нагревающего элемента Rэн, изменение теплоемкости и теплопроводимости печи, а так же температура окружающей среды Qнар. Пусть основным возмущающим воздействием является напряжение питающей сети Uc, а остальными возмущающими воздействиями пренебрежем, считая их малыми. Оператор, зная в этом случае, что Qвн зависит от Uc, меняя положение движка автотрансформатора, устанавливает требуемое значение Uэн, тем самым компенсируя влияние возмущающего воздействия. При этом заметим, что температура в печи ему не известна. Основным недостатком разомкнутых систем является то, что для точного управления необходимо примерять и компенсировать отдельно влияние каждого возмущающего воздействия. Достоинством таких СУ является их относительная простота.
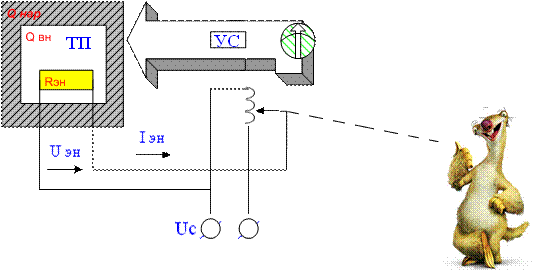
В замкнутой системе, например, при помощи термопары, измеряется температура печи Qвн и, если она меньше заданной, то оператор увеличивает электронагревание (Uэн). Делает он это с помощью ручки автотрансформатора, и наоборот, если Qвн больше заданной.
|
|
|
Если обозначить требуемый закон изменения управляемой величины как g(t), то второй принцип автоматического управления построен на использовании для управления объекта величины
E(t)= g(t)-y(t)
называемой ошибкой или рассогласованием. Величина ε(t)=y(t)-g(t) отличается от Е(t) знаком и называется отклонением.
Принцип управления, основанный на использовании отклонения ε(t) для формирования управляющего воздействия U(t), называется управлением по отклонению. Для его реализации необходимо измерить управляемую величину y(t), сравнить её с задающим воздействием g(t) и в зависимости от величины ε(t) или E(t) осуществить управляющее воздействие на объект.
При E(t) больше нуля, управляющее воздействие должно увеличить управляемую величину у, при E(t) меньше нуля – уменьшить у.
При E(t)=0 управляемая величина имеет требуемое значение и управляющее воздействие u(t)=0.
Функциональная схема системы управления.
Системы автоматического управления (САУ) являются сложными комплексами взаимодействующих технических устройств и элементов, работающих на различных физических принципах.
Графическое изображение САУ позволяет отвлечься от конкретной физической природы элементов реальной системы и даёт наглядное представление об исследуемой системе.
Функциональная схема – схема, отображающая взаимодействие элементов в процессе работы СУ.
Элементы отображаются в виде прямоугольников, а вход и выход в виде прямых линий со стрелками, указывающими направление передачи воздействия.
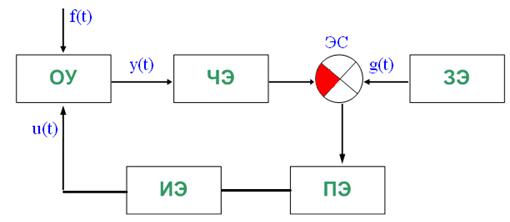
Всё множество элементов СУ может быть разбито на несколько типов:
ОУ – объект управления
ЧЭ – чувствительный элемент (датчик); формирует сигнал, пропорциональный исследуемому параметру.
ЭС – элемент сравнения, осуществляет сравнение выходной управляемой величины у(t) с требуемым значением g(t).
ЗЭ – задающий элемент, задаёт величину управления или преобразует сигнал чувствительного элемента.
ПЭ – промежуточный элемент, служит для увеличения или преобразования сигнала ЧЭ.
Элемент сравнения является сумматором. Сектор, к которому суммируемая величина подводится со знаком «+», не зачерняется, а если со знаком «-», то зачерняется.
Классификация систем автоматического управления.
Большое разнообразие используемых в технике САУ требует использования различных признаков их классификации.
В зависимости от назначения САУ делят на системы стабилизации, программного управления и следящие системы.
Системы стабилизации – предназначены для поддержания постоянного значения управляемой величины у(t). В этих системах задающее воздействие g(t)=g0=const.
В свою очередь в зависимости от того, используются или не используются дополнительные источники энергии, эти системы делятся на:
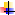 Системы прямого действия – системы, в которых регулируемый орган перемещается непосредственно чувствительным элементом.
Системы прямого действия – системы, в которых регулируемый орган перемещается непосредственно чувствительным элементом.
При h=h0 клапан запирает приток жидкости. Величина h0 задает требуемое значение регулируемой величины.
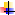 Системы непрямого действия – системы, в которых используется усилитель, получающий энергию извне от дополнительного источника.
Системы непрямого действия – системы, в которых используется усилитель, получающий энергию извне от дополнительного источника.
Системы программного управления – предназначены для изменения управляемой величины у(t) по заранее заданной программе, называемой программой управления.
В таких системах задающее воздействие является известной функцией времени g=g(t) или некоторой другой величины к, g=g(k).
Следящие системы – предназначены для изменения управляемой величины у(t) по закону g(t), который заранее не известен.
По характеру зависимости регулируемой величины от возмущающего воздействия в установившемся режиме системы автоматического регулирования (САР) делятся на:
Предел, к которому стремится ошибка системы регулирования с течением времени, называется установившейся ошибкой:
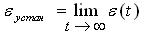
Система регулирования называется статической по отношению к данному внешнему воздействию, если εустан, обусловленная этим воздействием, отлична от «0». САР называется астатической по отношению к какому-либо внешнему воздействию, если εустан, обусловленная этим воздействием, равна «0».
Изобразим зависимость регулируемой величины у от величины возмущающего воздействия f:
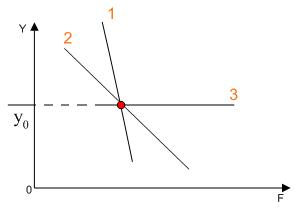
-Кривая 1 имеет место при отсутствии регулятора
-Кривая 2 характерна для статической системы регулирования
-Кривая 3 характерна для астатической системы регулирования
Эту классификацию можно продолжить, например, системы управления делятся на:
§ одноконтурные и многоконтурные
§ импульсные и аналоговые
§ цифровые
§ оптимальные
§ адаптивные и другие.
Задачи теории автоматического управления (ТАУ)
ТАУ изучает общие принципы построения автоматических систем и методы их исследования независимо от физической природы процессов, протекающих в них. ТАУ является теоретической базой создания автоматических систем в различных областях техники.
Основной задачей ТАУ является исследование статических и динамических свойств систем, а также разработки систем, удовлетворяющих заданным технических требованиям.
В ТАУ исследуются 2 основные задачи:
1. Анализ САУ – исследуется уже существующий объект
2. Синтез САУ – требуется на основе знаний и опыта создать несуществующий объект.
МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ САУ
Моделирование систем.
Одним из основных методов исследования систем является моделирование – исследование некоторого процесса при помощи модели.
Моделью данного процесса является некий процесс, имеющий с данным общие свойства, что позволяет использовать модель изучения свойств моделируемого процесса.
Используются физические и математические методы моделирования процессов.
При использовании физического моделирования процессы, протекающие в модели и оригинале, имеют одинаковую физическую природу. Физическая модель может отличаться размерами, скоростью движения, материалами и т.д.
Математическая модель – система математических отношений, описывающих изучаемый процесс или систему.
Математическая модель является абстракцией, которую можно изучать математическими методами.
Аналитические методы исследования наиболее эффективны, когда система (объект) описывается системой линейных д. у. (чрезвычайно редкий случай).
Разбиение систем на звенья.
При построении функциональной схемы систем управления мы разбивали систему на элементы направленного действия в соответствии с функциями, которые они выполняют.
Для получения математического описания системы, её расчленяют на элементы направленного действия – звенья так, чтобы можно было сравнительно просто получить их математическое описание.
Звено – часть системы, которая осуществляет некоторое преобразование входной величины в выходную. В отличие, от функционального элемента, звено не обязательно конструктивно или схемно оформлено.
Если разбить систему на звенья направленного действия, то математическое описание каждого звена может быть выполнено без учета его связей с другими звеньями системы. При этом математическое описание всей системы может быть получено, как совокупность составленных независящих друг от друга уравнений звеньев системы и уравнений связи между ними.
Уравнения связи – уравнения, отражающие характер передачи воздействий между звеньями системы.
В результате разбиения системы на звенья, получается структурная схема системы.
Структурная схема системы – схема, показывающая, из каких звеньев состоит система, и как эти звенья соединены между собой.
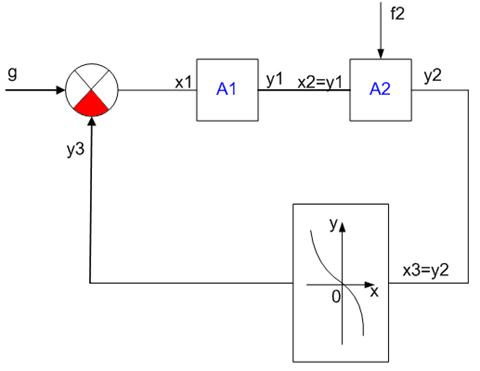
Схема состоит из 3-х звеньев. Зависимость между y1 и х1 задана выражением А1. Зависимость между y2 и х2 – выражением А2. Для третьего звена у3 и х3 – в виде графика.
Внешнее возмущающее воздействие на второе звено показано стрелкой f2. ЭС (суммирующее звено), его выходная величина х1=g – y3.
Статические и динамические характеристики звеньев систем.
Уравнения звеньев систем составляются на основе тех физических законов, которые характеризуют их поведение (законы механики, электротехники, оптики и т.п.).
Уравнения, описывающие поведения звеньев, могут быть алгебраическими, дифференциальными и интегральными. Как правило, это дифференциальные уравнения.
Статическая характеристика звена представляет собой зависимость между входной x и выходной y величинами в установившемся режиме при различных постоянных значениях внешнего воздействия f (f(t)=f).
Рассмотрим пример звена – электродвигатель постоянного тока с независимым возмущением:
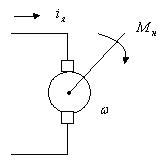
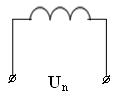
Входная величина – iя, выходная величина – угловая скорость ω. Внешнее воздействие – момент нагрузки на валу Мн и напряжение питания обмотки независимого возбуждения Uп.
Один из многих возможных режимов работы двигателя, при котором Uп=Мн=const, называется номинальным. В этом режиме, как правило, рассчитывается работа двигателя.
При этих значениях 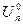 и
и 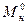 считается, что возмущение f = 0. В этом случае отклонения Мн и Uп от номинальных будут представлять из себя внешнее воздействие.
считается, что возмущение f = 0. В этом случае отклонения Мн и Uп от номинальных будут представлять из себя внешнее воздействие.
В документации на электродвигатель приводят статические характеристики, которые получают экспериментально при производстве двигателей при разных значениях момента нагрузки.
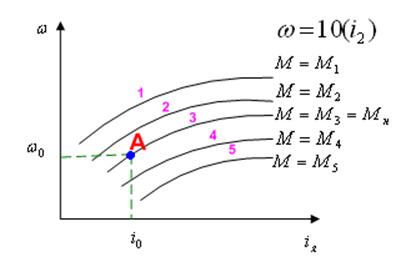
Точка А соответствует номинальному значению тока якоря i0 и угловой скорости ω0. При увеличении нагрузки на валу (Мн < М0) статическая характеристика перемещается вниз (кривые 4, 5). При уменьшении нагрузки кривые ω(iя) будут проходить выше (1, 2).
В общем случае зависимость установившегося значения выходной величины y от установившегося значения входной величины x является нелинейной.
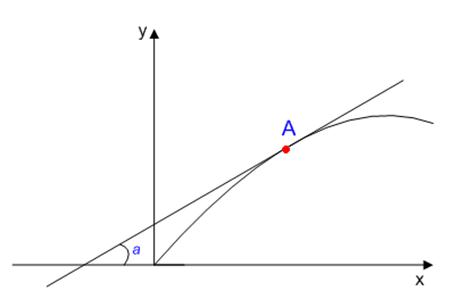
Угловой коэффициент, образуемый касательной к статической характеристике, в любой точке А называется коэффициентом усиления:
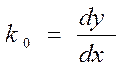
Из рисунка видно, что:
 ,
,
где r – масштабирующий коэффициент, зависящий от масштабов, принятых по осям x и y.
Значение коэффициента k0 служит мерой астатизма звена. Если k0 = ∞, то звено называется астатическим.
Астатическое звено при некотором значении входной величины x = x* находится в равновесии при любом значении выходной величины y.

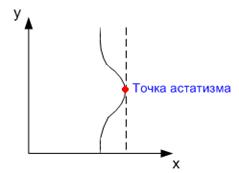
Если на находящееся в некотором состоянии звено подействует некоторое возмущающее воздействие, то оно начнет переходить в некоторое другое состояние. Характер процесса перехода системы из одного состояния в другое определяется динамической характеристикой звена (уравнением движения).
Уравнение движения звена – это уравнение (обычно дифференциальное), определяющее изменение во времени выходной величины звена по заданному изменению во времени его входной величины.
Дифференциальные уравнения могут быть разными для звеньев с сосредоточенными параметрами. Общее уравнение имеет вид:
F(y(n), y(n–1), …,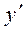 ,у, x(m), x(m–1), …,
,у, x(m), x(m–1), …,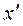 , x, f(g), f(g-1), …,
, x, f(g), f(g-1), …,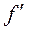 , f) = 0 (1)
, f) = 0 (1)
Где m, n, g – натуральные числа, показывающие высший порядок производной от входной величины x, выходной y и внешнего воздействия f.
На практике, в большинстве случаев m < n, а g < n.
Например, при n = 1 уравнение звена имеет вид:
F(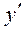 , y, x, f) = 0;
, y, x, f) = 0;
при n = 2:
F(y2,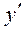 , y,
, y, 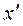 , x,
, x, 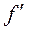 , f) = 0.
, f) = 0.
Уравнение статической характеристики звена можно получить из уравнения (1), положив все производные по времени равными 0, т.е.:
F(0, 0, …, 0, y, 0, 0, …, 0, x, 0, 0, …, 0, f) = 0
Для линейных звеньев (описываемых линейными дифференциальными уравнениями) характерно, что реакция звена на линейную комбинацию воздействий равна той же линейной комбинации реакций звена на каждое влияние в отдельности. Это свойство линейных звеньев выражает собой принцип суперпозиции.
Т.к. решение нелинейных дифференциальных уравнений – задача значительно более сложная, то, когда это возможно, меняют нелинейные дифференциальные уравнения на приближенные линейные. Этот процесс называется линеаризацией.
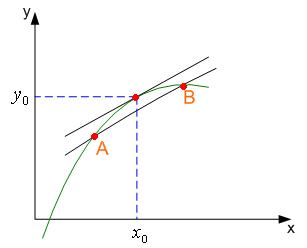
Рис. 1
Если дифференциальное уравнение звена нелинейно из-за нелинейности его статических характеристик, то для линеаризации уравнения необходимо заменить нелинейную статическую характеристику y = ψ(x) на линейную характеристику y=ax + b.
Линеаризация осуществляется при помощи разложения в ряд Тейлора функции y = ψ(x). Это делается в окрестности некоторой точки (x0, y0) и отбрасыванием всех членов разложения, содержащих отклонение ∆y в степени, выше первой. Это означает замену кривой y = ψ(x) касательной в точке (x0, y0). В отдельных случаях линеаризация осуществляется путем проведения секущей между точками А и В (Рис.1).
Рассмотрим процесс линеаризации нелинейного уравнения звена при помощи разложения в ряд Тейлора на примере элемента, поведение которого описывается дифференциальным уравнением вида:
F(y”, y’, y, x,) = 0 (1)
Статическая характеристика такого звена описывается уравнением:
F(0, 0, y, x,) = 0
Если x0, y0 – некоторые установившиеся состояния, то координаты x и y можно записать в виде:
x = x0 + ∆x;
y = y0 + ∆y,
Где ∆x и ∆y – отклонения координат x и y от установившегося состояния.
Уравнение (1) в отклонениях имеет вид:
F(∆y”, ∆y’, y0 + ∆y, x0 + ∆x) = 0
Раскладывая левую часть уравнения в ряд Тейлора относительно точки установившегося состояния с координатами (0, 0, x, y), получим:
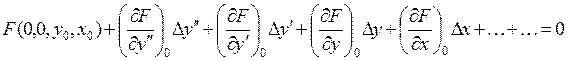 (2)
(2)
Индекс «0» означает, что производные берутся в точке x = x0, y = y0, из чего следует, что ∆x=∆y=0. Здесь в уравнении (2) не написаны члены, содержащие отклонения ∆x и ∆y в степени, выше первой. Частные производные в уравнении (2) – это числа, величина которых зависит от вида функции F(y”, y’, y, x,) = 0 и значений x0 и y0.
Полагая отклонения ∆x и ∆y и их производные по времени малыми, отбросим в уравнении (2) все члены, содержащие отклонения ∆x и ∆y, а также их производную в степени, выше первой, получим:
 (3)
(3)
Уравнение (3) является линейным дифференциальным уравнением с постоянными коэффициентами I, II, III, IV.
Необходимым условием линеаризации является разложимость в ряд Тейлора функции:
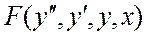 .
.
Уравнение (3) приближенно заменяет уравнение (1) лишь в некоторой малой окрестности точки с координатами (0, 0, x, y). Величина этой окрестности зависит от вида функции 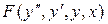 , т.е. от величины производных порядка, выше первого в рассматриваемой точке. Линеаризованное уравнение обычно записывается в каноническом виде:
, т.е. от величины производных порядка, выше первого в рассматриваемой точке. Линеаризованное уравнение обычно записывается в каноническом виде:
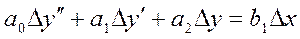 (4)
(4)
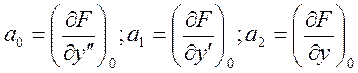
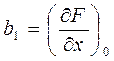
Линеаризация уравнения (1) при помощи разложения в ряд Тейлора означает замену поверхности, описываемой этим уравнением в пространстве переменных 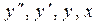 плоскостью касательной к поверхности точки с координатами 0, 0, y0, x0. Ошибка линеаризации тем меньше, чем меньше отклонение друг от друга точек поверхности (1) и точек плоскости (4).
плоскостью касательной к поверхности точки с координатами 0, 0, y0, x0. Ошибка линеаризации тем меньше, чем меньше отклонение друг от друга точек поверхности (1) и точек плоскости (4).
Пример составления дифференциального уравнения звеньев систем управления.
Пример1: составим дифференциальное уравнение двигателя постоянного тока с независимым возбуждением и проведем его линеаризацию:
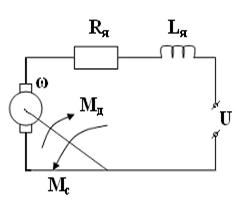
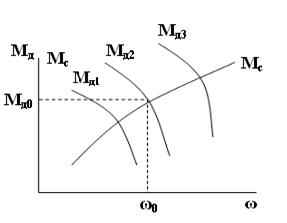
Рис.1.
Мс – момент сопротивления;
Мд – момент движения.
По второму закону Ньютона для вращательного движения уравнение для моментов на валу двигателя имеет вид:
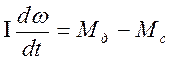 , где (1)
, где (1)
ω – угловая скорость и момент инерции движущихся частей, приведенных к валу;
Мд – вращающий момент
Мс – момент сопротивления на валу двигателя.
Мд представляет из себя функцию двух переменных: скорости вращения и????, а момент сопротивления функцию двух переменных (ω, t):
Мд = Мд(ω, u),
Мс = Мс(ω, t)
Т.к. Мд = Мд(ω, u) и Мс = Мс(ω, t) являются нелинейными функциями (см. рис.1), то уравнение (1) будет нелинейным дифференциальным уравнением.
Для линеаризации уравнения (1) перейдем к уравнению в отклонениях от установившегося режима, т.е. в точке, где Мс0 = Мд0. Пусть при этом ω = ω0 , а u = u0. Разложим нелинейные функции Мд(ω, u), Мс(ω, t) в ряд Тейлора в окрестностях точки ω0 и u0 и отбросим члены, содержащие производные, выше первого порядка:
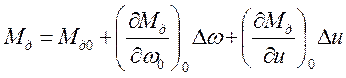 (2)
(2)
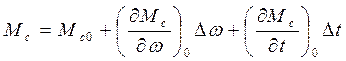 (3)
(3)
Подставив (2) и (3) в (1) получим:
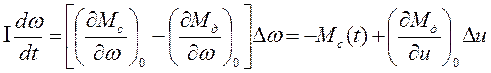 (4)
(4)
В уравнении (4) все члены имеют размерность момента, однако часто бывает необходимо получить уравнение в относительных единицах с безразмерными коэффициентами или с коэффициентами размерности времени в степени, равной порядку соответствующей производной.
Разделим обе части уравнения на номинальное значение Мн:
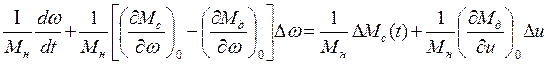
Выберем некоторые величины переменных в качестве базисных.
Для напряжения u удобно взять максимальное значение uмах, а для угловой скорости – её номинальное значение ωн.
Умножив и разделив каждый член уравнения на соответствующую базисную величину, получим:
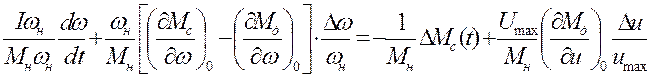
Введем обозначения:
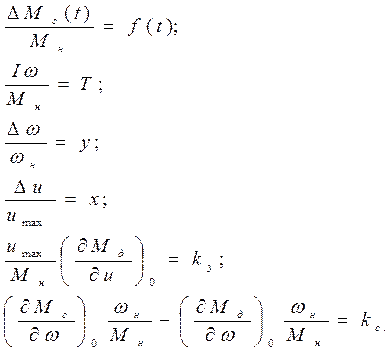
Подставив эти коэффициенты в уравнение, получим:
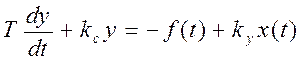
Функция f(t) характеризует возмущающее воздействие, x(t) – управляющее воздействие, y(t) – выходную величину. Коэффициент Т имеет размерность времени (секунды) и называется постоянной времени двигателя.
Отношение ky/kc характеризует зависимость между выходной координатой y и входным воздействием x в установившемся режиме и называется коэффициентом усиления.
Пример2: получение дифференциального уравнения электрического пассивного четырехполюсника.
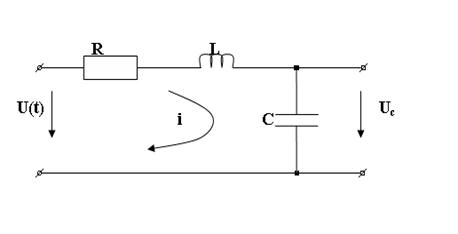
Входной характеристикой является напряжение на входных зажимах u(t), выходной – напряжение на конденсаторе uс. Т.к. цепь является линейной (все элементы цепи линейные), уравнение можно составлять как в отклонениях, так и в безразмерных относительных единицах.
Падение напряжения на резисторе R:
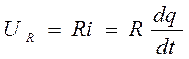 ,
,
Падение напряжения на индуктивности:
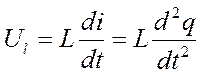
По второму закону Кирхгофа имеем, что приложенное напряжение – это его падение на всех элементах цепи:
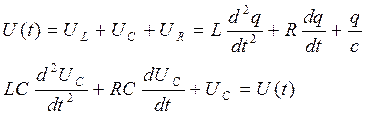
Если обозначить U(t) = x; CL = 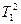 ; RC = T2, то тогда:
; RC = T2, то тогда:
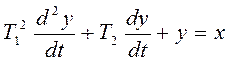
Составление дифференциальных уравнений систем автоматического управления.
Имея дифференциальные уравнения элементов системы и уравнения связи можно получить дифференциальные уравнения всей системы. Однако при исследовании систем управления обычно необходимо знать поведение выходной координаты системы, а не всех её элементов, поэтому можно от системы уравнений описывающих поведение элементов путем исключения промежуточных переменных перейти к одному уравнению. Это уравнение будет содержать только выходную координату системы, а также внешние воздействия. Зная внешнее воздействие, приложенное к системе, и решив дифференциальное уравнение, можно найти реакцию системы управления на эти воздействия. Пусть имеем уравнение объекта управления:
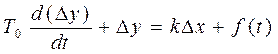 (1)
(1)
и уравнение управляющего устройства:
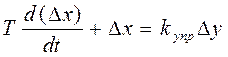 (2)
(2)
Запишем уравнение всей системы управления относительно ∆y. Для этого найдем из уравнения (1) величину ∆x, а также её производную:
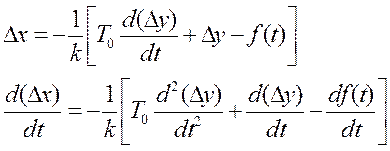
Подставив значение ∆x и  в уравнение (2), получим уравнение системы управления:
в уравнение (2), получим уравнение системы управления:
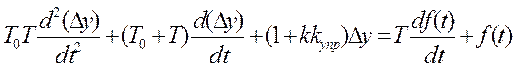
Таким образом, если объект управления и устройство управления описываются дифференциальными уравнениями первого порядка, то система управления в целом описывается дифференциальным уравнением второго порядка.
Пусть теперь объект управления описывается уравнением (1), а устройство управления – дифференциальным уравнением второго порядка:
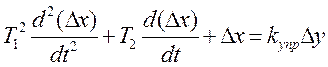 (3)
(3)
Для получения дифференциального уравнения системы управления необходимо получить значение ∆x, а также первую и вторую производные от ∆x:
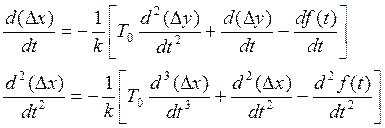
Подставив в уравнение (3) выражение для ∆x, 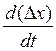 и
и 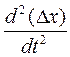 , получим искомое уравнение для всей системы в целом:
, получим искомое уравнение для всей системы в целом:
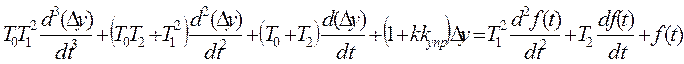
Полученное уравнение третьего порядка устанавливает связь между возмущающим воздействием f на систему и реакцией системы y.
Таким образом, для получения дифференциального уравнения системы, необходимо получить вначале дифференциальное уравнение для объекта управления и устройства управления; исключив из полученных уравнений промежуточные величины, можно получить дифференциальное уравнение относительно интересующих нас величин, но, как правило, эти преобразования очень трудоемки и громоздки.
Для того чтобы упростить решение данной и других задач, в теории автоматического управления вместо рассмотрения величин, характеризующих состояние во времени – оригиналов, рассматриваются соответствующие им изображения, полученные при помощи преобразований Лапласа.
Таким образом, при исследовании и расчетах систем управления широко используются операции исчисления, позволяющие существенно облегчить исследование сложных систем.
Операционное исчисление основывается на преобразованиях Лапласа и Фурье, которые позволяют заменять операции дифференцирования и интегрирования функций на операции более низкого ранга.
Линейные системы.
Система называется линейной, если уравнение динамики и, следовательно, статики этой системы линейны.
К линейным системам применим принцип суперпозиции, который формулируется следующим образом:
Пусть 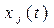 , где j = 1, 2, …, m – некоторые входные сигналы линейной системы, а
, где j = 1, 2, …, m – некоторые входные сигналы линейной системы, а 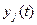 – её реакция на каждый из сигналов, тогда для линейной системы суммарная реакция на суммарный входной сигнал равна:
– её реакция на каждый из сигналов, тогда для линейной системы суммарная реакция на суммарный входной сигнал равна:
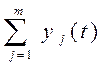
Передаточная функция линейной системы.
Линейные системы в общем случае могут быть описаны дифференциальным уравнением с постоянными коэффициентами вида:
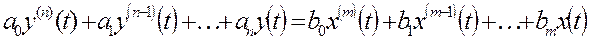
Используя свойство (3), дифференцирование оригинала, к обеим частям уравнения получим:
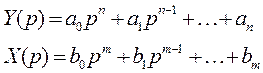
При нулевых начальных условиях найдем связь между лапласовскими изображениями системы y(t) и входного воздействия на систему x(t), получим:
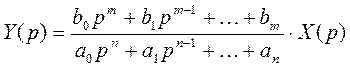
Функция  представляющая собой отношение изображения выходного сигнала линейной системы к изображению входного сигнала при нулевых начальных условиях, называется передаточной функцией линейной системы.
представляющая собой отношение изображения выходного сигнала линейной системы к изображению входного сигнала при нулевых начальных условиях, называется передаточной функцией линейной системы.
Смысл передаточной функции заключается в том, что она представляет собой некий оператор, преобразующий внешнее воздействие на входе в реакцию системы на выходе, т.е.:
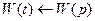
Таким образом, любой линейный объект может быть представлен следующим образом:

В случае, если система управления является замкнутой (охваченной обратной связью), то передаточная функция определяется как:
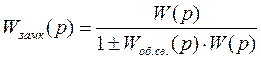 , где (2)
, где (2)
Wоб.св.(p) – передаточная функция управляющего устройства,
Знак «+» - соответствует отрицательной обратной связи, а «-», наоборот.
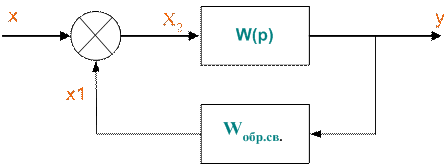
Формула (2) получается из следующих соображений:
по определению передаточной функции имеем:
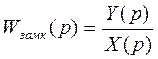 , но
, но
передаточная функция объекта управления:
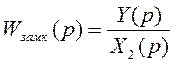 , а
, а
передаточная функция звена обратной связи:
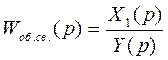
Как видно из рисунка:
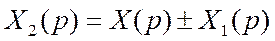 , т.е.
, т.е.
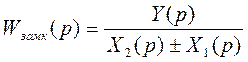 ,
,
разделив числитель и знаменатель на X2(p) получим:
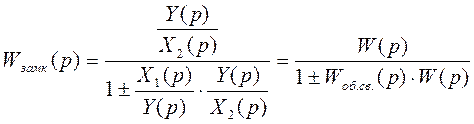
Переходная функция.
Сигнал h(t), полученный на выходе системы при подаче на её вход единичного скачка u(t), называется переходной функцией системы.
Известно, что изображением единичного скачка является:
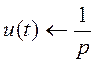 и, следовательно,
и, следовательно,
по определению передаточной функции:
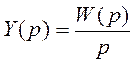 .
.
Связь между передаточной и переходной функцией находиться из формулы:
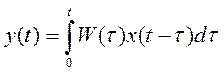
при x(t) = u(t) получим:
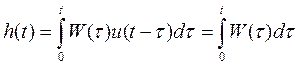
Отсюда имеем:
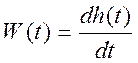 , отсюда видно, что
, отсюда видно, что
оригинал передаточной функции равен производной от переходной функции.
Реакция системы y(t) на произвольное входное воздействие x(t), выраженное через переходную функцию h(t) имеет вид:
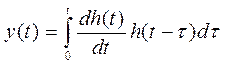
Весовая или импульсная переходная функции системы.
Рассмотрим функцию δ(t), называемую функцией Дирака. В теории управления её называют единичным импульсом. Определим δ(t):
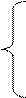 |
 ∞, при t = 0
∞, при t = 0
δ(t) =
0, при t ≠ 0
или
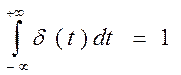
В общем случае, как и функция Хевисайда, функция Дирака является математической абстракцией.
Рассмотрим вспомогательную функцию δ(t, μ):
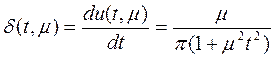
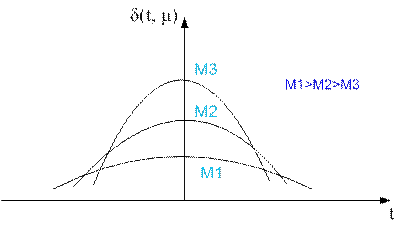
В этом случае функцию δ(t) можно рассматривать как предел функции δ(t,μ) при μ → ∞, т.е.
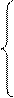 ∞, при t = 0
∞, при t = 0
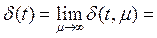
0, при t ≠ 0
Если воспользоваться формальным равенством, то по определению производной получим:
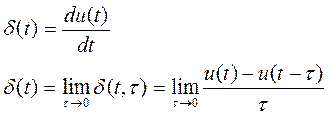
Исходя из формального равенства 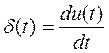 и того, что
и того, что 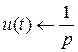 получим:
получим:
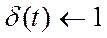 .
.
Сигнал, получаемый на выходе линейной системы при подаче на её вход единичного импульса, называется весовой или импульсной переходной функцией. И так как изображение входного сигнала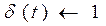 , то по определению передаточной функции:
, то по определению передаточной функции:
Y(p) = W(p),
т.е., переходя от изображения к оригиналу:
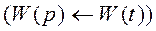
получаем оригинал передаточной функции.
Частотные и логарифмические характеристики линейных систем.
Частотной характеристикой линейной системы или комплексно - частотной функцией линейной системы называется функция W(jω), получаемая из передаточной функции системы подстановкой p = jω.
Физически эта подстановка означает, что сигнал на входе системы является синусоидальным (гармоническим). Частотную характеристику можно представить в виде:
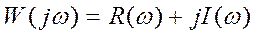 (1)
(1)
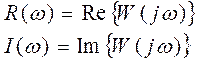
Где R(ω) и I(ω) вещественная и мнимая части комплексно-частотной характеристики соответственно.
Формула (1) показывает, что W(jω) является векторной суммой R(ω) и I(ω) в декартовых координатах на комплексной плоскости. В полярных координатах:
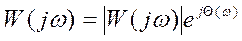 (2),
(2),
где
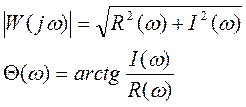
Функции W(ω) и Θ(ω) определяют изменение амплитуды и фазы колебаний на выходе по отношению к амплитуде и фазе колебаний на входе и называются АЧХ и ФЧХ соответственно.
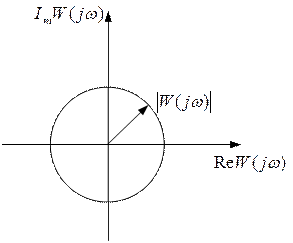
Рассматривая W(jω) как вектор и варьируя частоту входного сигнала ω от 0 до ∞, получаем на комплексной плоскости кривую, описываемую концом этого вектора. Эта кривая называется годографом вектора комплексно- частотной функции или амплитудно-фазовой частотной характеристикой (АФЧХ).
Заметим, что 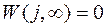
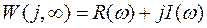
|
|
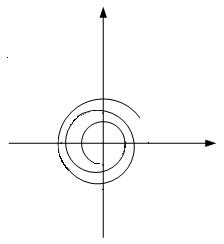
Широкое практическое применение нашли частотные характеристики, построенные в логарифмическом масштабе.
Логарифмируя выражение (2) получаем:
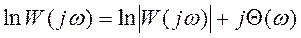
Зависимость 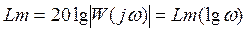 называется логарифмической амплитудно-частотной характеристикой (ЛАЧХ), а Θ = Θ(lgω) – логарифмической фазо-частотной характеристикой (ЛФЧХ).
называется логарифмической амплитудно-частотной характеристикой (ЛАЧХ), а Θ = Θ(lgω) – логарифмической фазо-частотной характеристикой (ЛФЧХ).
ЛАЧХ и ЛФЧХ строятся в логарифмическом масштабе, т.е. по оси абсцисс откладываются логарифмические частоты.
За единицу масштаба принимается декада – это частотный интервал, соответствующий изменению частоты в 10 раз.
По оси ординат при построении ЛФЧХ фаза откладывается в радианах или угловых градусах.
Типовые звенья линейных систем.
Любые сложные системы могут быть представлены как совокупность более простых элементов. Для исследования процессов в реальных системах пользуются идеализированными схемами, которые точно описываются математически и приближенно характеризуют реальные звенья систем в заданном диапазоне частот.
В теории управления вводятся некие типовые звенья, которые характеризуются, в независимости от их конструктивного исполнения, назначения, принципа действия и т.п., только своими передаточными функциями.
Классифицируют эти звенья по виду дифференциальных уравнений, описывающих их работу.
Типы звеньев:
· Описывающиеся линейными алгебраическими уравнениями относительно выходного сигнала:
а) пропорциональные (безынерционные);
б) запаздывающие;
в) дифференцирующие.
· Описывающиеся дифференциальными уравнениями первого порядка с постоянными коэффициентами:
а) инерционно дифференцирующие;
б) инерционные (апериодические, релаксационные);
в) интегрирующие (астатические, нейтральные);
г) интегро – дифференцирующее (упругие).
· Описывающиеся дифференциальными уравнениями второго порядка с постоянными коэффициентами:
а) колебательные;
б) апериодические.
Перечень формул, которые будут использованы для описания характеристик типовых звеньев:
1. Передаточная функция:  ,
,
2. Переходная функция: 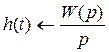 ,
,
3. Весовая функция: 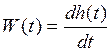 ,
,
4. Частотная характеристика: 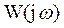 ,
,
5. АЧХ: 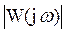 ,
,
6. ФЧХ: 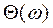 ,
,
7. ЛАЧХ: 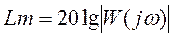 ,
,
8. ЛФЧХ:  .
.
Пропорциональное звено.
Выходной сигнал прямо пропорционален входному. Описывается уравнением:
y(t) = kx(t), где
k – коэффициент усиления.
Примеры: резистивный делитель напряжения, рычажная передача и др.
Переходя к изображениям, имеем:
Ø Передаточную функцию:
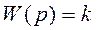
Ø Переходная функция:
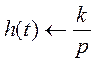 ,
,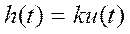
Ø Весовая функция:
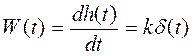
Ø Частотная характеристика:
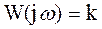
Ø АЧХ:
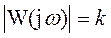
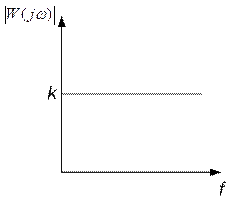
Ø ФЧХ: 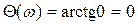 ,
,
Ø ЛАЧХ: 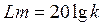 ,
,
Ø ЛФЧХ: 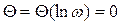 .
.
Принятое описание связи между входной и выходной величинами справедливо только для идеального звена и соответствует реальным звеньям лишь при низких частотах ω, меньших ωверх. При ω > ωверх в реальных звеньях коэффициент усиления kус начинает зависеть от частоты и с её увеличением в ∞ падает до 0.
Запаздывающее звено.
Описывается уравнением:
y(t) = x(t-τ), где
τ – время запаздывания.
Примеры: длинные электрические линии без потерь, тепловые объекты, трубопровод, зубчатые передачи и др.
Переходя к изображениям, имеем:
Ø Передаточная функция: 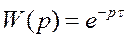
Ø Переходная функция: 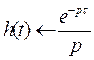 ,
, 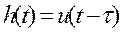
Ø Весовая функция: 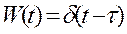
Ø Частотная характеристика: 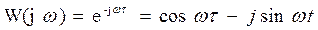
Ø АЧХ: 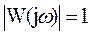
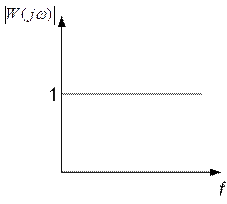
Ø ФЧХ: 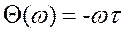
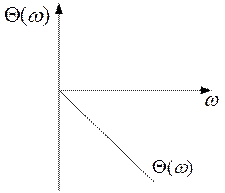
Ø ЛАЧХ: 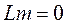
Дифференцирующее звено.
Описывается уравнением:
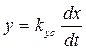 , где
, где
k – коэффициент усиления.
Примеры: конденсатор 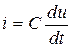 и индуктивность
и индуктивность 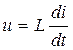 .
.
Переходя к изображениям при нулевых начальных условиях, имеем:
Ø Передаточная функция: 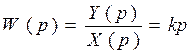 ,
,
Ø Переходная функция: 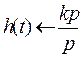 ,
, 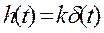 ,
,
Ø Весовая функция: 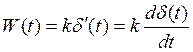 ,
,
Ø Частотная характеристика: 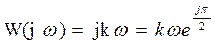 ,
,
Ø АЧХ:  ,
,
Ø ФЧХ: 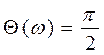 ,
,
Ø ЛАЧХ: 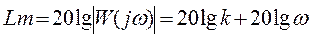 .
.
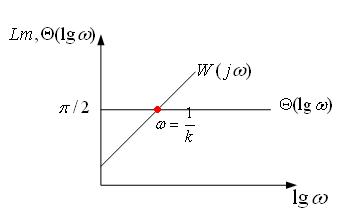
Инерционно-дифференциальное звено.
Описывается дифференциальным уравнением первого порядка:
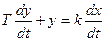 , где
, где
Т – постоянная времени,
k – коэффициент усиления.
При Т→ 0 уравнение переходит к уравнению, описывающему идеальное дифференциальное звено.
Примеры: конденсатор или индуктивность с учетом активного сопротивления цепи.
Переходя к изображениям при нулевых начальных условиях, получим:
Ø Передаточная функция: 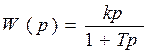 ,
,
Ø Переходная функция: 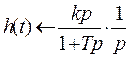 ;
; 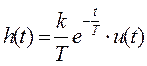 ,
,
Ø Весовая функция: 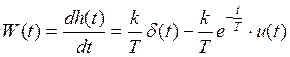 ,
,
Ø Частотная характеристика: 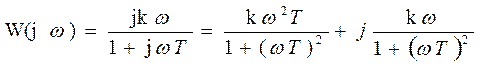 ,
,
Ø АЧХ: 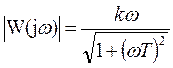 ,
,
Ø ФЧХ: 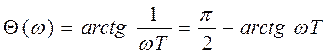 ,
,
Ø ЛАЧХ: 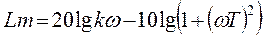 .
.
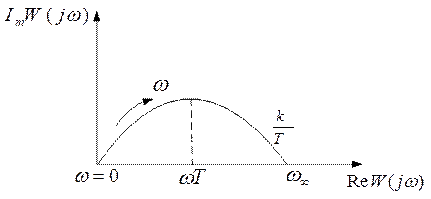
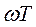 вычисляется при частоте
вычисляется при частоте 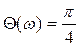
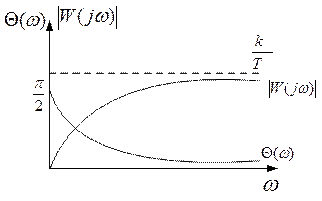
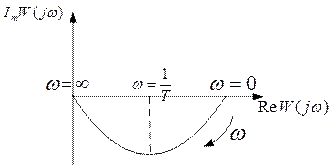
Инерционное звено.
Одно из самых распространенных звеньев. Описывается уравнением:
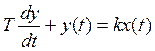 , где
, где
Т – постоянная времени,
k – коэффициент усиления.
Примеры: электродвигатель, термопара.
Переходя к изображениям при нулевых начальных условиях, имеем:
Ø Передаточная функция: 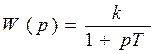 ,
,
Ø Переходная функция: 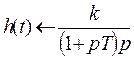 ,
, 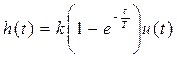 ,
,
Ø Весовая функция: 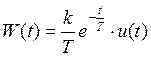 ,
,
Ø Частотная характеристика: 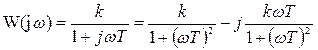 ,
,
Ø АЧХ: 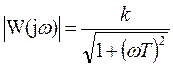 ,
,
Ø ФЧХ: 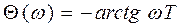 ,
,
Ø ЛАЧХ: 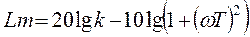 .
.
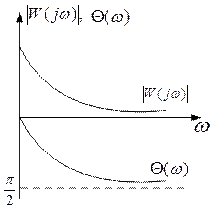
Интегрирующее звено.
Описывается уравнением:
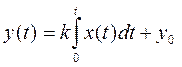 или
или 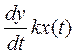 , где
, где
k – коэффициент пропорциональности.
Примеры: вращающийся вал, если входной величиной считать скорость вращения, а выходной – угол поворота вала.
Переходя к изображениям при нулевых начальных условиях, имеем:
Ø Передаточная функция: 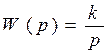 ,
,
Ø Переходная функция: 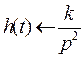 ,
, 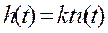 ,
,
Ø Весовая функция: 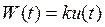 ,
,
Ø Частотная характеристика: 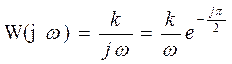 ,
,
Ø АЧХ: 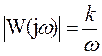 ,
,
Ø ФЧХ: 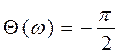 ,
,
Ø ЛАЧХ: 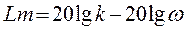 .
.
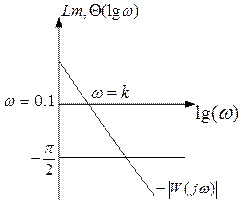
Интегро-дифференцирующее звено.
Описывается дифференциальным уравнением первого порядка:
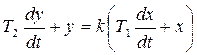 , где
, где
Т1, Т2 – постоянные времени,
k – коэффициент усиления.
В зависимости от 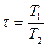 звено будет обладать различными свойствами. Если τ < 1, то звено по свойствам будет приближаться к интегрирующему и инерционному звеньям, если τ > 1, то звено ближе к дифференцирующему и инерционно-дифференциальному звеньям.
звено будет обладать различными свойствами. Если τ < 1, то звено по свойствам будет приближаться к интегрирующему и инерционному звеньям, если τ > 1, то звено ближе к дифференцирующему и инерционно-дифференциальному звеньям.
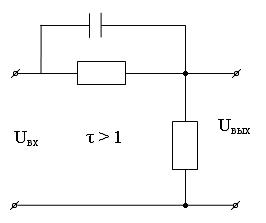
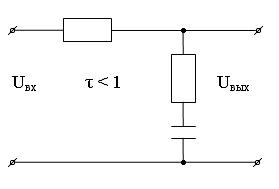
Переходя к изображениям при нулевых начальных условиях, имеем:
Ø Передаточная функция: