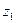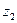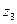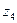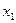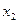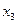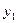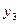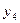КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Понятие о методах дискретной математики
|
|
|
|
Обобщающий аппарат теоретико-множественных представлений позволил объединить ряд методов в единую область - дискретную математику. Рассмотрим эти методы.
Методы моделирования систем с помощью конечных автоматов. Среди детерминистических динамических систем, функционирующих в дискретном времени, исключительно важное место занимают конечные автоматы. Аппарат теории конечных автоматов используется как инструмент анализа и синтеза цифровых вычислительных машин и разнообразных автоматических устройств. В последние годы на его базе успешно развиваются методы автоматизации проектирования объектов этого класса. Хорошо изученные количественные методы и качественная теория конечных автоматов служат образцом для выбора путей и подходов к исследованию динамических систем более общего вида.
Конечный автомат - только одна из схем первичной формализации дискретных устройств и процессов, математическая модель различных объектов материального мира. Это обстоятельство и определяет характер изложения материала.
Конечное множество объектов можно интерпретировать как алфавит, если сами объекты есть основание называть буквами. В качестве букв рассматриваются объекты любой природы: буквы русского или латинского алфавита, цифры, значки, рисунки, фразы, алгоритмы и т.д. Конечная упорядоченная совокупность букв (не обязательно различных) называется словом в данном алфавите.
Конечный автомат представляет собой объект, функционирующий в моменты автоматного времени  ; в каждый момент
; в каждый момент 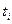 из этой совокупности (множества Т) он находится в одном из возможных состояний
из этой совокупности (множества Т) он находится в одном из возможных состояний 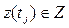 , где
, где  - множество состояний автомата (предполагается конечным). В каждый момент
- множество состояний автомата (предполагается конечным). В каждый момент 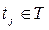 , начиная с
, начиная с  , на вход автомата поступает входной сигнал - одна из букв
, на вход автомата поступает входной сигнал - одна из букв 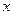 входного алфавита
входного алфавита 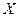 .
.
|
|
|
Автомат следующим образом реагирует на поступление входных сигналов. Во-первых, состояние автомата изменяется в соответствии с одношаговой функцией переходов
 (2.14)
(2.14)
Во-вторых, в каждый момент автоматного времени на выходе автомата появляется выходной сигнал 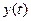 - буква выходного алфавита
- буква выходного алфавита 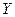 , определяемый функцией выходов
, определяемый функцией выходов
 (2.15)
(2.15)
Конечный автомат может быть задан при помощи таблиц переходов и выходов. В табл. 2.3 и 2.4 описан автомат с входным алфавитом 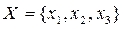 , множеством состояний
, множеством состояний 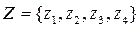 и выходным алфавитом
и выходным алфавитом 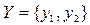 .
.
Таблица 2.3
|
Таблица 2.4 |
Если в автомат, находящийся в состоянии 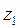 , поступает входной сигнал
, поступает входной сигнал 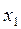 , автомат переходит в состояние
, автомат переходит в состояние 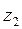 ; выходной сигнал при этом будет
; выходной сигнал при этом будет 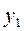 , и т.д.
, и т.д.
Автомат может быть описан при помощи ориентированного графа: состояниям автомата соответствуют вершины графа, а стрелки 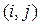 показывают переход из состояния
показывают переход из состояния 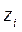 в состояние
в состояние 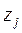 под влиянием входного сигнала
под влиянием входного сигнала 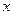 . Соответствующие сигналы (входные и выходные) записываются вдоль стрелок графа. На рис. 2.4 представлен граф для автомата, заданного табл. 2.3 и 2.4.
. Соответствующие сигналы (входные и выходные) записываются вдоль стрелок графа. На рис. 2.4 представлен граф для автомата, заданного табл. 2.3 и 2.4.
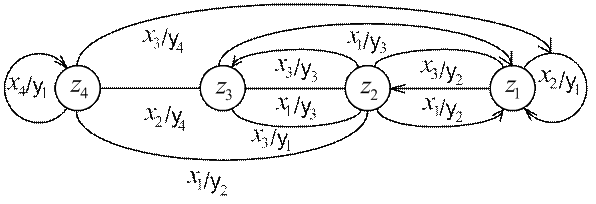
Рис. 2.4
Рассматриваемый конечный автомат называется автоматом Мили.
Для автоматов Мура функция выходов имеет другой вид
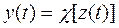 (2.16)
(2.16)
и называется сдвинутой функцией выходов.
В дальнейшем мы будем обозначать автомат 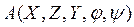 как объект, определяемый множествами
как объект, определяемый множествами 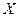 ,
,  ,
, 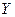 и функциями
и функциями 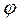 и
и 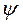 (или
(или 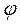 и
и 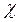 ).
).
Любому входному слову  ,
, 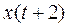 ,…,
,…,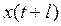 длины
длины 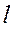 , поступающему в автомат, ставится в соответствие выходное слово
, поступающему в автомат, ставится в соответствие выходное слово 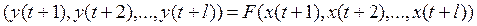 той же длины, определяемое функциями переходов и выходов при условии, что в начальный момент автомат находится в некотором состоянии
той же длины, определяемое функциями переходов и выходов при условии, что в начальный момент автомат находится в некотором состоянии  .
.
Автомат может быть синхронным в том смысле, что моменты 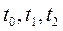 (поступления входных сигналов, изменения состояний и выдачи выходных сигналов) заранее определены. Асинхронные автоматы не имеют «жесткой» тактности; они изменяют свои состояния при поступлении входных сигналов, которые могут появляться в произвольные моменты времени из некоторого интервала. Заметим, что в последнем случае автомат следует скорее рассматривать как объект, функционирующий в непрерывном времени.
(поступления входных сигналов, изменения состояний и выдачи выходных сигналов) заранее определены. Асинхронные автоматы не имеют «жесткой» тактности; они изменяют свои состояния при поступлении входных сигналов, которые могут появляться в произвольные моменты времени из некоторого интервала. Заметим, что в последнем случае автомат следует скорее рассматривать как объект, функционирующий в непрерывном времени.
|
|
|
Теоретико-множественные представления базируются на понятиях множество, элементы множества, отношения множеств.
Понятие множество содержательно эквивалентно понятиям «совокупность», «собрание», «ансамбль», «семейство», «класс» и другим обобщающим понятиям.
Множества задаются:
- списком, перечислением или интенсиональным путем, например, {аi}, где i=1,2,…,n, или <а1,а2,...,аi,...,an>, аiÎА;
- путем указания характеристического свойства множества А, или экстенсиональное задание множества.
Переход от интенсионального способа задания множества к экстенсиональному называют принципом свертывания.
В множестве может быть выделено подмножество В Ì А.
Пустое множество Æ не содержит ни одного элемента.
При использовании теоретико-множественных представлений можно вводить любые отношения. Над множествами задаются операции объединения (È), пересечения (Ç), дополнения (-) и другие.
Между теоретико-множественными описаниями разных систем можно устанавливать соответствия. Для характеристики сходства множеств используют понятия гомоморфизма, изоморфизма, автоморфизма, отношения рефлексивности, симметричности, транзитивности.
Важным является понятие континуума - связного обобщающего множества, в рамках которого осуществляются операции над множествами.
Теоретико-множественные представления, как обобщающий язык математики, явились основой для возникновения новых научных направлений и получения новых результатов (теория чисел, комбинаторика, топология, теория нечетких множеств [24] и прочее).
Система S может быть отображена теоретико-множественной формулой, включающей наборы различных элементов (например, А, В, С), отношений между ними (R), которые могут быть также разделены на подмножества (R1, R2, R3 и т. д.), свойств элементов QA, QB, QC и свойств отношений QR, множествами входных воздействий Х и выходных результатов Y. Тогда теоретико-множественное определение системы будет иметь вид
|
|
|
S = <А, В, С, R, QA, QB, QC, QR, X, Y>. (2.17)
По мере накопления сведений о системе формула (2.10) может измениться и отразить взаимоотношения между группами множеств, например:
S = <{xi}, R1 {aj}, R2 {bk}, R3 {cd}>, (2.18)
а в дальнейшем описание может уточняться.
Могут быть введены подмножества и отношения между ними и их элементами; деление на подмножества может быть повторено неоднократно. Таким образом, с помощью теоретико-множественных представлений может быть отображена многоуровневая структура. Отношения могут быть уточнены в виде набора правил преобразования множеств или подмножеств.
Базовыми понятиями математической логики являются высказывание, предикат, логические функции, кванторы, логический базис, логические законы.
Под высказыванием понимается повествовательное предложение (суждение), которое характеризуется определенным значением истинности.
Алгебра логики, в которой переменная может принимать только два значения истинности («да», «нет»), называется бинарной алгеброй логики Буля.
Предикат - выражение, грамматически имеющее форму высказы-вания, но содержащее переменные некоторых подмножеств, на которых они определены.
При замене переменных элементами соответствующего подмножества предикат обращается в высказывание. Например, "быть Х-м карандашом", где Х может принимать значения "красный","синий" и т. д.
Частным случаем предиката является пропозиционная функция - функция одной или нескольких переменных, принимающих значение в множестве {0,1}.
Из одного или нескольких высказываний можно образовывать новые высказывания или предикаты. Объединение простых высказываний в сложные высказывания производится на основе определенных логических правил (функций).
Кроме логических функций, в логике предикатов имеются еще операции квалификации - кванторы. Это специальные операции, которые служат для выражения общности суждений и связанных с ними понятий и позволяют на формальном языке исчисления предикатов говорить не об одном объекте, а о целом классе объектов.
|
|
|
Полную систему логических функций называют логическим базисом.
Из элементарных функций алгебры логики формируют последовательности действий, отображающие процессы в системе от входа до выхода, т. е. логические алгоритмы.
На рис. 2.5 показан пример логического алгоритма
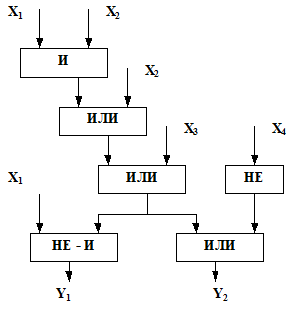
Рис.2.5
Этот же алгоритм может быть записан в виде функций:
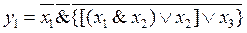 , (2.19)
, (2.19)
 . (2.20)
. (2.20)
Запись алгоритмов может быть произведена в виде функций алгебры логики, в форме таблиц или матриц, "машин Тьюринга", логических схем по А.А.Ляпунову, с помощью рекурсивных функций, на языке нормальных алгоритмов А.А.Маркова, в виде программ для ЭВМ, в форме диаграмм Насси - Шнайдермана [25, 26, 27].
Логические алгоритмы преобразовываются с использованием логических законов. Пример закона А. де-Моргана показан на рис. 2.6.
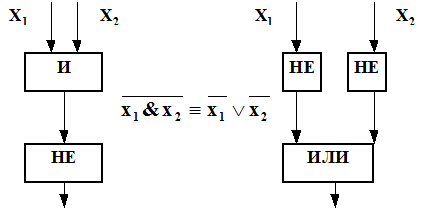
Рис. 2.6
На основе логических представлений возникли и развиваются теории логического анализа и логического синтеза.
Задача логического анализа состоит в описании поведения системы с известной структурой набором системно-логических уравнений в виде функций алгебры логики и исследования полученного логического выражения с целью его минимизации.
Задача логического синтеза заключается в том, чтобы по известному поведению системы определить ее структуру, если она неизвестна или не полностью известна, т. е. сопоставить системе некоторый «автомат» («черный ящик») с известными входными и выходными воздействиями.
Задача логического синтеза сложнее задачи анализа и решается путем последовательных приближений.
Особенности задачи логического синтеза при описании системы логическим автоматом вызвали возникновение и развитие самостоятельной научной дисциплины - теории автоматов.
Логические представления широко применяются при исследовании и разработке автоматов разного рода, автоматических систем контроля, при решении задач распознавания образов.
Лингвистические, семиотические представления также являются методами дискретной математики, однако их включение в эту математику нельзя считать общепризнанным.
Математическая лингвистика возникла во второй половине 19-го века как средство формализованного изучения естественных языков. Активное возрождение этой науки произошло в 50 - 60-е гг. 20-го века и связано с потребностями прикладных технических дисциплин.
|
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 737; Нарушение авторских прав?; Мы поможем в написании вашей работы!