Определение начальных условий алгоритмаЯзвинского при оценке результатов измерения

Алгоритм Язвинского предназначен для определения оценки нестационарных результатов измерения путем адаптивной фильтрации по последовательности скалярных измерений y_k [18, 94]. При этом в качестве модели измерений выбирается модель Гаусса – Маркова [75]

y_k = H _k x _k + v_k,

априорные данные для которой задаются ошибками, сопровождающими измерение, а также начальными условиями x _н. Причем ошибки описываются нормальным законом распределения с нулевым математическим ожиданием и дисперсией D _k, т. е. v_k ~ N (0, D _k). Эти элементы математической постановки задачи оценивания задаются как

Q = .

При этом в качестве критерия оптимизации выбирается критерий максимального правдоподобия для совместной плотности распределения вероятностей x_k и Y ₁ ^k

),

который совпадает с минимумом среднего риска оценивания алгоритма фильтрации.

Значения данного алгоритма определяются соотношениями

x (k | k) = M[ x_k | Y ₁ ^k, 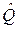] = x (k | k – 1) + K_k v_k;

v_k = y_k – H _k x (k | k – 1).

Данный алгоритм является квазиоптимальным, т.е. вид решения уравнения будет меняться в зависимости от дополнительных ограничений, накладываемых по условию каждой конкретной задачи.

Оценка диагональной матрицы Q требует значительного объема вычислений, связанных с обращением матрицы A.

Алгоритм не предусматривает оценивание матрицы измерительных шумов R.

Для повышения качества полученных оценок используют адаптивный алгоритм с обратной связью по обновленной последовательности, который имеет вид

x (k +1| k +1) = x (k +1| k) + K_{k +1} v (k +1| k);

v (k +1| k) = y_{k +1} – H x (k +1| k);

K_{k +1} = s ⁺ M_v (v (k +1| k) v ^T(k +1| k)^-1;

s ⁺ = (s ^T s)^-1 s ^T;

М_v = 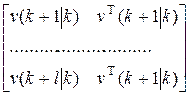; s = .

Как первичный алгоритм Язвинского, так и его модификация требует задания начального условия x _н. Выбор данного параметра алгоритма оценивания является важным этапом определения оцениваемого параметра. Вследствие ограниченности априорных данных на начальных этапах оценивания, а также отсутствия апостериорных данных выбора качественной начальной оценки x _н, критерием ее выбора не может быть точность ее задания. Однако эта оценка должна обеспечивать максимальную сходимость алгоритма уже на начальных этапах его функционирования.

Таким образом, задача выбора начального условия x _н сводится к тому, чтобы при одинаковой дисперсии исходной оценки необходимо выбрать ту начальную оценку, которая при одинаковом объеме статистики обеспечивает максимальную сходимость алгоритма.

Для конкретизации выбора начального значения x ₀ учтем, что аналогично экстремальному свойству нормального закона распределения случайной величины при заданной дисперсии для энтропии Шеннона [96] можно сформулировать экстремальное свойство и для энтропии Кульбака – Лейблера, в соответствии с которым величина нормированного риска R ₁(x, ) достигает свое максимальное значение для нормального закона распределения. Для доказательства этого положения учтем, что плотность вероятности нормально распределенной случайной величины в выражении ее энтропии Шеннона вне знака логарифма может быть замена произвольной плотностью вероятности, поскольку законы распределения сравниваются при нулевом математическом ожидании и при одинаковых дисперсиях:

D = =.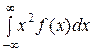

Следовательно, для нормального закона распределения экстремальная энтропия Шеннона равна

H_N [ X ] = = .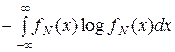

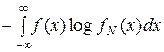Вычтя из данного выражения величину энтропии для произвольного закона распределения, отличающегося от нормального,

H [ X ]= ,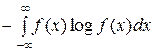

получаем максимальное значение для энтропии Кульбака – Лейблера:

H_N [ X ] – H [ X ] = .

Как показано в работе [3], величина нормированного риска совпадает с выражением для энтропии Кульбака – Лейблера при условии, что величина f_N (x) равна интенсивности риска:

,

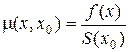где f (x) – плотность распределения начальной оценки оцениваемой случайной величины; S (x ₀) = 1 – F (x ₀), F (x ₀) = .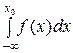

В связи с этим интенсивность риска должна иметь вид нормального закона распределения, т.е.

f_N (x) = ,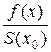

что возможно при условии, когда плотность распределения случайной величины должна носить нормальный закон распределения.

Учтя экстремальное свойство нормального закона распределения нормированного риска, из формулы (1) следует, что в качестве начальной оценки алгоритма Язвинского, при определении оценки по результатам измерения, следует выбирать оценку с нормальным законом распределения

x _н ~ N ((0|0), D (0|0)),

которая обладает предельной асимптотической эффективностью, т.е. обеспечивает уже на первых шагах функционирования алгоритма оценивания предельную скорость его сходимости.

Дата добавления: 2014-01-05