
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Способы преобразования переменных модели измерения
|
|
|
|
Для повышения эффективности и качества модели измерения может быть применен ряд способов преобразования переменных модели измерения.
Способ последовательной селекции переменных модели. Полученные выражения для риска линейной модели контроля показывают необходимость выделения каждой переменной модели. В связи с этим возникает задача их распознавания, которая решается на базе теории распознавания образов [114]. В общем случае контролируемые признаки образов х 1, х 2,..., хN одного класса искажаются помехами, которые сопровождают их контроль. Для каждого класса образов w j, j = 1,..., m известны многомерная (N – мерная) функция плотности вероятности вектора признаков Х, р (Х |w j) и вероятность Р (w j) появления класса w j. На основе этой априорной информации р (Х |w j) и Р (w j), j = 1,..., m функция классификации сводится к минимизации вероятности ошибочного распознавания. Задача классификации образов [113] формулируется в виде задачи статистических решений (испытание m статистических гипотез) с помощью определения решающей функции d (X), где d (X) = di означает, что принимается гипотеза Hi, при которой величина X принадлежит классу w i.
Пусть w1, w2,..., w m обозначают m возможных классов состояний, подлежащих распознаванию, а Х = [ х 1, х 2,..., хN ]T – вектор замеров параметров, где хi представляет собой i – й замер. Если входной образ, представленный вектором параметров Х, принадлежит классу w i, то величина di (X) больше разделяющей функции dj (X), относящейся к классу состояний w j, j = 1,..., m. Если вектор параметров X входного образа принадлежит классу w i, то для всех Х, принадлежащих классу w I, получаем
di (X) > dj (X), i, j = 1,..., m, i ¹ j. (4.2)
В пространстве параметров W Х решающая граница (граница разбиений между областями, относящимися соответственно к классу w i и классу w j) определяется условием di (X) = dj (X). Выражение для решающей границы и критерия (4.2) осуществляет классификацию параметров модели.
|
|
|
При определении области неопределенности для характеристики заданного класса параметров, необходимо определить полное расстояние между классами. Поскольку в рассматриваемом случае идентификация признаков производится последовательно, то при их идентификации важен порядок, в котором исследуются признаки, то есть признаки должны быть расположены в таком порядке, чтобы контроль дал окончательное решение возможно раньше. Задача упорядочения признаков является специальной задачей для последовательного распознавания. При наличии двух и большего числа классов, цель выбора признаков состоит в выборе таких признаков, которые являются наиболее эффективными с точки зрения разделимости классов. Причем критерий разделимости классов не должен зависеть от системы координат, и в общем случае критерии разделимости двух классов можно представить в виде
c (w i, w j, хi,..., хn) = c (w i, w j; Хn),
где n случайных величин хi,..., хn используются в качестве признаков.
Критерии разделимости двух классов должны удовлетворять следующим требованиям:
– монотонности связи с вероятностью ошибки, монотонности связи с верхней и нижней границами вероятности ошибки;
– инвариантности относительно взаимно однозначных отображений;
– аддитивности по отношению к независимым признакам, то есть если хn взаимно независимы, то c (w i, w j; Хn) =  (w i, w j; хk).
(w i, w j; хk).
Общий критерий разделимости классов формулируется с использованием как параметра рассеяния внутри классов, так и параметра рассеяния между классами. Он должен увеличиваться при увеличении расстояния между классами и при уменьшении рассеяния внутри классов.
В качестве разделяющей функции, наиболее полно удовлетворяющей данным требованиям, целесообразно использовать функцию правдоподобия, которая определяет вероятность принадлежности параметра Х данному классу w i. Так, после контроля n -го признака вычисляется разделяющая функция в виде функции правдоподобия [2, 113]
|
|
|
l n = 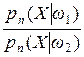
или в ее логарифмическом виде
l n 0 = ln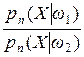 ,
,
где pn (X |w i), i = 1, 2 – n – мерная функция условной плотности вероятности X для класса образов w i. Далее функция l n 0 сравнивается с двумя останавливающими границами (порогами) А и B.
Если
l n 0 ³ А, (4.3)
то принимаемое решение X принадлежит классу w1, и если
l n 0 £ B, (4.4)
то принимаемое решение X принадлежит классу w2.
Если B <l n 0< А, то должен быть произведен дополнительный контроль, а процесс продолжается до (n + 1) – го шага. Значения A и В связаны с вероятностями ошибок ложного распознавания следующим образом [119]:
A = ln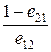 и B = ln
и B = ln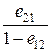 ,
,
где eij – вероятность принятия гипотезы Х, принадлежащей w i, когда в действительности истинной является гипотеза Х, принадлежащая w j, i, j = 1, 2.
Для двух классов образов классификатор, использующий последовательный критерий максимального правдоподобия, обладает оптимальными свойствами. При заданных величинах e 12 и e 21 не существует другой процедуры, которая обладала бы меньшими значениями риска и давала бы выигрыш в среднем числе контроля признаков по сравнению с последовательной процедурой классификации [113].
Выражения (4.3) и (4.4) при знаках равенства представляют собой решающие границы, которые разбивают пространство признаков на три области: область, относящуюся к классу w1; область, относящуюся к классу w2; область неопределенности, заключенную между границами и соответствующую условиям, когда не принято окончательное условие. Для последовательного процесса классификации решающие границы изменяются с числом замеров признаков n.
Параметр рассеяния внутри классов показывает разброс объектов относительно векторов математических ожиданий 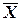 классов, в связи с этим в качестве критерия, характеризующего рассеяния внутри класса w i, целесообразно использовать функционал риска:
классов, в связи с этим в качестве критерия, характеризующего рассеяния внутри класса w i, целесообразно использовать функционал риска:
R (w i) = 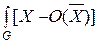 2 p (X |w i) dX, (4.5)
2 p (X |w i) dX, (4.5)
где O ( ) – оценка математического ожидания
) – оценка математического ожидания 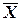 .
.
Параметр рассеяния между классами может быть определен несколькими способами, но все эти параметры рассеяния должны быть инвариантны относительно сдвига системы координат. Для выбора параметра рассеяния между классами учтем, что при распознавании образов одной из ключевых характеристик является отношение правдоподобия или – ln{ P (X |w1)/ P (X |w2)}, где P (X |w1) и P (X |w2) – плотности вероятностей классов w1 и w2. Поэтому, если есть возможность оценить плотности или функции распределения вероятностей для классов w1 и w2, это было бы почти эквивалентно оцениванию вероятностей ошибки. Простейший подход заключается в том, чтобы использовать математическое ожидание отношения правдоподобия для классов w1 и w2 и оценивать разделимость классов по разности математических ожиданий. Определенная данным образом разделимость классов сводится к функционалу дивергенции, который определяется следующим образом [114]:
|
|
|
D = 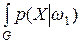 ln
ln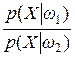 dX –
dX – 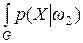 ln
ln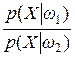 dX. (4.6)
dX. (4.6)
Определенные выражениями (4.5) и (4.6) параметры рассеяния позволяют составить общий критерий разделимости классов в виде
I = 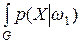 ln
ln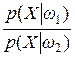 dX –
dX – 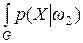 ln
ln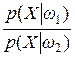 dX +
dX +
+ 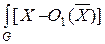 2 p (X |w1) dX –
2 p (X |w1) dX –  2 p (X |w2) dX.
2 p (X |w2) dX.
Минимум предлагаемого критерия разделимости классов определяется с помощью метода множителей Лагранжа и имеет вид [3]:
I min = R min(w1) +1 – 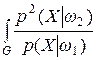 dX + R min(w2),
dX + R min(w2),
где R min(w i) – минимальный риск каждого из классов параметров.
На основании априорных данных, полученных в результате проведенного анализа идентифицируемого процесса, находятся решающие границы между классами и область неопределенности, для возможной корректировки алфавита классов и словаря признаков. При этом появляется возможность составления плана дискриминирующего эксперимента, то есть эксперимента по проверке конкретной статистической гипотезы о модели идентифицируемого процесса, а также отсеивающего эксперимента, задача которого состоит в выделении значимых факторов. По результатам, полученным в данных экспериментах, принимается решение об уточнении модели идентифицируемого процесса.
Выбор признаков датчика при пересекающихся областях их задания. Как показано в разд. 3.2, при постановке задачи формирования модели контроля, для конструирования пространства определения модели, необходимо обеспечить, возможно, простое разделение ее переменных как образов данного пространства. Составляющими этого пространства являются свойства датчика, называемые признаками, которые определяют особенности его выходной информации об оцениваемом параметре. Остальные свойства объекта исключаются из процесса распознавания, так как они несут информацию только об объекте, но не об оцениваемом параметре.
|
|
|
При формировании математической модели данного вопроса будем исходить из предположения [3], что на некотором множестве V определены подмножества V 1*,..., Vm *, представляющие собой образы на обучающей последовательности V= V 1*È V 2*È...È Vm *. При этом любое бинарное свойство разделит множество V на два подмножества V 1 i и V 2 i, все элементы одного из которых будут обладать этим свойством, а все элементы другого этим свойством обладать не будут. Тогда признаками следует считать только свойства xi 1, порождающие подмножества Vki (k = 1, 2), такие, что среди образов Vj * найдется такой, который обладает либо свойством
Vj Í Vki, (4.7)
либо свойством
Vki Í Vj *, (4.8)
где для любого k = 1, 2 Vki ¹ V.
Соотношения (4.7) и (4.8) определяют признаки соответственно первого и второго типа относительно Vj *.
Поскольку для датчика контроля характерны не бинарные, а непрерывные свойства, то признаками следует считать такие из них, на непрерывной шкале которых можно установить порог, обеспечивающий какое-либо из соотношений (4.7, 4.8):
xi = 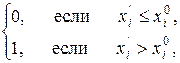 (4.9)
(4.9)
где xi ¢ – непрерывный контроль i – го свойства.
В пространстве признаков (определенных формулами (4.7) и (4.8)) в соответствии с фундаментальной теоремой Вапника–Червоненкиса [42] с вероятностью 1–h, можно достигнуть с вероятностью e линейного разделения образов, заданных обучающей последовательностью l. Причем, если соотношения (4.7) и (4.9) не выполняются ни при каких порогах, то данное разделение образов в непрерывном пространстве все же достижимо. Поэтому непрерывные свойства должны обладать более тонкими особенностями (чем соотношения (4.7), (4.8), (4.9)), чтобы называться признаками. Для выяснения этих особенностей рассмотрим плоскость, определяемую некоторыми непрерывными свойствами xi и xv распознаваемых объектов. На этой плоскости любая линейная функция вида [52]
F (x) = a 0 + a 1 xi + a 2 xv (4.10)
разделит обучающую последовательность на два подмножества V 1( i , v ) и V 2( i , v ) так, что для определенным образом зафиксированного k = 1, 2 получим
x Î Vk ( i , v ), если F (x) ³ 0; (4.11а)
x Î V k (i, v), если F (x) < 0. (4.11б)
Для этого коэффициенты a 0, a 1, a 2 должны подобраться так, чтобы обеспечивать
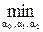 (Vk Ç V
(Vk Ç V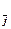 *) при Vj * Ì Vk, (4.12)
*) при Vj * Ì Vk, (4.12)
или
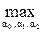 (Vk Ç Vj *) при Vk Ì Vj *, (4.13)
(Vk Ç Vj *) при Vk Ì Vj *, (4.13)
где k = 1, 2 соответствует номеру подмножеств, определяемых плоскостью (4.11), а 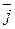 – индекс альтернативный j, если рассматривается Vj *, то V
– индекс альтернативный j, если рассматривается Vj *, то V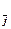 * – это множество всех образов за исключением Vj *, то есть V
* – это множество всех образов за исключением Vj *, то есть V 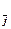 * = V \ Vj *. Тогда непрерывным признаком при заданной длине обучающей последовательности l и при заданных e и h будем считать каждую пару непрерывных свойств x i и xv, на плоскости которой можно построить такую линейную разделяющую функцию (4.10). Данная функция после оптимизации коэффициентов a 0, a 1, a 2 удовлетворила бы одному из условий (4.12) или (4.13). При этом непрерывные признаки первого типа определяются соотношением (4.12), а второго – соотношением (4.13).
* = V \ Vj *. Тогда непрерывным признаком при заданной длине обучающей последовательности l и при заданных e и h будем считать каждую пару непрерывных свойств x i и xv, на плоскости которой можно построить такую линейную разделяющую функцию (4.10). Данная функция после оптимизации коэффициентов a 0, a 1, a 2 удовлетворила бы одному из условий (4.12) или (4.13). При этом непрерывные признаки первого типа определяются соотношением (4.12), а второго – соотношением (4.13).
Чтобы обеспечить выполнение условий (4.12), (4.13) для исходных признаков, возможно введение дополнительного признака. Для оценки дополнительного признака определим количество дополнительной информации, которой обладает вводимое в виде признака свойство. Если Hi, i – 1, 2, – гипотеза о том, что X принадлежит статистической популяции с плотностью вероятности fi, то из теоремы Байеса следует, что
P (Hi | x) =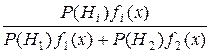 ,
,
откуда получаем
log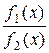 = log
= log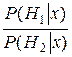 – log
– log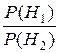 , (4.14)
, (4.14)
где P (Hi), i =1, 2–априорная вероятность Hi, а P (Hi | x)–апостериорная, или условная, вероятность Hi при условии, что X = x. Основание логарифма в данном выражении несущественно и определяет лишь единицу измерения.
Правая часть равенства (4.14) является разностью между логарифмами шансов в пользу H 1 до и после наблюдения X = x. Эту разность и можно рассматривать как информацию, получаемую в результате введения нового признака X = x, а логарифм отношения правдоподобия log[ f 1(x)/ f 2(x)] определяет информацию в точке X = x для различения в пользу вероятности H 1 против H 2.
С другой стороны, минимум введенного в работе [82] критерия разделимости классов признаков имеет вид
I min = R min(xi) +1 – 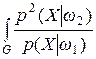 dX + R min(xv),
dX + R min(xv),
где R min(xi) – минимальный риск каждого из классов параметров. Из данного выражения следует, что зона неопределенности между классами определяется неопределенностью самих классов, то есть минимальными для данного класса рисками R min(xi). Таким образом, возможна ситуация, что ни одно из свойств xi и xv не является “чистым” признаком, и в плоскости, определяемой этими свойствами, образы неразличимы. При этом может существовать такое третье свойство xk, которое вместе со свойствами xi и xv, при соответствующем подборе коэффициентов a 0, a 1, a 2, a 3, приводит к линейному разделению образов плоскости F (x)= a 0+ a 1 xi + a 2 xv + a 3 xk. Введение в классификацию признаков очередного признака хk может повлиять на зону неопределенности при условии, что, например,
log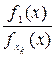 = R min(xk) + R min(xv)
= R min(xk) + R min(xv)
или
fxk = fxi exp{– [ R min(xk) + R min(xv)]},
причем плотность распределения fxk дополнительного признака должна удовлетворять общеизвестным требованиям нормировки. Полученное выражение для плотности распределения fxk порождает экспоненциальное семейство распределений, то есть семейство экспоненциального типа, определяемого посредством (данном случае) распределения fxi. В данном выражении может быть использовано в качестве порождающей плотности распределения и fxv. В более общем случае, при определении плотности распределения нового признака, необходимо учитывать тот факт, что данный признак не только должен “покрывать” неопределенность других признаков, но и обеспечивать дополнительный эффект распознавания, путем использования оставшихся слагаемых выражения для минимума критерия разделимости классов. Аналогично можно получить подобные результаты и для подпространств (совокупностей) более высокой размерности. Данный подход формирования модели исследуемого датчика можно рассматривать как синтез нового признака модели на базе известных признаков, не достаточных для обеспечения необходимого значения риска данной модели.
Введение в процесс контроля дополнительных факторов (комплексирование), коррелированных с выходной переменной, изменяет величину риска, дает возможность с большей точностью определять выходную переменную, так как уменьшается ее риск. Данный эффект объясняется эффектом эмерджентности (теорема 3.4.2) новой переменной, которая определяется, например, двумя независимыми исходными переменными.
Способ декоррелирования переменных модели. Для снижения риска результатов оценивания, в предыдущем методе синтезировалась новая переменная, которая вследствие эффекта эмерджентности обладает дополнительной информацией об оцениваемом параметре объекта. При оценивании параметра объекта по результатам контроля нередко возникает ситуация, когда области определения заданных переменных ММК имеет общую область пересечения, то есть данные переменные нельзя отнести к классу независимых переменных. При этом оценки этих переменных характеризуются неоднозначностью их определения, что приводит к снижению качества оценки результатов контроля, поскольку увеличивается риск оценивания.
Устранение неоднозначности при формировании и тем самым снижение риска при оценке результатов контроля можно достигнуть путем априорного изменения условий проведения эксперимента, трансформируя переменные модели контроля. Для получения условий преобразования переменных ММК при оценке результатов контроля с общей областью пересечения переменных, рассмотрим следующую постановку задачи формирования ММК [81].
Пусть план эксперимента x N = { x 1,..., xn; p 1,..., pn }, где pi = 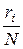 , точки xi – опорные точки плана, а величины pi – меры этих точек (веса). Дисперсионная матрица оценок определяется планом эксперимента:
, точки xi – опорные точки плана, а величины pi – меры этих точек (веса). Дисперсионная матрица оценок определяется планом эксперимента:
D [x N ] = N –1M–1(x N) = N –1 D (x N),
где M(x N) – (нормированная) информационная матрица, D (x N)=M–1(x N).
В силу предположения о некоррелированности погрешностей e ij:
M(x N) = 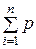 i m(xi),
i m(xi),
где m(xi)–прирост информационной матрицы от одного наблюдения в точке xi.
Для оптимизации эксперимента решают экстремальную задачу:
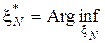 Ф[ N M(x N)].
Ф[ N M(x N)].
При этом матрица M(x N), а стало быть и матрица D (x N) определяют оптимальные априорные планы и минимизируют некоторую заданную функцию от матрицы N M(x N), а функция Ф[ N M(x N)] является критерием оптимальности. Рассмотрение функций от матрицы N M(x N), а не от матрицы D (x N) удобнее, так как позволяет охватить случаи не только регулярных планов, когда rgM(x N)= m, но и сингулярных планов, в которых rgM(x N)< m, но Ф[ N M(x N)]>0. При формировании новых переменных эксперимента целесообразно использовать дисперсионную матрицу оценок:
Dn (xi) = 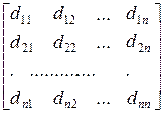 ,
,
где dij = E [ xixj T] (i, j = 1, 2,..., n).
Введенная модель эксперимента, а также свойство симметричности, используемое для характеристики эксперимента информационной и дисперсионной матриц, позволяют формально решить задачу преобразования исходной матрицы к диагональному виду. Получить диагональную матрицу 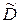 n (xi) из исходной Dn (xi) можно путем транспозиции ее строк и столбцов [67]. Если в матрице Dn (xi) есть элементы, отличные от нуля, то транспозицией строк и столбцов добиваются, чтобы элемент d 11 был отличен от нуля. Умножив затем первую строку на
n (xi) из исходной Dn (xi) можно путем транспозиции ее строк и столбцов [67]. Если в матрице Dn (xi) есть элементы, отличные от нуля, то транспозицией строк и столбцов добиваются, чтобы элемент d 11 был отличен от нуля. Умножив затем первую строку на 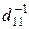 , можно преобразовать элемент d 11 в единицу. Если вычесть теперь из j – го столбца (j >1) первый столбец, умноженный на d 1 j, то d 1 j будет заменен нулем. Делая эти преобразования со всеми столбцами, начиная со второго, а также со всеми строками, получают
, можно преобразовать элемент d 11 в единицу. Если вычесть теперь из j – го столбца (j >1) первый столбец, умноженный на d 1 j, то d 1 j будет заменен нулем. Делая эти преобразования со всеми столбцами, начиная со второго, а также со всеми строками, получают 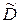 n (xi).
n (xi).
Для получения выражения преобразования переменных ММК воспользуемся теоремой [62], в соответствии с которой для любой действительной симметричной матрицы D можно определить действительную невырожденную матрицу T, для которой матрица 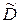 = T T DT диагональна, все собственные значения которой действительны, а размерность собственного пространства, принадлежащего собственному значению l, совпадает с кратностью l. Получение диагональной дисперсионной матрицы эксперимента означает, что в новом эксперименте, который адекватен исходному, используются новые некоррелированные между собой переменные.
= T T DT диагональна, все собственные значения которой действительны, а размерность собственного пространства, принадлежащего собственному значению l, совпадает с кратностью l. Получение диагональной дисперсионной матрицы эксперимента означает, что в новом эксперименте, который адекватен исходному, используются новые некоррелированные между собой переменные.
Матрица 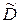 2(xi), полученная по данному алгоритму в работе [81], определяет новую модель эксперимента, для которой характерно некоррелированность переменных, а в случае если ее переменные характеризуются нормальным законом распределения, то и независимостью. Проведенные формальные преобразования матрицы D 2(xi) в диагональную матрицу
2(xi), полученная по данному алгоритму в работе [81], определяет новую модель эксперимента, для которой характерно некоррелированность переменных, а в случае если ее переменные характеризуются нормальным законом распределения, то и независимостью. Проведенные формальные преобразования матрицы D 2(xi) в диагональную матрицу 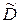 2(xi) преобразовывают переменные модели эксперимента путем поворота оси координат на угол
2(xi) преобразовывают переменные модели эксперимента путем поворота оси координат на угол
j1 = arctg 
или
j2 = arctg  .
.
При этом проекции областей определения полученных переменных модели эксперимента на оси новой системы координат не имеют области пересечения.
Ограничением применения рассмотренного способа снижения неопределенности при оценивании параметров объекта является вырожденность исходной информационной матрицы, что приведет к невозможности определения обратной к ней дисперсионной матрицы. Использование данного подхода при трансформации переменных невозможно и приходится пользоваться другими вышерассмотренными методами формирования ММК.
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 342; Нарушение авторских прав?; Мы поможем в написании вашей работы!