
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Понятие и виды средних величин, способы их вычисления
|
|
|
|
Тема 5.2 Средние величины в статистике.
Чтобы определить значение признака характерного для всей совокупности единиц прибегают к расчету средних величин. Средней величиной называются показатели, которые выражают типичные черты и дают обобщенную количественную характеристику признаков данного явление.
Средние величины исчисляются только в однородных совокупностях. При исчислении в неоднородных совокупностях необходимо эту совокупность расчленить на однородные, а затем производить вычисления средней величины.
Различают следующие виды средних величин:
1. Средняя арифметическая
2. Средняя гармоническая
3. Средняя геометрическая
4. Средняя степенная (квадратичная, кубическая и т.д.).
Помимо степенных средних в статистике используются структурные средние: мода и медиана. Средние - арифметические бывают: простой и взвешенной,
Простая используется, когда первичные данные не систематизированы и вычисляется как сумма индивидуальных значений признака, деленная на их количество.
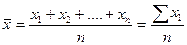

где 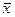 - средние значения признака, n - количество индивидуальных значений,
- средние значения признака, n - количество индивидуальных значений,
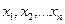
 - индивидуальные значения признаков.
- индивидуальные значения признаков.
Пример 1. Пять торговых центров фирмы имеют следующий объём товарооборота за месяц:
| Экономический показатель | Торговый центр (i) | ||||
Товарооборот, млн., рублей 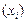
|
Решение:




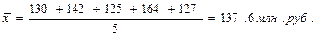
т.е. использована формула средней арифметической простой.
В случае, когда данные совокупности сгруппированы в виде вариационного ряда, используется средняя арифметическая взвешенная.
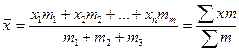
где m - частоты повторения одинаковых признаков, (весы признака).
Пример 2. Результаты торгов акциями АО:
|
|
|
| Сделка | Количество проданных акций, штук (т,) | Курс продажи, рубли (х,) |
| (mi) 500 | (xi) 1080 | |
Решение:
Используем формулу средней арифметической взвешенной
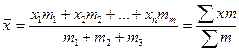
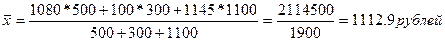
т.е. определена средняя величина - курс продажи акций. _
Средняя гармоническая, вычисляется тогда, когда в качестве исходной информации используются данные, характеризующие индивидуальные значения и объем признака. Она, может быть, простой и взвешенной.
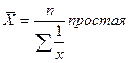
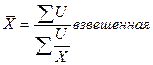
где, n - число значений признака (х), из которых исчисляется средняя;
U - объем признака (выступает в качестве весов индивидуальных значений признака х);
Х - числовое значение признака.
Пример 3. Один работник тратит на операцию по обработке корреспонденции 1,5 минут, а другой - 1 минуту. Найти средние затраты времени на эту операцию при условии, что оба работника были заняты 7 часов. Решение:
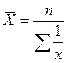
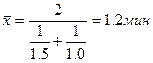
Используем формулу средней гармонической простой т.е. средняя продолжительность операции составила 1,2 минуты.
Пример 4. Валовой сбор и урожайность подсолнечника по Центрально-Чернозёмному району (в хозяйствах всех категорий).
| Область |  Валовый сбор, тыс. тонн Валовый сбор, тыс. тонн
| 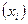 Урожайность, ц/га Урожайность, ц/га
|
| Белгородская | 97,0 | 16,1 |
| Воронежская | 204,0 | 9,5 |
| Курская | 0,5 | 4,8 |
| Липецкая | 16,0 | 10,9 |
| Тамбовская | 69,0 | 7,0 |
Необходимо определить среднюю урожайность подсолнечника во всех областях.
Решение:
Используем формулу средней гармонической взвешенной.
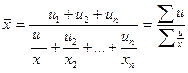

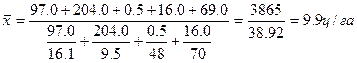
т.е. средняя урожайность - 9,9ц с одного гектара.
Средняя геометрическая исчисляется из ежегодных темпов роста.
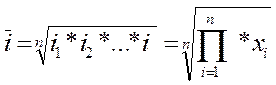
где, i — ежегодные темпы роста, n - количество ежегодных темпов роста.
Средняя Квадратичная.
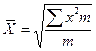
где, х - числовое значение признака, m- частоты признака.
«Статистика», под редакцией В.С.Мхитаряна
|
|
|
Учебник для студентов среднего профессионального образования,
М., ИЦ «Академия», 2007 г. стр. 101 - 112
Тема 5.3. Показатели вариации в статистике.
Вариация представляет собой изменение значений, какого - либо признака или его колеблемости за определенный период времени, или на момент времени. Показатели, характеризующие, колеблемость признаков получили название - показатели вариации.
1. Размах вариации – это абсолютная разность между Xmax и Xmin значениями признака
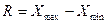
2. Среднее линейное отклонение – определяется из отклонений индивидуальных значений признака от средней величины.
Среднее линейное отклонение определяется по следующим формулам:
Для ранжированного ряда для интервального рада
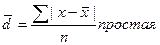
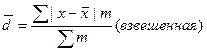
где, х – значение варьирующего признака;
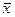 – средняя арифметическая величена;
– средняя арифметическая величена;
m – частота отдельных вариантов
3. Дисперсия признака, а квадратный корень из дисперсии – это среднее квадратичное отклонение. Оба этих показателя определяются по формулам:
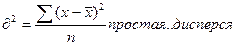
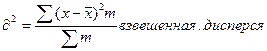
4. Корень квадратный из дисперсии  представляет собой средне квадратичное отклонение:
представляет собой средне квадратичное отклонение:
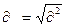
Среднее квадратичное отклонение 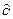 определяется по формулам:
определяется по формулам:
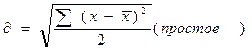
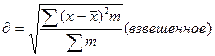
Чтобы сравнить степень колеблемости различных совокупностей, вычисляют относительные показатели вариации.
Коэффициент вариации представляет отношение среднего квадратического отклонения к средней арифметической.
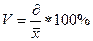
Пример 6. Для изучения естественной убыли произведено 5% -ное выборочное обследование партии хранящихся на базе товаров. В результате лабораторного анализа установлено следующее распределение образцов:
| Процент естественной убыли (X) | Количество образцов (т) |
| До4 | |
| 4-6 | |
| 6-8 | |
| 8-10 | |
| От 10 и выше | |
| итого |
Решение:
Середина интервала определяется
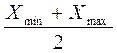 , т.е.
, т.е.
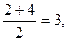
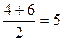 ,
, 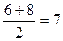 ,
, 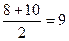 ,
, 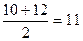 .
.
Расчёты для средней величины, дисперсии признака произведём в таблице. Расчётная таблица:
| Процент естественной убыли | Кол-во образцов (m) | Середина интервала (x) | х*m | 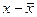
| 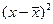
| 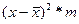
|
| До4 | -5 | |||||
| 4-6 | -3 | |||||
| 6-8 | -1 | |||||
| 8-10 | +1 | |||||
| От 10 и выше | +3 | |||||
| Итого | - | - | - |
|
|
|
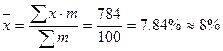
Средний процент естественной убыли в выборочной совокупности.
Дисперсия признака:
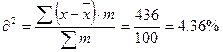
Среднее квадратичное отклонение:
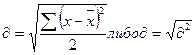
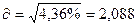
Коэффициент вариации:
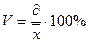
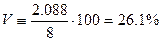
«Статистика», под редакцией В.С.Мхитаряна
Учебник для студентов среднего профессионального образования,
М., ИЦ «Академия», 2007 г. стр. 116-119
Тема 5.4. Структурные характеристики вариационного ряда распределения.
Структурные средние применяются для изучения внутреннего строения и структуры рядов распределения значения признаков, к таким показателям относятся мода и медиана.
Мода - это такая величина признака, которая в данном вариационном ряду встречается наиболее часто. В интервальном ряду мода исчисляется по формуле:
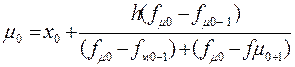
Где, х0 – нижняя граница модального интервала (модельным называется интервал, имеющий наибольшую частоту);
h – ширина модального интервала;
f μ 0 – частота модального интервала;
f μ 0-1 – частота интервала, предшествующего модальному;
f μ 0+1 – частота интервала, следующего за модальным.
Расчет моды, как средней величины применяется при хаотичном расположении ряда, который невозможен, подвергнуть к группировке.
Медиана — это величина признака, находящаяся в середине ряда, т.е. делящая ряд пополам.
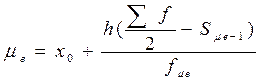
где, х0 – нижняя граница медианного интервала (медианным называется первый интервал, накопленная частота которого превышает половину общей суммы частот);
h – ширина модального интервала;
S μ e-1 - накопленная частота интервала, предыдущего медианному;
∑f – сумма частот или число членов ряда;
f μе – частота медианного интервала.
Для определения медианного значения признака по следующей формуле находят номер медианной единицы ряда:
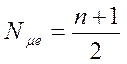
где, n – объём совокупности.
Пример 5. Распределение населения РФ по уровню среднедушевых денежных доходов за год.
| Среднедушевой денежный доход (в среднем за месяц), руб. | Численность населения, млн. человек |
| до 400 | 22,1 |
| 400-600 | 27,8 |
| 600-800 | 25,2 |
| 800-1000 | 19,6 |
| 1000-1200 | 14,3 |
| 1200-1600 | 17,6 |
| 1600-2000 | 9.0 |
| 2000 и более | 11,1 |
| Итого | 146,7 |
|
|
|
Интервал с границами 400-600 в данном распределении будет модальным, так как он имеет наибольшую частоту. Используя формулу определим моду.
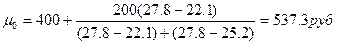
Для определения медианного интервала необходимо рассчитывать накопленную частоту каждого последующего интервала до тех пор, пока она не превысит 1/2 суммы накопленных частот (в нашем случае- 73,35- 146/2). Таким образом, медианным является интервал с границами 600-800. Тогда медиана равна:
| Интервал | Накопленная частота, млн. человек |
| До 400 | 22,1 |
| 400-600 | 49,9 |
| 600-800 | 75,1 |
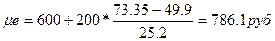
Если Хср, Me, Mo совпадают, то данная группа симметрична. Но Ме < Хср при немногочисленной группе с очень высокими числами и Хср < Ме, если нет очень больших чмсел и данные концентрируются.
Если совокупность неоднородна, то мода трудно определяется. Мо < Хср, если имеется немногочисленная группа с высокими числами и Мо отчетливо выражена при однородности группы.
Контрольные вопросы
1. Дать определение средней величины.
2. Перечислить виды средних.
3. Напишите формулы:
- средней арифметической простой и взвешенной;
- средней геометрической простой и взвешенной.
4. Для каких целей используется формула средней геометрической?
5. Что такое мода и медиана? Методика их расчёта.
6. Для каких целей изучается вариация? Способы расчёта показателей вариации.
7. Дисперсия, виды дисперсии, методы их расчёта.
8. Что показывает коэффициент вариации? Как он определяется?
«Статистика», под редакцией В.С.Мхитаряна
Учебник для студентов среднего профессионального образования,
М., ИЦ «Академия», 2007 г. стр. 112- 116
Раздел 6. Ряды динамики в статистике
|
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 6349; Нарушение авторских прав?; Мы поможем в написании вашей работы!