Лекция 4. Метод включения и исключения. Формула решета

Пусть дано n -множество элементов S и N- множество свойств p ₁,…, p_N. Элементы множества S могут как обладать, так и не обладать любым из свойств p_i. Количество элементов, обладающих теми или иными свойствами и их комбинациями, известно.

Требуется найти число элементов, не обладающих ни одним из свойств.

Обозначим:

1) через 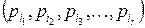некоторую i -ю выборку свойств, а через 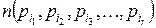– число элементов, каждый из которых обладает всеми этими r выбранными свойствами.

2) через 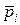– отсутствие у элемента свойства p_i. Тогда, например, 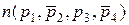– число элементов, обладающих свойствами p ₁ и p₃ и не обладающих свойствами p₂ и p₄.

Рассмотрим два частных случая.

1. Имеется лишь одно свойство p. Тогда очевидно, что число элементов, не обладающих свойством p, равно общему числу элементов минус число элементов, обладающих свойством p. .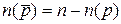

2. Имеется конечное множество свойств p ₁,…, p_N, но они не совместимы (т.е. ни один из элементов не может обладать более чем одним свойством). Тогда число элементов, не обладающих ни одним из свойств, равно общему числу элементов минус число элементов, обладающих свойством p ₁, минус число элементов, обладающих свойством p ₂ и т.д.

.

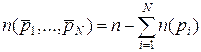Общий случай – элементы могут обладать комбинацией совместимых свойств.

Теорема. Если даны n -множество элементов S и N свойств p_i 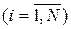, то число элементов, не обладающих ни одним из свойств, равно (формула решета):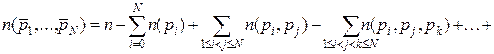

.

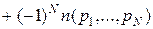n n (p ₁) n (p₂)     n (p₃)

# Рассмотрим доказательство при N =3.

Обозначим кругами подмножества элементов, обладающих хотя бы свойством p ₁, хотя бы свойством p ₂ и хотя бы свойством p ₃. Тогда пересечения двух кругов будут давать подмножество элементов, обладающих хотя бы двумя свойствами одновременно, а пересечение всех трех кругов дает подмножество элементов, обладающих всеми тремя свойствами. Прямоугольник, в котором расположены круги, обозначает все множество S, содержащее n элементов. Нужно найти количество элементов, не обладающие ни одним из трёх свойств (за пределами кругов).

Чтобы найти это число, нужно из n -множества исключить элементы, обладающие свойством p ₁, затем обладающие свойством p₂, затем – p₃, т.е. вычесть 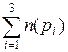. Однако при этом элементы, обладающие двумя свойствами (например, p ₁ и p₂), окажутся исключёнными дважды (сначала как элементы, обладающие свойством p ₁, затем как обладающие p₂). Следовательно, нужно возвратить по одному разу элементы, исключённые дважды, т.е. добавить 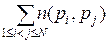. Но при этом элементы, обладающие сразу тремя свойствами (p ₁, p₂, p₃), сначала были трижды исключены как элементы, обладающие по отдельности свойствами p ₁, p₂ или p₃, а затем трижды включены как обладающие парами свойств. Поэтому их нужно один раз исключить, т.е. вычесть 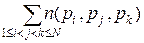. Рассуждая подобным образом, получаем алгоритм, который состоит в попеременном включении и отбрасывании подмножеств, дающий приведенную выше формулу решета. #

Следствие. Характер доказательства таков, что его можно применять к любой комбинации свойств. Например,

.

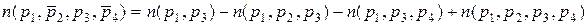Примечание 1. Символическая запись метода:

, (*)

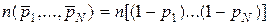где буквой n обозначен функциональный знак. Смысл такой записи – сначала раскрываем круглые скобки внутри квадратных, а затем знак функции n приписываем к каждому из слагаемых. Например,

,

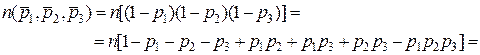
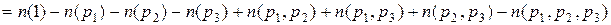считая, что .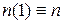

Примечание 2. В теории вероятности формула (*) называется теоремой Пуанкаре – вычисление вероятности ненаступления одновременно нескольких событий, зная вероятность наступления каждого.

Теорема. .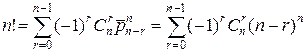

# Рассмотрим множество из n элементов. Из них можно образовать 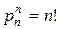перестановок без повторений и 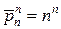перестановок с повторениями. Ясно, что 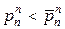при n >1 (перестановки без повторений – подмножество перестановок с повторениями).

Если в n -выборке один и тот же элемент x_j встречается хотя бы два раза, то значит, что какого-то другого элемента x_i в ней нет. Определим свойство p_i – «в выборке нет элемента x_i». Тогда n (p_i) – число выборок, в которых нет хотя бы элемента x_i, n (p_i,p_j) – число выборок, в которых нет хотя бы x_i и x_j (i ¹ j). И т.д.

Перестановки по n элементов из n без повторений – это выборки, в которых присутствуют все n элементов, т.е. их число .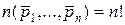

По теореме включения и исключения:

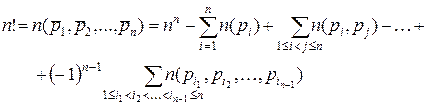
(последнее слагаемое – число выборок, составленных из 1 элемента, а остальных (n -1) в них нет; например, 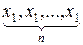или ).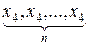

Один элемент можно выбрать 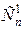способами, при этом выборки, где его нет, это n ‑выборки с повторениями из (n -1) элементов, число которых равно 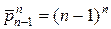. Значит, всего выборок, где нет хотя бы одного элемента, .

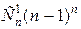Два элемента можно выбрать 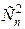способами, а выборки, где их нет – это n ‑выборки с повторениями из (n -2) элементов, число которых равно 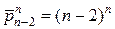. Значит, всего выборок, где нет хотя бы двух элемента, .

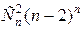Аналогично получаем количества выборок, в которых нет хотя бы 3-х элементов, 4-х, и т.д., …, (n -1) элемента. Подставляем в формулу решета:

. #

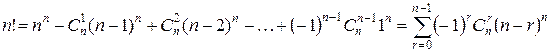Проверим:

,

,

.

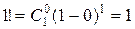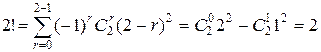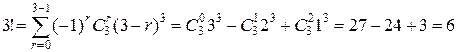Лекция 5. Задача о беспорядках

Пусть имеется конечное упорядоченное множество элементов {1,…, n }. Из этих элементов могут быть образованы перестановки a ₁,…, a_n (a_i Î{1,…, n }). Число всех возможных перестановок – n!. Среди этих n! перестановок есть такие, что ни один элемент не стоит на своём месте (a_i ¹ i, i =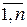). Иначе говоря, элемент номер 1 не стоит на 1-ом месте, элемент номер 2 не стоит на 2-м месте, и т.д., элемент номер n не стоит на n -м месте. Такие перестановки называются беспорядками.

Число беспорядков из n элементов обозначается D_n (ясно, что D_n<n!).

Теорема. Число беспорядков из n элементов равно:

.

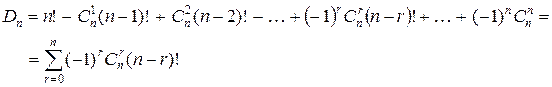# Обозначим через свойство p_i – «i -й элемент стоит на i -м месте». Тогда по формуле решета .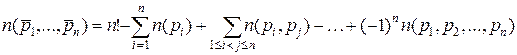

Общее число перестановок n элементов – n! Число перестановок, где i -й элемент стоит на i -м месте, равно (n -1)! (ставим i -й элемент на i -е место, а оставшиеся n -1 элементы переставляем (n -1)! способами). При этом сам i -й элемент можно выбрать 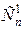способами. Таким образом, число перестановок, где хотя бы по одному элементу стоит на своём месте, равно .

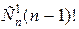Число перестановок, где i -й элемент стоит на i -м месте, а j -й на j -м (i ¹ j), равно (n -2)!, при этом i -й и j -й элементы можно выбрать 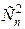способами. Таким образом, число перестановок, где хотя бы два элемента стоят на своих местах – .

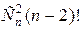Аналогично, число перестановок, где на своих местах стоят хотя бы три элемента – 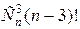. Число перестановок, где на своих местах стоят хотя бы r элементов – 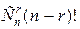. Число перестановок, где все элементы стоят на своих местах 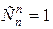. Подставляем в формулу решета: #

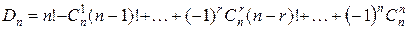Дата добавления: 2014-01-05