
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные понятия детерминированных конечных автоматов
|
|
|
|
Тема 5.2. Детерминированные конечные автоматы
Резюме по теме
Вопросы для повторения
1.Конечный автомат это?
2.В чем отличие конечного автомата и просто автомата?
3.Назовите множества, которые описывают конечный автомат?
4.Приведите различие модели автомата Мили и Мура?
5.Приведите способы задания автоматов?
6.Как осуществляется переход от автомата Мили к модели автомата Мура?
7. Как осуществляется переход от автомата Мура к модели автомата Мили?
8.Сформулируйте достоинства и недостатки различных способов задания автоматов?
9.Что такое функция переходов?
Показан способ принятия решений при помощи конечных автоматов. Даны основные характеристики и способы представления информации конечными автоматами. Выявлена структура автомата с его набором множеств, таких например, как множество входных и выходных значений. Рассмотрены способы задания автоматов. Приведены наиболее часто используемые автоматы Миля и Мура, а так же показано их отличие в работе. Рассмотрена взаимосвязь между моделями автоматов Миля и Мура, где показан переход из одной модели в другую и наоборот.
Цель: ознакомиться с детерминированными конечными автоматами.
Задачи:
1. Рассмотреть основные понятия детерминированных конечных автоматов.
2. Изучить схему доказательства правильности автомата.
3. Показать как осуществляется произведение автоматов.
Конечные автоматы часто используются для определения тех или иных свойств слов, т.е. для распознавания языков: автомат, распознающий некоторый язык L должен по произвольному слову w ответить на вопрос w  L?. Для решения такой задачи функция выходов может быть заменена на проверку того, в какое состояние переходит автомат после получения входного слова w принимающее или отвергающее.
L?. Для решения такой задачи функция выходов может быть заменена на проверку того, в какое состояние переходит автомат после получения входного слова w принимающее или отвергающее.
|
|
|
Детерминированный конечный автомат (ДКА) – распознаватель - это система вида
A =< Σ, Q, q0, F, Φ, >,
включающая следующие компоненты:
Σ = {a1,..., am} (m ≥ 1) конечное множество - входной алфавит;
Q = {q0,..., qn−1}(n ≥ 1) конечное множество - алфавит внутренних состояний;
q0  Q начальное состояние автомата;
Q начальное состояние автомата;
F  Q множество принимающих (допускающих, заключительных) состояний;
Q множество принимающих (допускающих, заключительных) состояний;
Φ: Q Ч Σ → Q функция переходов, Φ(q, a) это состояние, в которое переходит автомат из состояния q, когда получает на вход символ a.
Функцию Φ называют программой автомата A и задают как список из mn команд вида qiaj→Φ(qi, aj).
Удобно также задавать функцию Φ с помощью описанной выше таблицы размера n  m, строки которой соответствуют состояниям из Q, а столбцы символам из входного алфавита Σ, в которой на пересечении строки qi и столбца aj стоит состояние Φ(qi, aj).
m, строки которой соответствуют состояниям из Q, а столбцы символам из входного алфавита Σ, в которой на пересечении строки qi и столбца aj стоит состояние Φ(qi, aj).
Как и автоматы-преобразователи, автоматы-распознаватели можно представлять с помощью размеченных ориентированных графов, называемых диаграммами.
Диаграмма ДКА A =< Σ, Q, q0, Φ > это ориентированный мультиграф DA= (Q, E) с помеченными ребрами, в котором выделена вершина начальное состояние q0 из каждой вершины q  Q выходит |ΣX| ребер, помеченных символами a
Q выходит |ΣX| ребер, помеченных символами a  Σ так, что для каждой q
Σ так, что для каждой q  Q и каждого символа a
Q и каждого символа a  Σ имеется единственное ребро из q в вершину q0 = Φ(q, a) с меткой a.
Σ имеется единственное ребро из q в вершину q0 = Φ(q, a) с меткой a.
Скажем, что представленный последовательностью ребер путь p = e1e2... et в диаграмме несет слово w = w1w2... wt, если wi это метка ребра ei(1 ≥ i ≥ t). Если q начальная вершина (состояние) этого пути, а q’ его заключительная вершина, то будем говорить, что слово w переводит q в q’.
Работа конечного автомата-распознавателя состоит в чтении входного слова и изменению состояний в зависимости от его символов.
Конфигурация ДКА A =< Σ, Q, q0, F, Φ, > - это произвольная пара вида (q, w), в которой q  Q и w
Q и w  Σ∗ (напомним, что через Σ∗ обозначено множество всех слов в алфавите Σ, включающее и пустое слово ε).
Σ∗ (напомним, что через Σ∗ обозначено множество всех слов в алфавите Σ, включающее и пустое слово ε).
|
|
|
На множестве конфигураций введем отношение перехода за один шаг: ├А
(q, w) `A(q’, w’) 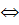 w = aw’, Φ(q, a) = q’.
w = aw’, Φ(q, a) = q’.
Если w = ε, то положим для каждого q  Q: (q, ε) ├А (q, ε).
Q: (q, ε) ├А (q, ε).
Через обозначим рефлексивное и транзитивное замыкание.
обозначим рефлексивное и транзитивное замыкание.
Содержательно, (q, w) 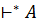 (q’, w’) означает, что автомат A, начав работу в состоянии q на слове w = w1... wl через некоторое конечное число шагов 0 ≤ k ≤ l прочтет первые k символов слова w и перейдет в состояние q’, а w’= wk+1... wl это непрочтенный остаток слова w.
(q’, w’) означает, что автомат A, начав работу в состоянии q на слове w = w1... wl через некоторое конечное число шагов 0 ≤ k ≤ l прочтет первые k символов слова w и перейдет в состояние q’, а w’= wk+1... wl это непрочтенный остаток слова w.
ДКА A распознает (допускает, принимает) слово w, если для некоторого q  F (q0, w)
F (q0, w) 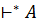 (q, ε), т.е. после обработки слова w автомат переходит в принимающее состояние.
(q, ε), т.е. после обработки слова w автомат переходит в принимающее состояние.
Язык LA, распознаваемый (допускаемый, принимаемый) автоматом A, состоит из всех слов, распознаваемых этим автоматом:
LA= {w | A распознает w}.
Язык называется, конечно автоматным, если он распознается некоторым ДКА.
Из этого определения, в частности, следует, что ε  LA
LA 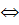 q0
q0  F. Один и тот же язык может распознаваться разными автоматами.
F. Один и тот же язык может распознаваться разными автоматами.
Автоматы A и B называются эквивалентными, если совпадают распознаваемые ими языки, т.е. LA= LB.
Определение распознавания слова и языка можно легко перевести на язык диаграмм.
Лемма 1. Автомат A распознает (допускает, принимает) слово w, если для некоторого q  F в диаграмме DA имеется путь из q0 в q, который несет слово w, т.е. w переводит q0 в заключительное состояние q.
F в диаграмме DA имеется путь из q0 в q, который несет слово w, т.е. w переводит q0 в заключительное состояние q.
Доказательство можно провести индукцией по длине слова w.
Таким образом, язык LA, распознаваемый автоматом A, состоит из всех слов, которые переводят в его диаграмме DA начальное состояние q0 в заключительные состояния из F.
Во многих случаях удается доказать, что язык L конечно автоматный, непосредственно построив распознающий его автомат. Для этого нужно постараться разбить множество всех входных слов на конечное число классов однородных, эквивалентных слов, т.е. слов, получение которых на входе одинаково влияет на возможность их продолжения до слов распознаваемого языка. Затем для каждого такого класса создать состояние автомата и определить переходы между этими состояниями. Часто полезно бывает выделить одно состояние для представления ошибочных слов, для которых ни они сами, ни любые их продолжения не входят в язык.
|
|
|
|
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 1576; Нарушение авторских прав?; Мы поможем в написании вашей работы!