Лекция №2. Плоские электромагнитные волны. Поляризация волн

Рассмотрим бесконечное трехмерное пространство, в котором отсутствуют свободные заряды r=0 и с заданными электродинамическими параметрами 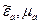, одинаковыми во всех точках. Гармонически изменяющийся электромагнитный процесс будет описываться системой уравнений Максвелла. Из уравнений (1.2)-(1.5), путем математических преобразований, выводится уравнения Гельмгольца:

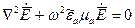. (2.1)

Уравнение (2.1) – однородное дифференциальное уравнение второго порядка. Для простоты решения введем параметр:

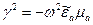(2.2)

и будем считать, что: 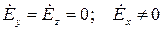. Кроме того, 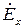зависит только от координаты z, то есть: 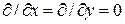. Тогда решение уравнения (2.1) будет:

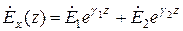, (2.3)

где 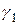и 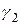корни уравнения (2.2). Распишем их:

,

.

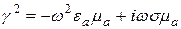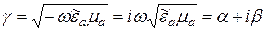Отсюда: 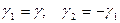, и выражение (2.3) запишется в виде:

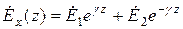. (2.4)

Выражение (2.4) – однородная плоская волна. Первое слагаемое – волна, распространяющаяся в сторону уменьшения z. Второе – в сторону увеличения. Отсюда величина g – коэффициент распространения.

Плоской называют волну, распространяющуюся вдоль какой-либо координаты и неизменную в каждый фиксированный момент времени в плоскости перпендикулярной этой координате:

.

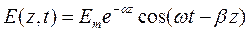Параметр b играет роль «пространственной» частоты процесса – коэффициент фазы (1/м). Её период: 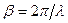, где l - длина волны.

Поверхность, удовлетворяющая условию: называется волновой фронт (фазовый фронт, поверхность равных фаз), перемещающийся вдоль оси z с фазовой скоростью:

.

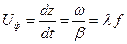Величина a – коэффициент ослабления плоской волны в среде (1/м).

В расчетах чаще используют погонное затухание:

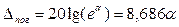дБ/м.

Используя второе уравнение Максвелла, найдем Н и подставим величину g:

.

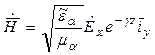Некоторые выводы:

– в однородной плоской волне векторы Е и Н перпендикулярны;

– и Е и Н перпендикулярны оси распространения – поперечная волна;

– комплексные амплитуды векторов Е и Н в любой точке пространства связаны коэффициентом пропорциональности Zc.

Zc - характеристическое (волновое) сопротивление:

.

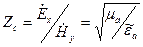Волновое сопротивление Zc характеризует среду и, в общем случае, не связано с тепловыми потерями.

Определим плотность потока мощности плоской ЭМВ:

,

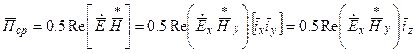или с учетом Zс:

.

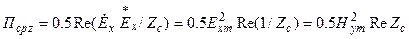Рассмотрим, как изменятся приведенные выше соотношения, если среда распространения – вакуум: .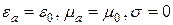

Коэффициент распространения: 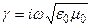чисто мнимый (потерь нет). Коэффициент фазы , тогда фазовая скорость 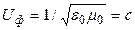не зависит от частоты.

Отсюда Z₀ – действительное, и равно 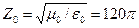Ом. Векторы Е и Н колеблются в фазе. Отметим, что для атмосферного воздуха это тоже справедливо.

В среде без потерь, но с e>1, m>1:

;

.

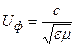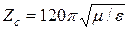На практике в СВЧ - диапазоне используют, как правило, диэлектрик с малыми потерями и m» 1. Для расчета основных характеристик плоских ЭМВ в этом случае используются следующие выражения:

,

.

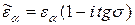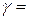
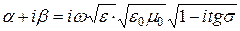Если tgs<<1, то есть, в случае малых потерь, 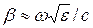, а a – прямо пропорционален w и s:

.

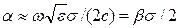Характеристическое сопротивление в этом случае:

.

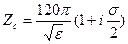Так как Zс – комплексная величина, то векторы Е и Н колеблются не синфазно и угол сдвига фаз приблизительно равен s/2.

В хорошо проводящих средах, даже при постоянстве m_а, абсолютная диэлектрическая проницаемость 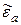является функцией частоты: 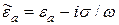, то есть наблюдается частотная дисперсия.

Говорят, что на заданной частоте wматериальная среда является хорошо проводящей (металлоподобной), если:

s¤w>>e_а, (2.5)

то есть плотность токов проводимости значительно превышает плотность токов смещения и поляризационных токов.

Как следствие на низких частотах неидеальные диэлектрики и полупроводники становятся металлоподобными (сухая почва при частоте f=1МГц ведет себя как хорошо проводящая среда). Но даже на самых высоких частотах радиодиапазона неравенство (2.5) выполняется для металлов с большим запасом.

В хорошо проводящей среде можно приближенно считать:

.

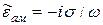Тогда .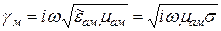

Используя выражение, 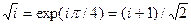перейдем к a и b:

.

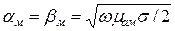Обе величины сильно зависят от w, дисперсия ярко выражена:

;

.

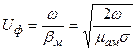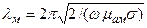Характеристическое сопротивление:

.

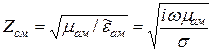Величина 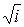означает, что в проводнике вектор Н сдвинут по фазе относительно вектора Е на 45°.

Если a ¹ 0, то амплитуда плоской ЭМВ изменяется вдоль координаты распространения Z по закону .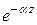

Расстояние, на котором амплитуда уменьшается в е раз, называют глубиной проникновения или толщиной поверхностного слоя (d):

;

.

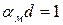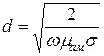На СВЧ диапазоне глубина проникновения очень мала. Для меди на 10ГГц d = 0,6 мкм, это позволяет использовать тонкие (10-20 мкм) слои хороших проводников для уменьшения потерь.

Частотная дисперсия характерна также для плазмы (ионизированный газ), для нее:

;

;

.

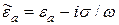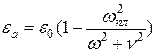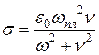Где n– частота столкновений электронов с нейтральными молекулами,

w_пл – собственная (плазменная) частота, при которой при n = 0, e_а = 0.

,

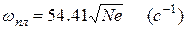где Ne – электронная концентрация.

Если потери отсутствуют, то фазовая скорость выражается:

.

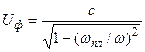Скорость переноса информации (скорость перемещения в пространстве энергии, или медленной огибающей, или группы волн):

,

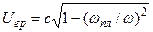Эта формула справедлива для узкополосных сигналов (можно применять для радиоимпульсов и т.д.). Такая частотная зависимость приводит к расплыванию (увеличению длительности) импульсов.

Рассмотрим поляризацию волн. Полагаем, что вектор Е имеет две составляющие, 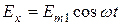и 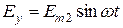. Найдем положение кривой, которая служит геометрическим местом концов вектора Е суммарного процесса. Перепишем составляющие в виде: 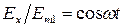, . Возводим их в квадрат и складываем:

.

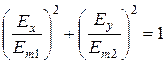Это уравнение эллипса, а про волну говорят, что это эллиптически поляризованная волна (см. рисунок 2.1).

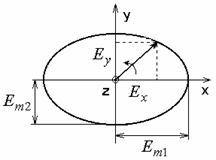
Рисунок 2.1 – Эллиптически поляризованная волна

В этом случае вектор Е вращается против часовой стрелки, если смотреть с конца i_z – лево поляризованная волна.

Частные случаи:

– Равна нулю одна из составляющих или сдвиг фаз между ними равен нулю. Тогда конец вектора Е перемещается вдоль линии произвольно, в общем случае, ориентированной относительно системы координат. Волна – линейно поляризованная.

– Равны амплитуды Е_m1 = Е_m2, а сдвиг фаз - 90°. Тогда кривая окружность, волну называют волной с круговой поляризацией.

Легко заметить, что суперпозиция двух волн с линейными поляризациями, сдвинутых по фазе и пространственно на 90°, дают эллиптически поляризованную волну, две волны с круговыми поляризациями и противоположными направлениями вращения, в результате суперпозиции дают волну линейно поляризованную.

Лекция №3. Падение плоских электромагнитных волн на границу раздела двух сред

Граничные условия – соотношения, показывающие связь между значениями векторов ЭМП в разных средах, у поверхности раздела называют граничными условиями.

Полная система граничных условий состоит из четырех формул:

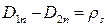; (3.1)

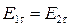; (3.2)

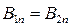; (3.3)

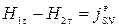. (3.4)

Формула (3.1) показывает, что нормальная компонента вектора D претерпевает скачек на величинуповерхностного заряда 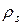. На самом деле поверхностных зарядов не бывает, толщина слоя конечна и D меняется постепенно. Но математическая модель 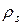удобнее.

Если свободные заряды на границе раздела сред отсутствуют 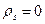, то для вектора Е:

.

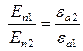Нормальная компонента вектора Е претерпевает разрыв.

Формула (3.2) показывает, что тангенсальная составляющая вектора Е, непрерывна при переходе через границу раздела двух сред.

Для вектора B нормальные составляющие непрерывны (3.3), а тангенсальные составляющие вектора Н претерпевает скачек на величину плотность поверхностного тока 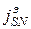(3.4), направленного ортогонально вектору 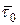(или его составляющей).

На поверхности раздела с идеальным проводником 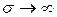, внутри которого поле отсутствует, согласно уравнению Максвелла будут справедливы следующие граничные условия:

;

;

;

.

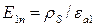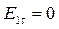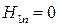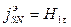Рассмотрим падение плоских электромагнитных волн на границу раздела двух сред. Границу раздела будем полагать бесконечно протяженной. Плоскость, проходящая через нормаль к границе раздела параллельно направлению распространения, называют плоскостью падения.

Если вектор Е перпендикулярен этой плоскости, то волна – нормально поляризованная, если параллелен, волна – параллельно поляризованная.

Любую другую ориентацию вектора Е следует рассматривать как суперпозицию .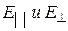

Падение волны с нормальной поляризацией на границу раздела двух сред изображено на рисунке 3.1.

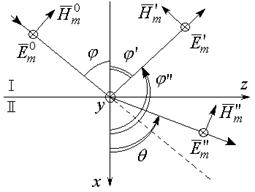
Рисунок 3.1 – Падение волны с нормальной поляризацией на границу раздела двух сред

Амплитуды напряженностей электрического и магнитного поля падающей, отраженной и преломленной волны определяются выражениями:

;

;

;

;

;

.

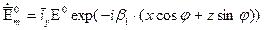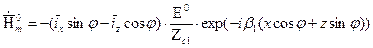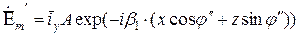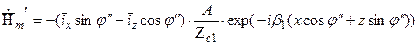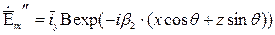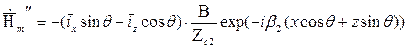Падающая волна под углом j частично (или полностью) отражается от границы раздела сред под углом j” и частично (или полностью) проходит во вторую среду под углом θ. Амплитуды напряженности электрического поля отраженной и преломленной волны обозначены в этих выражениях как некоторые величины А и В соответственно. Можно считать, что ориентация векторов 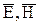относительно направления распространения не меняется.

Волновое сопротивление первой среды:

.

Волновое сопротивление второй среды:

.

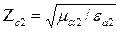Из граничных условий следует равенство тангенсальных составляющих: 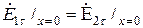. Граничные условия должны выполняться при любых z. Это возможно только, если зависимость от z для всех трех векторов напряженности электрического поля одинаковы. Отсюда вытекают два закона:

– угол падения равен углу отражения

;

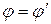– и закон Снелля

,

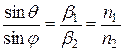где n - показатель преломления среды

.

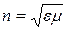Из закона сохранения энергии определим постоянные А и В на границе раздела (А и В амплитуды отражённой и преломлённой волн соответственно):

А = RЕ°;

В = ТЕ°,

где R - коэффициент отражения, T - коэффициент преломления (коэффициенты Френеля).

В случае нормальной поляризации:

1+R_^=T_^;

1-R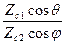_^=Т_^.

Модуль R характеризует соотношение между амплитудами падающей и отражённой волны, а аргумент - сдвиг фаз между этими полями:

R_^ =;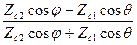

T_^ =.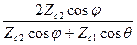

Вывод при параллельной поляризации аналогичен, получаем:

R_{| |}=;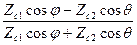

T_|| =.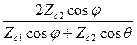

При нормальном падении ЭМВ, когда j = 0, плоскость падения становится неопределённой и различие поляризаций пропадает:

R_^= - R_||=;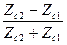

T_^= T_|| =.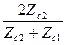

Знак ’’минус’’ за счёт того, чтоR_^ и T_^ коэффициенты по электрическому полю, R_êê и T_êê – по магнитному.

Для обычных диэлектриков существует угол падения, при котором падающая волна целиком проходит во вторую среду называемый – Угол Брюстера. Это возможно в следующих случаях:

– необходимо, чтобы R_^ и R_êê равнялись 0 для любого угла падения j, что для реального диэлектрика означает 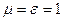, т.е. электромагнитные свойства вещества неотличимы от свойств вакуума, если он – первая среда, или (m/e = 1): Z_С2 = Z_С1;

– для параллельной поляризации, когда :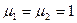

;

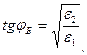– для нормальной поляризации, когда :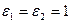

.

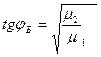От границы раздела обычных диэлектриков волна с нормальной поляризацией отражается всегда.

Волна с эллиптической поляризацией отражается от границы всегда.

Отметим условия, при которых вещество полностью отражает падающие на него электромагнитные волны:

– если 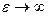при конечном значении m, то коэффициенты отражения стремятся к предельным значениям: R_êê = - 1; R_^ = 1. К этому предельному случаю очень близко подходят металлы, у них e имеет большую мнимую часть. Металлы – почти идеальные зеркала для электромагнитных волн.

– вещества, у которых при конечной значение e, величина магнитной проницаемости m была бы весьма велика, то для них: R_êê=1; R_^= -1. Например,÷Rç стремится к 1 для критической плазмы (e £ 0);

– в случае, когда волна распространяется из оптически плотной среды в менее плотную оптическую среду (n₂<n₁):

.

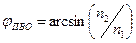Коэффициент отражения от системы из n слоёв описывается следующим выражением:

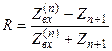
где

.

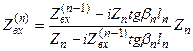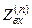- входной импеданс системы, причём, если угол падения не равен нулю, то следует использовать:

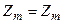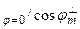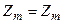ç;

ç.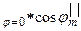

при перпендикулярной и параллельной поляризациях соответственно. Углы j рассчитывают исходя из законов Снелля.

Частные случаи:

– Полуволновой слой, когда

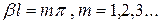
Входной импеданс: .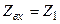

Коэффициент отражения:

,

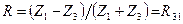то есть полуволновой слой не оказывает никакого действия на падающую волну. В частности, если Z₁ = Z₃, то отражение отсутствует (можно использовать как фильтр частот и направлений).

– Четвертьволновой просветляющий слой, когда

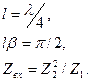
Коэффициент отражения будет равен нулю, если сопротивление: 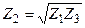, среднегеометрическое. Используют при согласовании.

С учётом всего вышесказанного изобразим зависимость R и T от j на границе раздела (качественно) (см. рисунок 3.2).

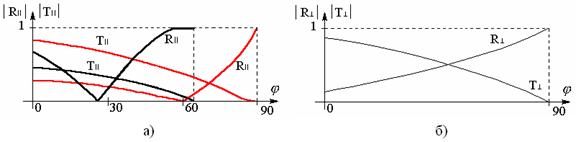
Рисунок 3.2 – Зависимости коэффициента отражения и коэффициента преломления от угла падения: а) для параллельной поляризации;

б) для нормальной поляризации

Зависимость от толщины слоя носит осциллирующий характер, причём если в слое есть потери, то амплитуда осцилляций стремится к постоянной величине – дальняя граница перестаёт оказывать влияние (волны затухают, не доходя до неё).

Лекция №4. Падение плоской электромагнитной волны на границу раздела с немагнитной хорошо проводящей средой. Линии передачи

Рассмотрим падение плоской электромагнитной волны из воздуха под углом j на границу раздела с немагнитной хорошо проводящей средой. Такая материальная среда имеет комплексный показатель преломления

Дата добавления: 2014-01-05