Свойства алгебраических операций

Упражнения

1. Сформулируйте условия, при которых операция, заданная на множестве X:

а) будет алгебраической; б) не будет алгебраической.

2. Объясните, почему сложение и умножение являются алгебраиче­скими операциями на множестве 2 целых чисел, а деление не является.

3. На множестве X= {-1,0,1} заданы сложение, умножение и вычитание. Являются ли они алгебраическими на этом множестве?

4. Являются ли алгебраическими операции: сложение, умножение,
деление и вычитание, заданные на множестве X, если:

a) Х - множество четных натуральных чисел;

б) X - множество нечетных натуральных чисел;

в) Х- множество натуральных чисел, кратных 5?

5. Среди следующих высказываний укажите истинные, ответ обос­нуйте:

а) Множество N натуральных чисел замкнуто относительно умножения.

б) Множество Q рациональных чисел замкнуто относительно де­ления (деление на нуль не рассматривается).

в) Множество Z целых чисел замкнуто относительно вычитания и деления.

г) Множество Z целых чисел замкнуто относительно вычитания или деления.

6. Являются ли алгебраическими на множестве натуральных чисел следующие операции:

а) возведение в степень;

б) нахождение наибольшего общего делителя двух чисел;

в) нахождение наименьшего общего кратного двух чисел?

7. Дано множество {а, Ь, с}. Составьте множество X всех его подмножеств. На этом множестве X рассмотрите операции пересечения и объединения. Являются ли они алгебраическими?

8. В начальном курсе математики сложение рассматривают сначала на отрезке натуральных чисел от 1 до 9 (включительно), затем на отрезке от 1 до 100, затем от 1 до 1000, Является ли оно алгебраиче­ской операцией на этих множествах?

Известно, что сложение и умножение чисел обладает свойствами коммутативности, ассоциативности, умножение дистрибутивно отно­сительно сложения. Аналогичными свойствами обладают объедине­ние и пересечение множеств.

Рассмотрим свойства алгебраических операций, определив их в общем виде. При этом условимся алгебраические операции обозна­чать символами: * (читается - «звездочка») и ^о (читается - «кружок»).

Важнейшим свойством алгебраических операций является свойство ассоциативности.

Определение. Алгебраическая операция *, заданная на множестве X, называется ассоциативной, если для любых элементов х, у и z из множества X выполняется равенство

(x*y)*z=x*(y*z).

Если операция * обладает свойством ассоциативности, то можно опускать скобки и писать x*у*z вместо (х*у)*z и х*(у*z).

Например, ассоциативно сложение натуральных чисел: для любых на­туральных чисел х, у и z выполняется равенство (х + у) + z = x + (у + z). Ассоциативно сложение рациональных и действительных чисел. По­этому сумму нескольких чисел можно записывать без скобок.

Существуют алгебраические операции, не обладающие свойством ассоциативности. Так, не является ассоциативным вычитание целых чисел: существуют целые числа х, у и z, для которых (х - у) - z ≠ х - (у - z). Например, (12 - 7) - 3 ≠ 12 - (7 - 3).

Ассоциативность алгебраической операции * позволяет записывать без скобок все выражения, содержащие лишь эту операцию, но пере­ставлять входящие в это выражение элементы, вообще говоря, нельзя. Перестановка элементов возможна лишь в случае, когда операция * коммутативна.

Определение. Алгебраическая операция * на множестве X называ­ется коммутативной, если для любых двух элементов х и у из мно­жества X выполняется равенство

х*у = у*х.

Примерами коммутативных операций могут служить сложение и умножение натуральных чисел, поскольку для любых натуральных чисел х и у выполняются равенства х + у = у + х, х · у = у · х. Эти равен­ства справедливы не только для натуральных чисел, но и для любых действительных чисел, следовательно, на множестве действительных чисел сложение и умножение тоже коммутативны.

Существуют алгебраические операции, не обладающие свойством коммутативности. Так, не является коммутативным вычитание целых чисел: существуют целые числа х и у, для которых х - у ≠ у - х. На­пример, 12-7≠7-12.

Если на множестве X заданы две алгебраические операции * и ^о, то они могут быть связаны друг с другом свойством дистрибутивности.

Определение. Алгебраическая операция ^о называется дистрибу­тивной относительно алгебраической операции *, если для любых элементов х, у и z из множества X выполняются равенства:

1) (х*y)^оz = (x ^o z)*(y ^o z) и 2) z ^o (х*у) = (z ^o х)*(z ^о у).

Если выполняется только равенство 1), то операцию ^о называют дистрибутивной справа относительно операции *; если же выполняет­ся только равенство 2), то операцию ^о называют дистрибутивной слева относительно операции *.

Выясним, в каких случаях различают дистрибутивность справа и слева.

Рассмотрим на множестве натуральных чисел две операции: воз­ведение в степень (она соответствует операции ^о в равенствах 1 и 2) и умножение (она соответствует операции * в равенствах 1 и 2). Тогда, согласно равенству 1, имеем: (х·у)^z - = х^z-у^z. Как известно из алгебры, полученное равенство справедливо для любых натураль­ных чисел х, у и z, т.е. возведение в степень дистрибутивно справа относительно умножения. В соответствии с равенством 2, получа­ем х ^уz = х^у-х^z. Но это равенство выполняется не всегда, т.е. опера­ция возведения в степень не является дистрибутивной слева отно­сительно умножения. Такая ситуация является следствием того, что возведение в степень - операция, не обладающая свойством коммутативности.

Если взять сложение и умножение натуральных чисел, то, как из­вестно, умножение дистрибутивно относительно сложения: для лю­бых натуральных чисел х, у и z выполняются равенства

(x+y)·z + x·z + y·z и z·(x+y) = z·x + z·y

А так как умножение коммутативно, то не имеет значения, где писать множитель z - справа от суммы х + у или слева от нее. Поэтому в школьном курсе математики не различают дистрибутивность слева и справа, а говорят просто о дистрибутивности умножения относительно сложения.

Выясним роль свойства дистрибутивности в преобразованиях вы­ражений. Если операция ^о дистрибутивна относительно операции * и обе операции ассоциативны, то в любом выражении, содержащем лишь эти две операции, можно раскрыть все скобки, перед которыми (или за которыми) стоит знак °. Проиллюстрируем сказанное на при­мере преобразования выражения (x + у)·(z + р). Так как умножение дистрибутивно относительно сложения, то

(x + у)·(z + р)= x·(z + р) + у·(z + р)= (x·z + x·р) + (у·z + y·р).

А поскольку сложение ассоциативно, то последнюю запись можно за­писать без скобок. Следовательно, (x + у)·(z + р)=)=x·z + x·р +у·z + y·р.

Часто в множестве, на котором рассматривается алгебраическая операция, выделяются особые элементы, называемые в алгебре ней­тральными и поглощающими.

Определение. Элемент е из множества X называется нейтраль­ным относительно алгебраической операции *, если для любого эле­мента х из множества X выполняются равенства х*е=е*х =х.

Доказано, что если нейтральный элемент относительно алгебраической операции существует, то он единственный.

Определение. Элемент р из множества X называется поглощаю­щим относительно алгебраической операции *, если для любого эле­мента х из множества X выполняются равенства х*р=р*х=р.

Если поглощающий элемент относительно алгебраической опера­ции существует, то он единственный.

Так, в множестве Z_о целых неотрицательных чисел нуль является нейтральным элементом относительно сложения, поскольку для любого х из множества Z_о выполняются равенства х + 0 = 0 + х = х. Это же число нуль является поглощающим элементом относительно умноже­ния: для любого x из множества Z_о верны равенства: х· 0 = 0·х = 0.

Как известно, вычитание чисел является операцией, обратной сло­жению. Но чтобы дать определение обратной операции в общем виде, надоопределить понятие сократимой операции.

Определение. Алгебраическая операция *, заданная на множестве X, называется сократимой, если из условий а*х =а*у и х*а =у*а следует, что х =у.

Например, сократимо сложение натуральных чисел: из равенств а+х=а+у и х+а=у+а следует, что х= у.

Определение. Пусть * - сократимая и коммутативная алгебраи­ческая операция, заданная на множестве X. Тогда операция ^о назы­вается обратной для операции *, если х ^о у = z тогда и только тогда, когда у * z = х.

Тот факт, что вычитание на множестве целых чисел есть операция, обратная сложению, означает: z = х - у тогда и только тогда, когда у + z = х.

Множество X с заданными на нем алгебраическими операциями принято называть алгеброй. В начальном курсе математики в основном изучают множество Z_о целых неотрицательных чисел, которое являет­ся объединением множества натуральных чисел и нуля: Z_о = N U{0}. На этом множестве рассматриваются алгебраические операции сло­жения и умножения. Используя язык современной математики, можно сказать, что в начальной школе изучают алгебру (Z_о, +, •). Ее основ­ные характеристики:

1) Сложение и умножение на множестве Z_о ассоциативно и комму­тативно, а умножение дистрибутивно относительно сложения, т. е.:

(V х,у € Z_о) х + у = у + х;

(V х,у € Z_о) х·у = у·х;

(V х,у,z € Z_о) (х + у) + z = х + (у + z);

(V х,у,z € Z_о) (х·у)·z = х·(у·z);

(V х,у,z € Z_о) (х +у)·z = х·z +у· z.

2) Сложение и умножение сократимы (исключая сокращение произ­ведения на нуль), т.е. для любых целых неотрицательных чисел х,у и а справедливы утверждения:

х + а= у + а => х = у

х·а = у·а => х = у.

3) Нуль является нейтральным элементом относительно сложения и поглощающим относительно умножения:

(V х € Z_о) х + 0 = 0 + х = x:;

(V х € Z_о) х· 0 = 0· x = 0.

Единица является нейтральным элементом относительно умножения:

(V х,у € Z_о) х •1 = 1• x = x.

4) Сократимость сложения и умножения целых неотрицательных чисел позволяет определить в Z_о частичные алгебраические операции вычитания и деления как обратные соответственно сложению и умно­жению (исключая деление на нуль):

x-у = z ó у + z = x

х:у~2 ó у-z = х.

5) Вычитание и деление обладают свойствами:

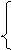(a-c)+b, если а≥с

(а+b) – c= a+(b-c), если b≥c

а - (b + с) = (а - b) - с = (a - с) - b, если a ≥ b + с;

(a+b):c = a:c+b:c, если a:c и b:c;

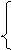(a:c)·b, если а:с

(а·b): c= a·(b:c), если b:c

а:(b-с) = (а:b):с= (а:с):b, если a:b и a:c

Названные характеристики алгебры (Z_о, +, •) присутствует (явно или неявно) в любом начальном курсе математики.

Дата добавления: 2014-01-06