Решение линейных рекуррентных уравнений

Пример. Найдем производящую функцию к числам Фибоначчи: F₀=F₁=1, F_n+2=F_n+F_n+1, n³0.

Производящая функция F(t) для последовательности F(0),F(1),F(2),… удовлетворяет уравнению

F(t)==1+t+=

1+t+t²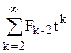+t=

1+t+t²F(t)+t(F(t)-1)= 1+(t+t²)F(t),

т. е. F(t)=(1-t-t²)^-1.

Найдя корни уравнения 1-t-t²=0, получаем разложение

1-t-t²=(1-аt)(1-bt), где а=(1+Ö5)/2, b==(1-Ö5)/2.

Используя метод неопределенных коэффициентов, найдем

=+

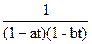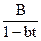
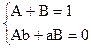
т. е.

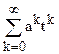F(t)=A(1-at)^-1+B(1-bt)^-1=A+B=t^k

и

F_k=+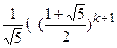

Замечание. этот метод можно перенести на произвольное линейное уравнение с постоянными коэффициентами.

Задача 1. Пусть задана последовательность Фибоначчи

F₀=F₁=1, F_n+2=F_n+F_n+1, n³0.

Рассмотрим множество последовательностей из нулей и единиц длины n, в которых нет двух рядом стоящих единиц. Пусть таких последовательностей A(n). Тогда А(n)=F_k+1.

Доказательство.

Имеем А(0)=1, так как существует только одна – пустая, такая последовательность; А(1)=2, так как существует две такие последовательности – ‘0’ и ‘1’.

Заметим, что число последовательностей длины n, у которых на n месте находится нуль, равно А(n-1).

Все последовательности длины n+1 могут быть построены из последовательностей длины n приписыванием к каждой из них на n+1 место нуля и, кроме того, тем из них, которые на n месте имеют ноль, можно также приписать единицу. Таким образом, А(n+1)=A(n)+A(n-1)=F_n+1+F_n=F_n+2.

Задача 2. "n>0 А(n)==.

Доказательство.

А(n) можно получить следующим образом:

Заметим, что каждая такая последовательность длины n может содержать не более [(n+1)/2] единиц. Подсчитаем, сколько существует последовательностей, содержащих k единиц, 0£k£[(n+1)/2]. Если последовательность имеет к единиц, то она содержит n-k нулей. Рассмотрим последовательность из n-k нулей. Тогда в этой последовательности имеется n-k+1 мест для расстановки k единиц. Т. е. общее число требуемых последовательно

стей длины n,содержащих k единиц, равно . Таким образом,

A(n)= .

Производные сложных функций (Формула Бруно)

Сложная функция – это функция от функции. Ей можно придать стандартную форму экспоненциальной (или обычной) производящей функции, воспользовавшись ее производными. Выражая производную сложной функции через ее компоненты, приходим к некоторой совокупности полиномов – полиномов Белла, – характерных для многих комбинаторных и статистических задач.

Положим

А(t)=f[g(t)] (1)

и

A(t)=A_n, [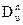f(u)]_u=g(t)=f_n, g(t)=g_n, где D_t=d/dt, D_u=d/du

Затем последовательным дифференцированием (1) получим

А₁=f₁g₁

А₂=f₁g₂+f₂

А₃=f₁g₃+ 3f₂g₂g₁+f₂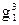

В общем виде можно записать

А_n=f₁A_n1+ f₂A_n2+…+f_nA_nn=

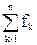=A_n,k(g₁, g₂,… g_n) (2)

Отметим, что коэффициенты A_n,k зависят только от производных g₁, g₂,… g_n и не зависят от f_k. Следовательно, они могут быть определены специальным выбором f; удобно положить f(u)=exp(au), где а – постоянная. Тогда

f_k=а^k exp(ag), g=g(t)

и

e^-age^ag=ΣA_n,k(g₁, g₂,… g_n)a^k=

A_n(a, g₁, g₂,… g_n), (3)

где вторая строка – сокращенная запись первой

В этих обозначениях (2) принимает вид

А_n=A_n(a, g₁, g₂,… g_n), f^k≡f_k, (2a)

где

А₀=f₀=A(t)

Соотношение (3) полностью определяет полиномы A_n(a,g₁,g₂,…g_n) и с помощью (2а), – производные A_n. Можно заметить, что в обозначениях Белла

A_n(1, y₁, y₂,… y_n)=Y_n(y₁, y₂,… y_n)=e^-ye^y,

y≡y(x).

С целью получения явного выражения для полиномов Белла обозначим кратко

A_n(a, g₁, g₂,… g_n)

через А_n(a) и используем формулу Лейбница для дифференцирования произведения

А_n+1(a)=e^-agDⁿ(De^ag)=

=a^-agaDⁿ(g₁ e^ag)=

=а(e^-agD^n-ke^ag)D^kg₁=

=аA_n-k(a)g_k+1=

=ag(A(a)+g)ⁿ; (A(a))^k≡A_k(a), g^k≡g_k (4)

Частными случаями соотношения (4) при А₀(a)=1 являются соотношения

А₁(a)=ag₁

А₂(a)=ag₂+ag₁А₁(a)=ag₂+a²

А₃(a)=ag₃+ 2ag₂А₁(a)+ag₁А₂(a)= ag₃+ 3a²g₂g₁+a³,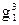

что согласуется с результатами, предшествующими (2)

Далее, соотношение (4) влечет за собой соотношение для экспоненциальной производящей функции

exp(uA(a))=(a)uⁿ/n!=

=exp(a[ug₁+u²g₂/2!+…])=

=exp(aG(U), (5)

в котором

G(u)=exp(ug) – g₀, gⁿ≡g_n

Дифференцированием (5) и приравниванием коэффициентов при uⁿ получаем (4).

Наконец, раскрывая (5) с помощью полиномиальной теоремы и приравнивая коэффициенты при uⁿ получаем искомую формулу

А_n(a)=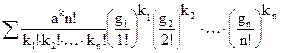, (6)

в которой k₁ +k₂+…+k_n=k и сумма берется по всем решением в неотрицательных целых числах уравнения k₁ +2k₂+…+nk_n=n, или по всем разбиениям n. Отсюда, имея в виду (2а), получаем соотношение, известное как формула Бруно

А_n=А_n(f)= (5а)

Замечание. Если A(t) разлагается в ряд Тейлора, т. е. если

A(t+u)=exp(uA(t)), Aⁿ(f)≡A_n(f),

то

=A_n(f) при t=0,

A(t)= exp(uA⁰), (A⁰)ⁿ≡.

Дата добавления: 2014-01-06