Связные графы

Пусть G – граф и v₀, v₁, v₂,…, v_n – последовательность вершин графа G, такая, что вершина v_i смежна с вершиной v_i+1 при i = 0, 1, …,n-1. Такая последовательность вместе с n ребрами { v_i, v_i+1}, 0≤i≤n-1, называется маршрутом длины n. Если ребра в маршруте различные, то он называется цепью. Если в маршруте различны все вершины (а следовательно, и ребра), то называется простой цепью. Связным графом называется граф, в котором любые две различные вершины простой цепью.

Число помеченных связных графов порядка 4 может быть вычислено тривиальным образом и равно 38.(Проверьте!).

Подграф H графа G имеет V(H)ÍV(G) и X(H)ÍX(G). Компонента графа представляет собой максимальный связный подграф. Граф с корнем (и корневой граф) имеет одну выделенную вершину, называемую корнем. Два корневых графа называют изоморфными, если существует взаимно однозначная функция, отображающая множество вершин одного графа на множество вершин другого графа, которая сохраняет не только смежность вершин, но и корни [6]. Аналогичное требование накладывается и при описании корневых помеченных графов. Это понятие можно сейчас использовать для получения следующей рекурсивной формулы. Пусть С_p – число связанных помеченных графов порядка р.

Теорема. Число С_p связанных помеченных графов удовлетворяет соотношению

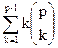
С_p= -C_k. (5)

Доказательство.

Заметим, что если в помеченном графе делать корнями разные вершины, то получатся разные корневые помеченные графы. Следовательно, число корневых помеченных графов, в которых порядка p равно pG_p. число корневых помеченных графов, в которых корень находится в компоненте, содержащей в точности k вершит равно kC_k .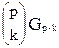

Суммируя эти произведения по k от 1 до p, мы опять получаем выражение для корневых помеченных графов, а именно

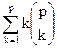С_kG_p-k.

Для дальнейших построений нам потребуется важное свойство экспоненциальных производящих функций для графов:

Для всякого к =1,2,3…обозначим через а_k число способов, которым можно пометить все графы порядка k, обладающие некоторым свойством P(a), пусть a(t)= 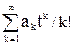экспоненциальная производящая последовательности а_k. Предположим также, что b(t)=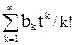другая экспоненциальная производящая функция для класса графов, удовлетворяющих свойству P(b).

Следующая лемма дает полезную интерпретацию коэффициентов произведения а(t)∙b(t) этих двух производящих функций.

Лемма пересчета помеченных графов. Коэффициент при t^k/k! в а(t)∙b(t) равен числу упорядоченных пар (G₁,G₂) двух непересекающихся графов, где G₁ обладает свойством P(a), где G₂ обладает свойством P(b), k – Число вершин в G₁ÈG₂ и пометки от 1 до k распределены на графе G₁ÈG₂.

Для иллюстрации этой леммы положим, что С(t) – экспоненциальная производящая функция для помеченных связных графов: C(t)=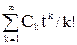

Тогда С(t)∙С(t) является производящей функцией для упорядоченных пар связных графов. Разделив этот ряд на 2, получаем производящую функцию для помеченных графов, имеющих в точности две компоненты. Аналогично, Сⁿ(t)/n! имеет при t^k/k коэффициент, равный числу помеченных графов порядка k, содержащих в точности n компонент. Если через G(t) обозначим экспоненциальную производящую функцию для помеченных графов, то

G(t)= . (6)

Таким образом, мы имеем следующее экспоненциальное соотношение между

G(t) и С(t), найденное Риделлом (1951).

Теорема. Экспоненциальные производящие функции G(t) и С(t) для помеченных графов и для помеченных связных графов удовлетворяют соотношению

1+ G(t)=e^С(t). (7)

Замечание. 1. Это равенство остается справедливым и для мультиграфов.

Риордан получил следующее рекуррентное соотношение для С_р:

С_p=(2^k-1)C_kC_p-k. (8)

Кроме того, очевидно, что если известна экспоненциальная производящая функция для некоторого класса графов, то экспоненциальная производящая функция для соответствующих связных графов получается формальным логарифмированием первого ряда, точно так же как в теореме для всех графов.

Поэтому мы можем сформулировать следующий общий результат.

Следствие. Если 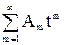/m!=exp(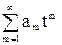/m!), то для m≥1

a_m=A_m -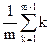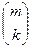a_kA_m-k. (9)

Задачи 1. Построить производящую функцию для связных помеченных орграфах;

2.найти перечислительную формулу для помеченных (p,q)-графов, не имеющих изолированных вершин.

Дата добавления: 2014-01-06