Функция

Отображение

Полностью определенное соответствие называется отображением.

Пусть A и B – произвольные непустые множества. Если задано такое соответствие, при котором область определения совпадает с областью отправления (A_R º A), то есть каждому элементу a Î A может быть сопоставлен хотя бы один элемент b Î B, то говорят, что задано отображение G множества A на множество B. Для обозначения отображения используется запись

G: A → B.

С математической точки зрения отображение определяется тройкой множеств < A, B, G > и является частным случаем соответствия. Графически отображение соответствует рис. 4.2.

Если каждому элементу a Î A отображение G ставит в соответствие некоторое подмножество G (a)Ì B, то образом элемента a будет подмножество G (a), а отображение G будет называться многозначным отображением. Если же | G (a)|=1, то имеем дело с однозначным отображением.

Отображения бывают инъективными, сюръективными, функциональными и биективными. Студентам предлагается самим придумать примеры отображений данных типов.

Функцией f называется функциональное соответствие, то есть такое, при котором для <a₁, b₁>Îf и <a₂, b₂>Îf из a₁=a₂ следует b₁=b₂. Обозначение функции:

f: A®B или f (a) = b.

Здесь элемент a называют аргументом функции, элемент b – значением функции.

Если область определения функции совпадает с областью отправления, то функцию называют полностью определенной. В противном случае она считается частично определенной или частичной функцией.

Если | B |=1, то функция называется функцией-константой.

Функция называется инъективной, если

" a ₁, a ₂, b: b = f (a ₁), b = f (a ₂) Þ a ₁= a ₂,

то есть каждому значению функции соответствует единственное значение аргумента.

Функция называется сюръективной, если

" b Î B $ a Î A: b = f (a),

то есть каждому значению b соответствует некоторый аргумент a.

Функция называется биективной, если она одновременно сюръективна и инъективна.

Студентам предлагается самостоятельно нарисовать графические представления различных типов функций по аналогии с рисунками 4.2-4.6.

В качестве примера рассмотрим три функции, заданные на множестве действительных чисел и принимающих значения в этом же множестве:

1. Функция f(x)=e^x. Она инъективна (поскольку каждое значение функции определено только для одного аргумента), но не сюръективна, (поскольку отрицательным значениям функции не сопоставлено ни одно значение аргумента).

2. Функция f(x)=x³-x. Она сюръективна (так как может принимать все значения на множестве действительных чисел), но не инъективна (например, значение, равное нулю, она принимает на трех различных аргументах: при x=0, x=1 и x=-1);

3. Функция f(x)=2x+1 – биективна (в качестве аргументов и значений могут выступать все элементы множества действительных чисел, причем каждому значению аргумента соответствует только одно значение функции, и наоборот).

Функция типа A ₁´ A ₁´…´ A _n® B называется n-местной функцией. В этом случае принято считать, что функция имеет n аргументов:
f (a ₁, a ₂, …, a _n) = b, где a ₁Î A ₁, a ₂Î A ₂, …, a _nÎ A _n, b Î B. Например, сложение, умножение, вычитание и деление являются двухместными функциями на множестве вещественных чисел R, то есть функциями типа R ²® R.

Если соответствие, обратное к функции f: A ® B является функциональным, то оно называется функцией, обратной к f и обозначается
f ^–1. Очевидно, что в обратном соответствии образы и прообразы меняются местами, поэтому для существования обратной функции f ^–1 требуется, чтобы каждый элемент из области значения 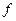имел бы единственный прообраз. Это означает, что для функции f: A ® B обратная функция f ^–1 существует тогда и только тогда, когда f является биективным соответствием между своей областью определения и областью значений.

Например, функция sin(x) имеет тип R ® R. Отрезок [–p/2; p/2] она взаимно однозначно отображает на отрезок [–1; 1]. Поэтому для неё на отрезке [–1; 1] существует обратная функция arcsin(x).

Лекция 5

Дата добавления: 2014-01-06