Алгебра высказываний

Основным понятием математической логики является понятие «простого высказывания». Под высказыванием обычно понимают всякое повествовательное предложение, утверждающее что-либо о чем-либо, и при этом мы можем сказать, истинно оно или ложно в данных условиях места и времени (но не то и другое вместе).

Приведем пример высказываний:

1. Через Донецк протекает река Кальмиус.

2. Киев – столица Украины.

3. Окунь не рыба.

4. Число 6 делится на 3.

5. Студент – тоже человек.

6. Я лгу.

7. Да здравствуют наши спортсмены!

Здесь примеры 1-5 являются высказываниями (1,4, 5 – истинны, 2 и 3 – ложны). Примеры 6 и 7 не являются высказываниями, поскольку о них нельзя однозначно сказать, истинны они или ложны.

В алгебре высказываний не рассматривают внутреннюю смысловую сущность высказываний, а ограничиваются рассмотрением их свойства представлять истину или ложь. При этом сами высказывания обычно обозначают латинскими буквами, например A, B, C, а их значения, то есть истину или ложь, соответственно цифрами 1 и 0. Так, если высказывания 1-5 обозначить латинскими буквами от A до E, то можно записать, что A=1, B=0, C=0, D=1, E=1.

Высказывание является простым, если оно не может быть разложено на несколько более простых высказываний, и сложным – в противном случае. В обычной речи сложные предложения образуются из простых с помощью связок: «и», «или», «не», «если...то» и других. Например:

1. Светит солнце и идет снег.

2. Студент сдает все экзамены или студент отчисляется из университета.

3. Не каждый день платится стипендия.

4. Если преподаватель опаздывает на 15 минут, то студенты могут идти домой.

Подобные словесные связки принято рассматривать как операции над высказываниями. Операции над высказываниями позволяют определить истинность или ложность сложного высказывания на основе истинности или ложности его составляющих. Совокупность операций над высказываниями образует алгебру высказываний или алгебру логики. Алгебру логики называют алгеброй Буля или булевой алгеброй, по имени английского математика Джорджа Буля, разработавшего в XIX веке её основные положения.

Пусть даны два произвольных высказывания a и b.

1. Выражение A & B (читается: «A и B») означает высказывание, истинное только в том случае, когда оба высказывания A и B истинны. Такое высказывание является конъюнкцией высказываний A и B. Операция конъюнкции обычно обозначается символом «&», реже – символами «Ù», «*», «×». Эта операция соответствует союзу «и» в обычной речи и иногда для краткости называется операцией «И». Однако в повседневной речи не принято соединять союзом «и» два высказывания, далекие по содержанию. В алгебре логики операция конъюнкции может быть применена к любым двум высказываниям. Например, для высказываний «два меньше пяти» и «трава зеленая» их конъюнкция «два меньше пяти и трава зеленая» является истинным высказыванием, поскольку оба высказывания, образующих конъюнкцию, истинны.

2. Выражение A Ú B (читается: «A или B») означает высказывание, истинное в том случае, если хотя бы одно из высказываний A или B является истинным. Такое высказывание называется дизъюнкцией высказываний A и B. Символ «Ú» обозначает операцию дизъюнкции; иногда вместо символа «Ú» используют символ «+». Операция дизъюнкции иногда для краткости называется операцией «ИЛИ».

В обычной речи дизъюнкция соответствует союзу «или», применяемому в неисключающем смысле. Дело в том, что в повседневной речи союз «или» может иметь два смысловых значения: неисключающее и исключающее. В первом случае подразумевается, что из двух высказываний, по крайней мере, одно истинно, а может быть, и оба истинны. Например: «В жаркую погоду пьют воду или едят мороженое». Во втором случае предполагают, что из двух высказываний истинным является только одно: «Сегодня мы поедем на экскурсию или пойдем на пляж». Дизъюнкция высказываний соответствует первому случаю.

3. Выражение 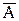(читается: «не A») означает высказывание, которое истинно, когда A – ложно, и наоборот. Такое отрицание называется отрицанием или инверсией высказывания. Отрицание обозначается черточкой на буквой или, реже, символом ¬, поставленным сразу перед буквой: «¬A». В обычной речи этой операции соответствует частица «не». Например, для истинного высказывания «восемь делится на четыре» отрицанием является ложное высказывание «неверно, что восемь делится на четыре» или «восемь не делится на четыре». Для ложного высказывания «февраль – летний месяц» отрицанием является истинное высказывание «неверно, что февраль – летний месяц» или «февраль – не летний месяц».

4. Выражение A ~ B (читается: «A эквивалентно B», «для того, чтобы A, необходимо и достаточно, чтобы B», «A тогда и только тогда, когда B», «A равносильно B») означает высказывание, которое истинно тогда и только тогда, когда A и B оба истинны или оба ложны. Такое высказывание называется эквивалентностью высказываний A и B. Символ ~ означает операцию эквивалентности. В обычной речи этой операции соответствует связка «тогда и только тогда».

Рассмотрим пример. Пусть даны два высказывания: A=«Компьютер может производить вычисления» и B=«Компьютер включен». Составное высказывание, полученное с помощью операции эквивалентности, истинно, когда оба высказывания либо истинны, либо ложны:

«Компьютер может проводить вычисления тогда и только тогда, когда компьютер включен».

«Компьютер не может производить вычисления тогда и только тогда, когда компьютер не включен».

Составное высказывание, полученное с помощью операции эквивалентности, ложно, когда одно высказывание истинно, а другое ложно:

«Компьютер может производить вычисления тогда и только тогда, когда компьютер не включен».

«Компьютер не может производить вычисления тогда и только тогда, когда компьютер включен».

5. Выражение A → B (читается: «если A, то B», «A влечет B») означает высказывание, которое ложно тогда и только тогда, когда A истинно, а B ложно. Такое высказывание называется импликацией (от лат. implico – «тесно связаны») высказываний A и B. Высказывание A называется условием или посылкой, высказывание B – заключением или следствием импликации. Иногда для A и B применяются термины антецедент («предшествующее») и консеквент («следствие»). Символ «→» (иногда символ É) обозначает операцию импликации.

Пусть ваш приятель пообещал вам: «Если завтра будет хорошая погода, то я приеду к тебе в гости». Данное высказывание является импликацией двух высказываний: A=«завтра будет хорошая погода» и B=«я приеду к тебе в гости». Мы расценим данную импликацию как ложь только в том случае, когда погода будет хорошая (A – истинно), но приятель к вам не приехал (B – ложно). В остальных случаях мы будем считать, что приятель не обманул, т.е. импликация истинна.

Также истинными высказываниями являются импликации «Если клятва дана, то она должна выполняться», «Если число делится на 9, то оно делится на 3», «Если выглянет солнце, то станет тепло».

В обычной речи связка «если...то» предполагает некую смысловую зависимость соединяемых высказываний. В алгебре логики для операции импликации смысловая связь несущественна. Так, например, высказывания «если 2*2=5, то трава синяя» и «если два больше трех, то восемь делится на четыре» являются истинными, так как у первого из них ложная посылка, а у второго – истинное следствие. Импликация «если 2*2=4, то 5<2» ложна, поскольку ее условие истинно, а заключение ложно.

Может показаться странным, что высказывание «Если А, то В» всегда истинно, если посылка (высказывание А) ложна. Но для математика это вполне естественно. В самом деле, исходя из ложной посылки, можно путем верных рассуждений получить как истинное, так и ложное утверждение.

Большинство математических теорем являются импликациями. Рассматривая некую теорему T как высказывание, можно придать ей вид импликации двух высказываний. Тогда высказывание A называют условием теоремы T, высказывание B – ее следствием. Или высказывание B называют необходимым условием для высказывания A, а высказывание A – достаточным условием для высказывания B в теореме T.

Примеры теорем: «Если две точки прямой принадлежат плоскости, то и вся прямая принадлежат плоскости», «Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны».

Пусть A, B, C – произвольные высказывания, которые рассматриваются как величины, принимающие одно из двух значений 0 или 1. Применяя к ним операции конъюнкции, дизъюнкции, импликации, эквивалентности и отрицания, можно получить новые сложные высказывания, например:

((AÚB)&)® .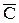

В обычной речи не всегда удается определить истинность или ложность сложного высказывания по истинности или ложности его составных частей. В алгебре высказываний значение сложного высказывания полностью определяется значениями его составляющих. Предположим, что A – ложное высказывание, B – истинное, C – ложное. Тогда высказывание

((AÚB)&)®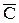

является ложным в силу определения логических операций.

Наряду с высказываниями, принимающими определенные и постоянные значения 0 и 1 и называемыми определенными высказываниями, в алгебре логики рассматривают переменные высказывания, которые не имеют фиксированного значения. Если X, Y, Z – переменные высказывания, то, применяя к ним операции конъюнкции, дизъюнкции, импликации, эквивалентности и отрицания, можно получить формулы алгебры логики. При некотором заданном значении переменных высказываний формула принимает определенное значение, которое может быть иным при иных значениях переменных высказываний. Таким образом, каждая формула определяет некоторую функцию, переменными которой являются переменные высказывания. Переменные и функции принимают только два значения: истина или ложь, поэтому функции можно описать конечной таблицей, которую называют таблицей истинности данной формулы.

Рассмотрим таблицы истинности для рассмотренных выше операций.

Таблица истинности для операции конъюнкции

x1	x2	y = x1&x2

Таблица истинности для операции дизъюнкции

x1	x2	y = x1Úx2

Таблица истинности для операции отрицания

x	y =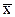

Таблица истинности для операции эквивалентности

x1	x2	y = x1~x2

Таблица истинности для операции импликации

x1	x2	y = x1®x2

Таблица истинности для функции y=((aÚb)&)®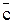

a	b	c	aÚb	(aÚb)&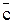		y

Возможен случай, когда две формулы имеют одну и ту же таблицу истинности. Такие формулы называются равносильными. При этом количество и состав переменных в формулах не обязательно должен совпадать. Так, например, равносильными являются формулы ((aÚb)&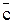)®и 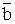Úс. Студентам предлагается убедиться в этом самостоятельно.

Запись формул можно упростить, опуская некоторые скобки и считая, что если их нет, то операции следует выполнять в следующем приоритетном порядке:

1. Отрицание.

2. Конъюнкция.

3. Дизъюнкция.

4. Импликация.

5. Эквивалентность.

Так, например, в выражении ((aÚb)&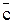)®можно убрать внешние скобки, поскольку приоритет операции & выше, чем операции ®. В результате получим равносильное выражение (aÚb)&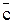®. Заметим, что оставшиеся скобки убраны быть не могут, поскольку в этом случае формула будет иметь по сути следующий вид: aÚ(b&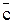)®, что не равносильно первоначальной формуле.

Если все значения формулы в таблице истинности при любых значениях аргументов равны единице (нулю), то формула называется тождественно истинной (ложной) или тавтологией. Тавтологию следует понимать так: какие бы значения аргументов формулы мы не задали, результатом все равно будет одно и то же значение. С математической точки зрения формулы-тавтологии называют «константа 1» (или «константа 0», если все значения формулы равны нулю).

Примеры формул-тавтологий:

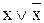
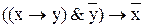
Студентам предлагается самостоятельно доказать тавтологичность данных формул с помощью таблиц истинности.

Лекция 10

Дата добавления: 2014-01-06