С помощью аналитических преобразований

Минимизация булевых функций

Используя законы булевой алгебры, можно получить для одной и той же логической функции множество эквивалентных представлений. Чем проще аналитическое выражение функции, тем экономичнее и проще ее практическая реализация в виде программного кода или электронных схем. Процесс преобразования логической функции к минимальному виду аналитической записи называется минимизацией логической функции.

Рассмотрим несколько примеров, поясняющих процесс минимизации.

Пример 1. Пусть задана следующая булева функция:

.

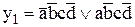В силу дистрибутивного закона (теорема T₁₄) сгруппируем данные термы и вынесем за скобки общую часть . В скобках останется выражение (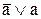), которое в силу свойства идемпотентности (теорема T₅) равно единице при любом значении переменной a. В силу свойства идентичности (теорема T₂) выражение , «умноженное» на единицу, останется неизменным. Если все сказанное записать математически, получим следующее:

.

Как показывает данная запись, выражение полностью эквивалентно выражению . При этом выражение содержит три переменных вместо четырех и две логические операции (не считая инверсий) вместо семи, и является минимально возможным для функции y₁, то есть не поддается дальнейшей минимизации.

В данном примере процесс минимизации, основываясь на ряде законов алгебры логики, позволил заметно упростить исходное выражение, не изменив саму функцию (ее таблицу истинности). Переменная a была удалена из выражения как несущественная (фиктивная). Фактически, мы здесь применили правило склеивания (теорема T₁₈), которое наиболее часто применяется в процессе минимизации.

Выражение, полученное в результате, называется минимальной дизъюнктивной нормальной формой (МДНФ) и дальнейшей минимизации не подлежит.

Пример 2. Пусть задана следующая булева функция:

.

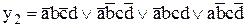В силу закона ассоциативности (T₁₀) сгруппируем первый терм с третьим, а второй – с четвертым, заключив полученные группы в скобки. С каждой скобкой поступим аналогично примеру 1. Получим следующее:

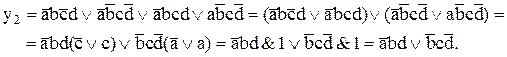
Таким образом, за счет использования законов алгебры логики нам удалось уменьшить как количество термов, так и их размер, что в итоге сократило количество логических операций (не считая инверсий) с 15 до 5. Составив таблицы истинности для исходного и конечного выражений, можно убедиться, что они полностью эквивалентны.

Дальнейшая минимизация полученного выражения невозможна, следовательно, мы получили МДНФ.

Пример 3. Пусть булева функция задана следующим выражением:

.

В силу закона идемпотентности (T₅) запишем первый терм два раза (при этом функция y₃ не изменится). Затем выполним группировку первого терма со вторым и копии первого терма с третьим:

Рассмотрим важный момент. В полученном нами результирующем выражении оба терма имеют общую часть , которую можно вынести за скобки: . Важно понимать, что само по себе вынесение за скобки минимизацией не является – это обычная перегруппировка. Процесса поглощения (уничтожения) какой-либо переменной не происходит, хотя операций становится на одну меньше. Если скобки раскрыть, то мы снова получим исходное выражение. Таким образом, выражение дальнейшей минимизации не подлежит и представляет собой минимальную ДНФ для функции y₃.

Пример 4. Пусть булева функция задана следующим выражением:

,

где y₃ – выражение из предыдущего примера.

Сопоставляя терм 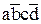с первыми тремя термами, можно убедиться, что никакая группировка не приведет к упрощению терма 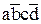, поскольку данный терм не имеет трех общих переменных (которые можно вынести за скобки) ни с одним другим термом. Это означает, что в данном конкретном примере мы ничего не можем сделать с термом 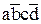и вынуждены оставить его без изменений. Выполнив над первыми тремя термами все действия, рассмотренные в предыдущем примере, мы получим для функции y₄ следующую МДНФ:

.

Не смотря на то, что терм 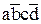оказался «бесполезен», мы все же провели минимизацию с использованием оставшихся термов и упростили исходное выражение.

Следует понимать, что в процессе преобразования мы не имеем права выполнять какие-либо действия, приводящие к изменению исходной функции. Например, если бы мы просто выбросили терм 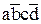из исходного выражения, то у нас была бы уже не исходная функция, а какая-то другая, что недопустимо.

Пример 5. Пусть булева функция задана следующим выражением:

.

Сгруппируем первый терм с четвертым, а второй – с третьим:

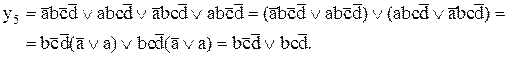
Заметим, что полученное выражение может быть подвергнуто дальнейшей минимизации путем вынесения общей части за скобки:

.

Таким образом, за счет двукратного применения правила склеивания, мы «поглотили» две переменных: сначала a, затем c. Обе этих переменных оказались несущественными. Результирующее выражение содержит единственный терм, состоящий из двух переменных, вместо четырех термов, состоящих из четырех переменных. При всем при этом исходное выражение 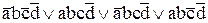и результирующее выражение полностью эквивалентны.

Пример 6. Пусть задана следующая булева функция:

.

Заранее нужно сказать, что все последующие действия хотя и не представляют особой сложности, но совершенно не являются очевидными при взгляде на функцию y₆. Если при подготовке данного лекционного материала все действия были заранее продуманы и проверены, то столкнувшись с необходимостью аналитической минимизации подобного выражения без предварительной подготовки, можно потратить достаточно много времени, прежде чем найти подходящее решение. Мы же рассмотрим краткое, заранее подготовленное описание требуемых действий.

Итак, продублируем термы №3 и №4, в результате чего получим соответственно термы №7 и №8. Сгруппируем термы следующим образом:

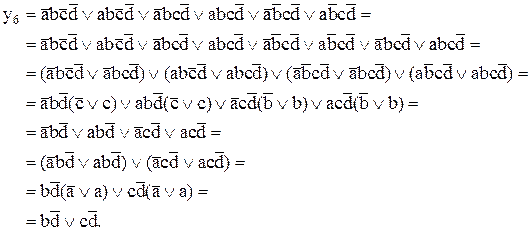
Таким образом, в результате применения ряда законов алгебры логики мы упростили исходное выражение, получив для него минимальную ДНФ.

Пример 7. Пусть булева функция четырех переменных задана следующей таблицей истинности:

a b c d	y7
0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1	*
1 0 1 0
1 0 1 1
1 1 0 0
1 1 0 1
1 1 1 0
1 1 1 1

Заметим, что таблица истинности содержит строку, в которой функция принимает значение, равное «*». Звездочка означает, что при данном наборе входных переменных наша функция не определена, то есть может принимать любое значение – ноль или единицу. На практике считается, что наборы переменных, при которых функция равна *, никогда не возникнут, поэтому значение функции на данных наборах не имеет значения и может быть любым. В обычной математике подобной ситуации соответствует, например, функция логарифма при x<0. Если при x=0 функция log(x) = – ¥, то при x<0 она вообще не существует (не определена) и неизвестно чему равна.

Звездочек может быть больше одной (вплоть до того, что вся таблица истинности заполнена звездочками). Пока в таблице присутствуют звездочки, функция считается не полностью определенной. Для практического использования ее нужно доопределить, то есть заменить звездочки на нули или единицы. Поскольку в нашем примере звездочка может быть заменена на 0 или 1, мы имеем два варианта замены:

1) y₇(1001) = 0;

2) y₇(1001) = 1.

К слову говоря, при наличии в таблице истинности двух звездочек у нас было бы четыре варианта замены (00, 01, 10, 11), при трех звездочках – 8 вариантов, при четырех звездочках – 16 вариантов, при 12 звездочках –
2¹² = 4096 вариантов и т.д.

Какой же вариант выбрать? Обычно выбирают такой вариант замены, который приводит к минимально возможной ДНФ.

Допустим, мы заменили звездочку нулем. В этом случае таблица истинности будет содержать одну единичную строку, и ее ДНФ, являющаяся также и МДНФ, будет иметь вид:

.

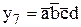Допустим, мы заменили звездочку единицей. В этом случае СДНФ будет содержать два терма, которые (оказывается) могут быть склеены:

.

Таким образом, несмотря на то, что СДНФ у нас увеличивается, дополнительная единица дает возможность минимизации функции и позволяет получить более короткую запись МДНФ.

Однако замена звездочки на единицу полезна не всегда. Если бы в нашем примере звездочка стояла не в строке 1001, а в строке 1010, то при замене ее на единицу мы получили бы терм , который не может быть склеен с «обязательным» термом . В результате мы бы только усложнили функцию, добавив туда лишний терм, который можно и не добавлять при замене звездочки нулем.

Пример 8. Пусть булева функция четырех переменных задана следующей таблицей истинности:

a b c d	y8
0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
0 1 0 1
0 1 1 0	*
0 1 1 1
1 0 0 0
1 0 0 1
1 0 1 0
1 0 1 1
1 1 0 0
1 1 0 1	*
1 1 1 0
1 1 1 1

Попробуем проанализировать, какая из звездочек может быть нам полезна или бесполезна. В таблице есть единственная строка, равная единице, которая дает нам «обязательный» терм . Первая звездочка может дать терм , который склеивается с термом и поэтому является полезным. Вторая звездочка может дать терм , который с термом не склеивается, и поэтому является с точки зрения минимизации бесполезным. Таким образом, первую звездочку заменяем на единицу (говорят – доопределяем единицей), вторую доопределяем нулем. В результате получаем следующую МДНФ:

.

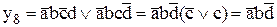Пример 9. Пусть булева функция четырех переменных задана следующей таблицей истинности.

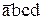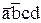В таблице есть две строки, в которых функция равна единице. Эти единицы дают нам два «обязательных» терма: и . Первая звездочка может дать терм , который склеивается с термом 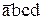и поэтому является полезным. Вторая звездочка может дать терм 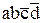, который склеивается с термом и поэтому является полезным. Третья звездочка может дать терм 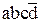, который не склеивается ни с одним термом и поэтому является бесполезным. Таким образом, звездочки в строках 0011 и 1100 доопределяем единицами, а звездочку в строке 1110 – нулем.

a b c d	y9
0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1	*
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1
1 0 1 0
1 0 1 1
1 1 0 0	*
1 1 0 1
1 1 1 0	*
1 1 1 1

После доопределения звездочек получим следующий результат:

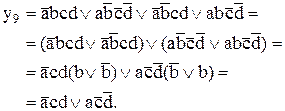
Конечное выражение 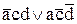не может быть упрощено и поэтому является минимальной ДНФ для функции y₉.

Пример 10. В данном примере мы рассмотрим достаточно сложную функцию, таблица истинности которой содержит множество единиц, нулей и звездочек. Для того, чтобы найти минимальную ДНФ, требуется достаточно много времени (несколько часов). При этом можно пойти различными путями и даже найти несколько различных по виду, но эквивалентных МДНФ. Разумеется, в рамках лекции мы рассмотрим лишь одно из возможных решений, причем не сам ход мыслей, а готовый результат.

Пусть булева функция от пяти (!) переменных задана своей таблицей истинности. Для экономии места на бумаге столбец из 32 строк разбит на два столбца по 16 строк.

a b c d e	y10		a b c d e	y10
0 0 0 0 0			1 0 0 0 0	*
0 0 0 0 1			1 0 0 0 1
0 0 0 1 0			1 0 0 1 0	*
0 0 0 1 1			1 0 0 1 1
0 0 1 0 0			1 0 1 0 0	*
0 0 1 0 1			1 0 1 0 1
0 0 1 1 0	*		1 0 1 1 0
0 0 1 1 1			1 0 1 1 1
0 1 0 0 0			1 1 0 0 0
0 1 0 0 1			1 1 0 0 1
0 1 0 1 0	*		1 1 0 1 0
0 1 0 1 1	*		1 1 0 1 1	*
0 1 1 0 0			1 1 1 0 0
0 1 1 0 1	*		1 1 1 0 1
0 1 1 1 0			1 1 1 1 0
0 1 1 1 1	*		1 1 1 1 1

Доопределим функцию так, как показано в следующей таблице. В рамках лекции мы не будем рассматривать, почему мы доопределяем функцию именно так, но студент должен понимать, что такому доопределению предшествует длительный процесс анализа. Строки, которые мы доопределили, для наглядности показаны на сером фоне.

a b c d e	y10		a b c d e	y10
0 0 0 0 0			1 0 0 0 0
0 0 0 0 1			1 0 0 0 1
0 0 0 1 0			1 0 0 1 0
0 0 0 1 1			1 0 0 1 1
0 0 1 0 0			1 0 1 0 0
0 0 1 0 1			1 0 1 0 1
0 0 1 1 0			1 0 1 1 0
0 0 1 1 1			1 0 1 1 1
0 1 0 0 0			1 1 0 0 0
0 1 0 0 1			1 1 0 0 1
0 1 0 1 0			1 1 0 1 0
0 1 0 1 1			1 1 0 1 1
0 1 1 0 0			1 1 1 0 0
0 1 1 0 1			1 1 1 0 1
0 1 1 1 0			1 1 1 1 0
0 1 1 1 1			1 1 1 1 1

Для удобства выпишем отдельно все минтермы, которые есть в таблице истинности. Минтермы обозначим символами Q_i.

Q₁ = 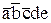; Q₆ = ;

Q₂ = 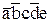; Q₇ = ;

Q₃ = 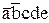; Q₈ = ;

Q₄ = 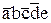; Q₉ = ;

Q₅ = 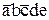; Q₁₀ = .

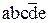В силу теоремы T₅ любой терм мы можем дублировать сколько угодно раз. С учетом этого представим нашу СДНФ следующим образом:

y₁₀ = (Q₁ÚQ₅ÚQ₈ÚQ₉) Ú(Q₄ÚQ₅ÚQ₆ÚQ₇) Ú(Q₂ÚQ₃ÚQ₆ÚQ₇) Ú(Q₆ÚQ₁₀).

Таким образом, нам потребовалось по две копии термов Q₅ и Q₇, и три копии терма Q₆.

Выполним преобразования выражений в скобках.

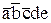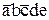Q₁ÚQ₅ÚQ₈ÚQ₉ = ÚÚÚ=

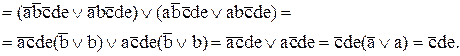
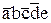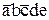Q₄ÚQ₅ÚQ₆ÚQ₇ = Ú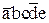ÚÚ=

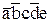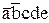Q₂ÚQ₃ÚQ₆ÚQ₇ = Ú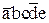ÚÚ=

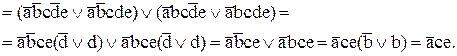
Q₆ÚQ₁₀ = Ú=() = .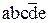

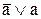Таким образом, получаем следующую МДНФ:

y₁₀ = 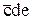ÚÚÚ.

Дата добавления: 2014-01-06