Непериодические сигналы

Спектр

Совокупности коэффициентов a_k, b_k, k=1, 2, 3,…, разложения периодической функции x(t) в ряд Фурье называется частотными спектрами этой функции Совокупность амплитуд и соответствующих частот гармоник принято называть спектром амплитуд.

Совокупность амплитуд и соответствующих частот гармоник называется спектром фаз.

Спектр амплитуд и спектр фаз однозначно определяют сигнал. Однако для многих практических задач достаточно ограничиться спектром амплитуд.

Рисунок 4.2 - Спектр амплитуд и спектр фаз

Характерной особенностью спектра периодического сигнала является его прерывистость (дискретность). Расстояние между соседними спектральными линиями одинаковое и равно частоте основной гармоники.

Всякий непериодический сигнал можно рассматривать как периодический, период изменения которого равен ¥. В связи с этим спектральный анализ периодических процессов может быть обобщен и на непериодический сигнал.

Рисунок 4.3 - Непериодический сигнал

Любой физически реализуемый сигнал с конечной энергией обязательно ограничен во времени, или, иными словами, функция, изображающая такой сигнал, абсолютно интегрируема. В связи с этим непериодический сигнал может быть выражен модифицированной формулой периодического сигнала.

Модификация заключается в приравнивании периода колебаний Т бесконечности и следующих из этого математических преобразований. Подставляя в комплексную форму ряда Фурье функции 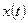выражение комплексной амплитуды 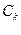, получим:

,

где

Для непериодической функции , следовательно, частотный интервал между соседними гармониками . В этом выражении деление на бесконечно большой период Т может быть заменено умножением на бесконечно малое приращение частоты , что в свою очередь, превращает процесс суммирования в интегрирование, а произведение 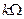в текущую частоту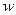

то есть:

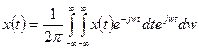
(2.3)

Это выражение известно как двойной интеграл Фурье, а величина

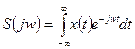
(2.4)

называется прямым преобразованием Фурье функции 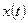. Эта величина характеризует спектральный состав непериодической функции 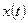и может быть названа спектральной плотностью или спектральной характеристикой функции .

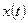Выражение

(2.5)

представляющее зависимость непериодической функции от её спектральной характеристики, называется обратным преобразованием Фурье.

Здесь:

- спектральная плотность;

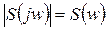- амплитудно-частотная характеристика сигнала;

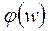- фазо-частотная характеристика сигнала.

Представление непериодической функции интегралом Фурье возможно при выполнении следующих условий:

функция 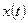удовлетворяет условиям Дирихле

функция 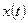абсолютно интегрируема, т.е.

(2.6)

(этим условиям удовлетворяет практически любой реальный сигнал).

Огибающая спектра (модуль спектральной плотности) непериодической функции (сигнала) имеет непрерывный характер.

Т.е. спектр непериодического сигнала в отличие от спектра периодического сигнала является сплошным. Спектральная плотность однозначно отображает непериодический сигнал и удовлетворяет условиям:

;

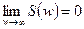Модуль спектральной плотности является четной, а аргумент – нечетной функцией частоты, т.е.

,

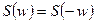(2.7)

Пример

Рассмотрим спектр периодического сигнала на примере амплитудно-модулированного гармонического сигнала.

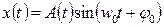
(2.8)

При амплитудной модуляции амплитуда изменяется по определенному закону:

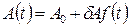
(2.9)

где А₀ – постоянная составляющая амплитуду,

dА – наибольшее изменение амплитуды при модуляции,

f(t) – нормированная функция (изменяется в пределах от –1 до +1)

Так как модулируемый параметр сигнала (в данном случае амплитуда) является непосредственным переносчиком, то функция f(t) выражает закон изменения во времени передаваемого сообщения. Амплитудно-модулированный гармонический сигнал как функция времени в общем случае имеет вид:

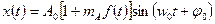
(2.10)

где - глубина амплитудной модуляции.

Рассмотрим частный случай, когда функция f(t) изменяется по гармоническому закону

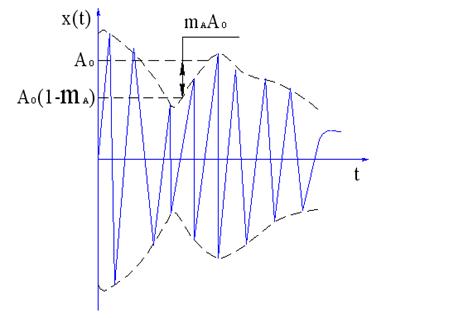
Рисунок 4.4 График изменения функции f(t)

, причем

Тогда выражение (

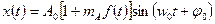
(2.10)

) примет вид

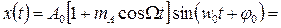
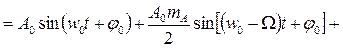
(2.11)

Рисунок 4.5 Спектр сигнала

То есть спектр сигнала, изображенного на рисунке, состоит из трех гармонических составляющих: несущей с частотой и двух боковых:

нижней с частотой

верхней с частотой .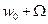

Ширина спектра сигнала .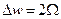

Как мы видим, в данном случае для нахождения частотной модели не потребовалось использование аппарата Фурье, поскольку другой путь поиска амплитудно-частотной характеристики напрашивается сам по себе и он довольно простой и быстрый.

Дата добавления: 2014-01-06