Градиентный метод

Одним из методов нелинейного программирования является градиентный метод. Он применим при любом виде уравнений ограничения и минимизируемой функции, если эта функция дифференцируема, а также дифференцируемы зависимые переменные.

В теории оптимизации градиентный метод называется также методом «скорейшего спуска», если он используется для поиска минимального значения целевой функции.

Если необходимо отыскать максимальное значение целевой функции, применяется другая модификация градиентного метода, которая получила наименование «метода крутого восхождения».

Необходимое условие минимума функции F(X) состоит в равенстве нулю всех частных производных по независимым переменным:

где X – вектор m переменных (компонентами вектора являются как зависимые, так и независимые переменные);

n – число независимых переменных.

Градиентом функции F(X) называют вектор, i- я компонента которого равна частной производной ,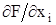

где x_i – независимая переменная.

Необходимое условие минимума записывается следующим образом:

| grad _xF|

где e - заданная малая величина.

Пусть требуется минимизировать функцию

при наличии k уравнений ограничений (k<m):

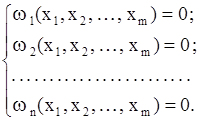
Произвольно выбираем k зависимых и n независимых переменных (n =m −k).

Задаёмся произвольными значениями независимых переменных и определяем значения зависимых переменных и всех частных производных Z по независимым переменным:

Для определения частных производных по независимым переменным могут использоваться следующие уравнения:

i = 1, 2,..., n; j = n+1, n+2, …, m,

где 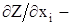полные частные производные от функции Z, определяемые при неизменности остальных независимых переменных, но при изменениях зависимых переменных;

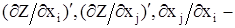частные производные, определяемые при неизменности всех остальных переменных (как зависимых, так и независимых).

Если все производные (13) имеют значения, не превышающие допустимой погрешности расчетов, то получено оптимальное решение. В противном случае корректируются значения всех независимых переменных и производится следующая итерация расчёта.

Итерационный процесс повторяется до тех пор, пока значение модуля градиента не станет меньше некоторой достаточно малой величины e:

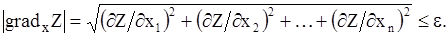(54)

Переход от i -го к (i+ 1)-му приближению осуществляется по направлению,

обратному градиенту (по антиградиенту), по выражениям:

В этих выражениях t – шаг по направлению антиградиента.

Различные модификации градиентного метода отличаются способом выбора шага t, который очень сильно влияет на сходимость. В настоящее время разработано значительное количество аналитических способов выбора оптимального или близкого к нему шага. Оптимальный шаг соответствует наибольшему изменению целевой функции и обеспечивает быструю сходимость итерационного процесса.

Применение градиентного метода значительно усложняется, если ограничения заданы в форме неравенств. В этом случае движение по антиградиенту допускается только при соблюдении всех ограничений. При выходе за границу области ограничений движение производится по проекции антиградиента на границу этой области.

Для определения глобального минимума требуется не только выпуклость целевой функции, но и выпуклость области ограничений.

Основное достоинство градиентного метода состоит в том, что его сходимость мало зависит от выбора начального приближения, т.е. близости начального приближения к решению. Этот позволяет использовать градиентный метод также для приближённого решения систем нелинейных уравнений в тех случаях, когда с помощью других методов это решение получить невозможно.

Дата добавления: 2014-01-06