Численные методы решения нелинейных дифференциальных уравнений

Критерий устойчивости Рауса

Критерий Рауса основан на составлении таблиц особого вида, в которой используются коэффициенты характеристического уравнения.

Элементами первой строки этой таблицы служат коэффициенты с четными индексами (начиная с нулевого), элементами второй строки – с нечетными индексами. Элементы третьей строки получаются из элементов первой вычитанием из нее второй строки, умноженной на А₀ /А₁, и сдвигом на один столбец влево. Элементы каждой следующей строки образуются таким же способом из двух

предыдущих строк.

Таблица Рауса

Номер строки	Номер столбца
	А0	А2	А4	А6
	А1	А3	А5	А7
	А13=А2 -А3×А0/А1	А23=А4 -А5×А0/А1	А33=А6 -А7×А0/А1	…
	А14=А3 -А23×А1/А13	А24=А5 -А33×А1/А13	А34=А7 -А43×А1/А13	…
	А15=А23 -А24×А13/А14	................	................	…

Для того чтобы действительная часть всех корней характеристического уравнения была отрицательной, необходимо и достаточно, чтобы все элементы первого столбца таблицы Рауса были отличны от нуля и имели один и тот же знак.

При определении переходных процессов в электрических системах необходимо решать системы обыкновенных дифференциальных уравнений. В большинстве случаев эти уравнения нелинейны.

Задачу изучения переходных процессов целесообразно разбить на два этапа.

На первом этапе изучаются переходные процессы статически устойчивой системы при малых возмущениях.

На втором этапе изучаются переходные процессы после больших возмущений, когда нелинейные свойства системы могут качественно менять характер переходного процесса.

Иногда по условиям задачи для анализа динамической устойчивости может быть выбрана линейная модель, однако ее порядок высок. Поэтому более эффек-

тивными оказываются численные методы решения.

Рассмотрим общий подход к решению дифференциальных уравнений на примере уравнения первого порядка:

(64)

Заменим в этом уравнении производную отношением конечных малых приращений Dx и Dt:

Dx/Dt = f(t, x),

откуда

Dx = f(t, x)× Dt.

Как известно, общим решением уравнения (64) называется решение, содержащее постоянную интегрирования и содержащее все частные решения исходного уравнения. Очевидно, что подобное решение численными методами получить нельзя. Они используются для нахождения частного решения, удовлетворяющего заданным начальным условиям:

t = t₀; x(t₀) = x₀

Зная начальные условия интегрирования, запишем приращение искомой функции на первом шаге в следующем виде:

Dx₁ = f(t₀ , x₀)× Dt,

откуда получаем значение функции после первого шага

x₁ = x₀ + f(t₀ , x₀)× Dt.

Полученное значение x ₁ соответствует времени

t₁ = t₀ + Dt.

Аналогично получаем значение x₂ и t₂:

x₂ = x₁ + f(t₁ , x₁)× Dt;

t₂ = t₁ + Dt.

Отмечая индексом k значения переменных на k-м шаге интегрирования, получаем: x_k+1 = x_k + f(t_k, x_k)× Dt

Таким образом, численное решение дифференциального уравнения сводится к

замене реальной интегральной кривой конечным числом прямоугольных отрезков. При этом возникают ошибки двух видов: локальная ошибка (ошибка данного шага) и накапливаемая за время интегрирования ошибка.

Наличие этих ошибок может приводить в некоторых случаях к совершенно неприемлемым результатам расчетов. Для их уменьшения есть только один путь - уменьшение шага интегрирования, что приводит к увеличению длительности расчетов

Описанный выше метод называется методом Эйлера.

При необходимости получения более точного результата при том же шаге используют другие, более точные методы расчета.

Если функции x(t) в окрестности точки t достаточное число раз дифферен

цируема то для нахождения ее значения при t+Dt можно воспользоваться разложением Тейлора.

В современных математических пакетах наиболее часто используется метод Рунге-Кутта четвертого порядка.

Основная схема этого метода имеет вид:

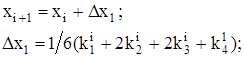
где

Решение дифференциальных уравнений численными методами рекомендуется производить с помощью математических пакетов программ. Эти программы позволяют получить решение как в аналитическом, так и графическом виде.

Наиболее известными сегодня являются следующие пакеты:, Matlab (фирма The MathWorks), MathCad (фирма MathSoft inc.), Maple (фирма Waterloo Maple inc.), Mathematica (фирма Wolfram Research).

В инженерной практике наиболее популярен пакет MathCad, который в отличие от упомянутых выше пакетов является средой визуального программирования, т.е. не требует знания специфического набора команд. Характерной особенностью пакета является использование стандартных математических обозначений, т.е. документ на экране выглядит точно так же, как обычный математический расчет.

Системы дифференциальных уравнений для их решения в среде Mathcad до­лжны быть представлены в форме Коши, т.е. должны быть заданы начальные значения переменных, а дифференциальные уравнения разрешены относительно

производных.

Для решения поставленной задачи может быть использована следующая функция системы MathCAD:

rkfixed(X,t_H,Dt,n,f),

где X – вектор начальных значений параметров;

t_H – начальное значение независимой переменной (обычно независимой пе-

ременной является время, отсчитываемое от начала переходного процесса);

Dt – шаг вычислений (диапазон изменения времени на каждом шаге), с;

n – число шагов;

f – вектор производных.

Вектор производных должен быть задан в символьной форме, т.е. в виде

формул. Элементами вектора X являются численные значения.

Функция Rkadapt благодаря автоматическому изменению шага решения дает более результат, однако по скорости вычисления она проигрывает функции

rkfixed.

Для того чтобы назначить величину шага, обеспечивающую необходимую точность вычислений, расчет повторяют при шаге, в два раза меньшем первоначального. Если разница в результатах вычислений превышает требуемую точ-

ность, то шаг разбиения уменьшается и расчет повторяется.

Дата добавления: 2014-01-06