Регрессионный анализ

В энергетике случайные величины, как правило, являются зависимыми, причем определение одной из них более доступно, чем другой, от нее зависящей. Зависимость двух случайных величин отличается от обычного понимания функциональной зависимости неслучайных величин.

Будем считать независимой переменной x, а зависимой – y.

При функциональной зависимости каждому значению аргумента соответствует единственное значение функции.

Если величины связаны между собой случайной зависимостью, то, зная значение x, нельзя точно указать значение y, а можно указать только её закон распределения, зависящий от того, какое значение приняла величина x.

Вероятностная зависимость может быть более или менее тесной; по мере увеличения тесноты вероятностной зависимости она все более приближается к функциональной. Функциональную зависимость можно рассматривать как крайний, предельный случай наиболее тесной вероятностной зависимости. Другой крайний случай – полная независимость случайных величин. Между этими двумя крайними случаями лежат все градации вероятностной зависимости – от самой сильной до самой слабой. Те физические зависимости, которые на практике считаются зависимыми, в действительности связаны весьма тесной вероятностной зависимостью.

Таким образом, величина y состоит из двух составляющих: функциональной зависимости f(x) и случайной составляющей e:

y = f(x)+e

Из этого уравнения следует, что каждому значению х соответствует определенное математическое ожидание = f(x).

Последнее уравнение называется уравнением регрессии. Для упрощения записи вместо применяется обычное обозначение переменной y.

Задача регрессионного анализа – выбор вида уравнения регрессии и оценка параметров регрессии. Вид функции должен быть по возможности прост, но в то же время хорошо отражать реальную зависимость. Выбор вида функции базируется на физических предпосылках, материалах решения аналогичных задач и т.д.

Если вид функции заранее не известен, то первым шагом определения этой функции является нанесение экспериментальных точек на график. В результате будет получена диаграмма разброса, из которой часто удается визуально найти плавную кривую и определить соответствующую ей зависимость.

Расчет параметров регрессии производится по методу наименьших квадратов, согласно которому для наилучшего приближения экспериментальных данных к теоретическим, необходимо, чтобы сумма квадратов отклонений результатов экспериментов от значений y, вычисленных по уравнению регрессии, была минимальной.

Если зависимость между случайными величинами выражается уравнением регрессии y=ax+b, то имеет место простая линейная регрессия, где a и b – параметры регрессии.

Пример 11. Подобрать уравнениерегрессиипо экспериментальным данным, приведенным в таблице 12.

Таблица 12

x		0,5		1,5
y	7,0	4,8	2,8	1,4

Р е ш е н и е. Выбираем уравнение регрессии вида y = a +bx.

Для расчета параметров регрессии предварительно заполним таблицу 13. В таблице предусмотрен дополнительный столбец y_i², который в дальнейшем будет необходим для расчета коэффициента корреляции.

Таблица 13

xi	xi^2	yi	xi×yi	yi^2
0,5 1,0 1,5	0,25 1,0 2,25	7,0 4,8 2,8 1,4	2,4 2,8 2,1	23,04 7,84 1,96
åxi = 5	åxi^2 = 7,5	åy = 16	åxi×yi = 7,3	åyi^2 = 81,84

Составим систему уравнений:

.

Подставим табличные значения (см. табл.13):

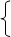a×5 + b×5 = 16;

a×5 + b×7,5 = 7,3.

Вычитая из первого уравнения второе, получаем:

-2,5×b = 8,7

b = -8,7/2,5=-3,48; a = (16 + 5× 3,48)/5 = 6,68.

Следовательно, уравнение регрессии имеет следующий вид:

y = 6,68 - 3,48 x

Дата добавления: 2014-01-06