Лекция 4. 4.1. Ошибки при передаче информации

4.1. Ошибки при передаче информации.

Количество искаженных символов кодовой последовательности называется кратностью ошибки.

При взаимно независимых ошибках вероятность искажения любых r символов в n- разрядной кодовой комбинации равна:

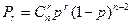(1.11.11)

Как уже отмечалось при d = 1 все кодовые комбинации информационные, т.е. разрешенные и такой код не обладает корректирующей способностью.

А уже при d = 2, т.е. для n = 3 имеем

000; 011; 101; 110 разрешенные

001; 010; 100; 111 неразрешенные кодовые комбинации (по четному признаку).

Для однократных ошибок ни одна из разрешенных комбинаций не может трансформироваться в другую разрешенную, т.е. код может обнаруживать одиночные ошибки. В общем случае при необходимости обнаруживать ошибки кратности r минимальное кодовое расстояние, должно быть

d_min ≥2+1 (1.11.12)

Для исправления одиночной ошибки каждой разрешенной комбинации необходимо сопоставить свое подмножество запрещенных комбинаций.

Чтобы эти подмножества не пересекались, кодовое расстояние между разрешенными комбинациями должно быть не меньше трех (3). Для данного кода. Так при n = 3 при разрешенной кодовой комбинации 000 подмножество запрещенных кодовых комбинаций для обнаружения одиночной ошибки будет:

001; 010; 100

В общем случае для исправления ошибок кратности s минимальное кодовое расстояние между разрешенными кодовыми комбинациями должно удовлетворять соотношению:

d_min ≥2s+1 (1.11.13)

где s – число ошибок, исправляемых кодом.

Или для обнаружения всех ошибок кратности s и кратности r необходимо:

d_min ≥2+s+1 (1.11.14)

Одной из основных характеристик корректирующего кода является избыточность кода, указывающая степень удлинения кодовой комбинации для достижения определенной корректирующей способности.

Если на каждые n символов выходной последовательности приходится k информационных и (n – k) - проверочных, то относительная избыточность будет:

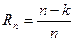(1.11.15)

или

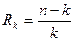(1.11.16)

Величина 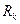является предпочтительнее.

Коды, обеспечивающие заданную корректирующую способность при минимально возможной избыточности, называются оптимальными (или плотноупакованными).

В связи с нахождением оптимальных кодов, найдем число Q разрешенных комбинаций n - значного двоичного кода, обладающего способностью исправлять взаимно независимые ошибки кратности s. Это равносильно отысканию числа комбинаций, кодовое расстояние между которыми не менее d=2s+1 (см. формулу 1.11.13).

Общее число различных исправляемых ошибок для каждой разрешенной комбинации составляет:

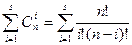
Каждая из таких ошибок должна приводить к запрещенной комбинации, относящейся к подмножеству данной разрешенной комбинации. Совместно с этой комбинацией подмножество включает 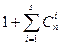комбинаций.

Хемминг показал, что однозначное декодирование с корректированием, возможно только в случае, когда названные подмножества не пресекаются.

Число разрешенных комбинаций:

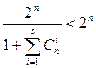или 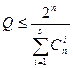(1.11.17)

В качестве примера рассмотрим семиэлементный код Хемминга: n =7, n₀ =4, k=3.

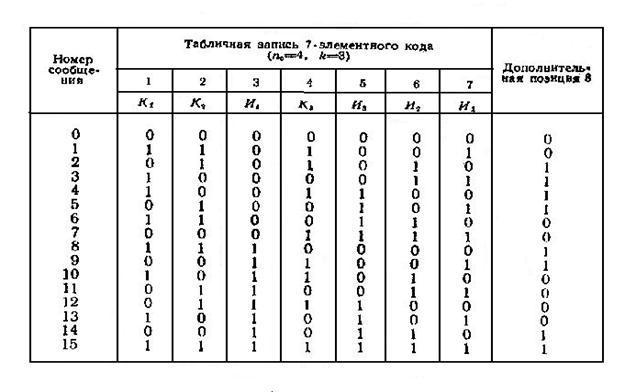Таблица 1.

Здесь n – общее число символов (элементов) кода; n₀- число информационных элементов, образующих последовательность двоичных чисел; k – число проверочных (контрольных) элементов, которые вводятся так, чтобы в табличной записи кодовой комбинации в результате определенного ряда проверок в данной строке на четность (суммированием по модулю 2) можно было определить место и исправить искаженный элемент в строке принятой комбинации кода.

Проверки на четность производятся в соответствии с закономерностями построения таблицы двоичных чисел, и в результате записывается «0» при отсутствии ошибок и «1» при обнаружении ошибок, т.е. в виде двоичного числа. Всего производится k проверок по числу контрольных элементов и записывается k-разрядное двоичное число, которое определяет номер позиции кода с ошибкой. Контрольные элементы принято размещать на позициях 2⁰, 2¹, 2², …,2^k-1, т.е. на позициях 1, 2, 4, 8, 16,…(в десятичной записи). При этом контрольные элементы записываются на позициях кода, начиная с крайней левой, первой позиции. Младший информационный разряд, соответствующий 2⁰, записывается на правой позиции, следующий информационный разряд левее и т.д.

Информационные коды размещены на позициях 3, 5, 6, 7, контрольные элементы на позициях 1, 2, 4. Дополнительная восьмая позиция введена для проверки для проверки на общую четность, поэтому кодовое расстояние d_min =3+1=4.

В коде Хемминга на каждой горизонтальной строке размещено четыре единицы (за исключением 0 и 15^ой), что позволяет увеличить защищенность кода путем счета единиц.

Определение местоположения ошибки состоит в следующем:

Допустим, принята искаженная комбинация 0111000 (без позиции 8, но позиция 8=0). Такая комбинация отсутствует в таблице.

Проверим на четность соответствующие разряды кодовой комбинации. При первой проверке (а всего проверок 3, k=3) суммируются единицы по модулю 2 на 1, 3, 5 и 7 позициях кода. В проверяемой строке такое суммирование дает «1», которая и записывается на позиции 1 кода. Вторая проверка охватывает позиции 2, 3, 6, 7. В результате суммирования получаем «0», который записывается на второй позиции кода. При проверке 3 на позициях 4, 5, 6 и 7 получаем «1», которую записывается в третьем разряде.

В результате получили проверочное число 101, которое соответствует десятичному числу 5, указывающему на искажение кода в пятой позиции. При изменении на этой позиции 0 на 1 восстанавливается разрешенная кодовая комбинация 0111100, т.е. число 12. Такое исправление на приемной стороне производится автоматически. Дополнительная позиция 8 увеличивает кодовое расстояние d_min =2+1+1=4 и позволяет исправлять одну (s=1) и обнаруживать 2 (r = 2) ошибки. Избыточность кода

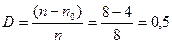или 50%

Выбор числа контрольных элементов k в коде Хемминга при заданном числе информационных символов n₀ производится по выражению:

n+ 1 = n₀+k + 1 ≤ 2^k (1.11.18)

Циклические коды широко применяют при передаче данных и в современных системах телемеханики благодаря их высокой эффективности. Они требуют сравнительно небольшой избыточности и отличаются простотой реализации кодирующих и декодирующих устройств на регистрах сдвига с обратными связями, включенными через сумматоры по модулю 2. Циклические коды могут обнаруживать и исправлять от одной до нескольких ошибок в кодовой комбинации, в зависимости от выбранной избыточности. Они, так же как и код Хемминга, относятся к блочным, систематическим кодам, у которых каждая кодовая комбинация кодируется и декодируется (блочные коды) и состоит из n₀ информационных и k=n-n₀ проверочных (контрольных) символов, размещенных на определенных позициях (систематические коды).

Основные показатели кода n и n₀ пишутся в скобках [(7,4) n=7 n₀=4]. Рассмотрим двухпозиционный циклический код (m=2), у которого элементы кодовых комбинаций «0» «1».

Совокупность кодовых комбинаций циклического (n, n₀) кода может быть записана в виде матрицы, имеющей n символов в строке. В матрице n₀ строк линейно независимы.

Эти n₀ линейно- независимых строк n-разрядных кодовых комбинаций могут рассматриваться как образующая матрица, у которой строки связаны условием цикличности.

Все строки образующей матрицы циклического кода могут быть получены циклическим сдвигом одной кодовой комбинации, называемой образующей для данного кода. Сдвиг осуществляется справа налево, при этом крайний левый символ при образовании последующей комбинации переносится на крайнее правое место и т.д. Например, образующая матрица имеет вид

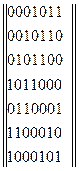(1.11.19)

В соответствии с теорией циклических кодов n-разрядная кодовая комбинация представляется в виде многочлена (полинома) с фиктивной переменной х. Наименьшему разряду, располагаемому в многочлене справа, соответствует фиктивная переменная х⁰=1. Номера разрядов многочлена, начиная с нулевого, соответствуют показателям степени х, а коэффициент K при х для рассматриваемых двухпозиционных кодов равен «0» или «1». n-разрядный полином с коэффициентом при х =1 будет иметь вид:

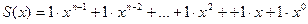(1.11.20)

Коэффициенты многочлена принято не писать, а с коэффициентом «0» опускать. Так для пятиразрядной (n=5) кодовой комбинации 01011 многочлен будет иметь вид:

S(x)= x³ + x +1.

В любом многочлене наибольшая степень x с коэффициентом 1 называется степенью многочлена. Так приведенный многочлен соответствует 3-й степени.

Сложение и вычитание многочленов равносильны и производятся по модулю 2

(обозначается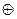). При этом суммируются только члены с одинаковой степенью x без переноса 1 в более старший разряд по следующим правилам:

0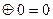

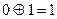
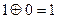
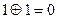
Если суммируется несколько чисел. То четное число единиц в сумме дает 0. Для примера сложим 3 многочлена и соответствующие им комбинации 8 - разрядного кода (n=8)

x⁷+ x⁵+ x³+ x²+1 → 10101101

x⁵+x¹+1 → 00100011

x⁷+ x⁶+ x⁵+ x¹+1 → 11100011.

При суммировании многочлены расположим таким образом, чтобы члены с одинаковыми степенями находились друг под другом, при этом справа будут суммироваться кодовые комбинации, соответствующие многочленам:

x⁷+0 + x⁵+ 0+x³+ x²+0 +1 → 10101101

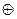
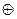
0 +0 + x⁵+ 0+ 0 + 0 +x¹+1 → 00100011

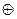
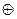
x⁷+x⁶+x⁵+ 0+ 0 + 0 + x¹+1 → 11100011

0+ x⁶+x⁵+ 0+ x³+ x²+0 +1 → 01101101

Умножение каждого многочлена на x повышает степень каждого многочлена на 1, на x² – на 2, т.е. умножение на xⁿ повышает степень на n. Это соответствует для кодовых комбинаций передвижению их в регистре на одну, две или n ячеек. Следовательно, умножение на x ⁱ соответствует приписывании. Справа i нулей или передвижению кодовых комбинаций в регистре на i ячеек и не требует какой-либо другой дополнительной аппаратуры.

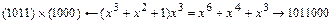
умножение соответствует добавлению 3-х нулей справа.

Умножение одного многочлена на другой состоит из двух этапов:

1. умножения одного многочлена на другой по правилам обычной алгебры, за исключением входящих в многочлен операций сложения;

2. операции сложения по модулю 2.

Например:

x⁴+ 0 + x²+ x + 1 → 10111

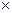
x³+ 0 + x + 1 → 1011

x⁴+ 0 + x²+ x + 1 → 10111

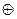
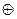
x⁵+0 + x³+ x²+ x + 0 → 10111

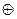
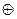
x⁷+ 0 +x⁵+x⁴+ x³+ 0 + 0 + 0 → 10111___

= x⁷+1 → 10000001

Для циклических кодов приведенные правила умножения выполняются, если суммарная степень полученного многочлена, которая определяется заданным n – разрядным кодом (а соответственно для регистра сдвига - числом n ячеек регистра, замкнутых в кольцо) не превышает n-1.

Деление одного многочлена на другой производится по правилам обычной алгебры, за исключением входящих в деление операций вычитания, которые здесь равносильны сложению и производятся по модулю 2. Деление производится до тех пор, пока степень остатка не станет меньше степени делителя, что соответствует числу разрядов остатка.

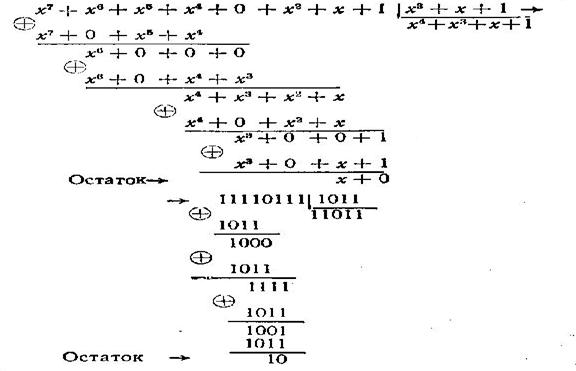Например:

Т.о. были рассмотрены операции умножения, сложения, и деления многочленов, на которых основаны принципы кодирования и декодирования циклических кодов.

Среди множества многочленов существуют неприводимые, которые не могут быть представлены в виде произведения многочленов низших степеней. Они аналогичны простым числам в теории чисел, т.е. они также делятся без остатка только на себя и на единицу.

В циклических кодах многочлен из разрешенной комбинации делится на образующий без остатка, в качестве которого выбирается неприводимый многочлен.

Все другие многочлены без остатка не делятся и относятся к запрещенным кодовым комбинациям. Это легко позволяет по остатку обнаружить и исправить ошибку.

Отсюда любая разрешенная кодовая комбинация есть произведение образующего многочлена на многочлен исходной разрешенной последовательности с приведением результата по модулю .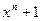

Как отмечалось, в качестве образующего многочлена выбирается неприводимый многочлен.

Так если выбрать n₀ – разрядный многочлен исходной последовательности (исходного сообщения) S_и (x), который соответствует n₀ – разрядной комбинации неизбыточного кода и умножить на неприводимый многочлен, выбранный как образующий (и просуммировать по модулю 2), то получим исходную комбинацию в циклическом коде и повторив комбинацию для всех n₀ – разрядных комбинаций исходного сообщения S_и (x) получим исходное сообщение в циклическом коде.

Но такой код очень не удобен, т.к. его контрольные K символы могут разместиться в любых позициях, что затрудняет декодирование. Что если разместить контрольные символы в конце строки после информационных? Действительно, пусть требуется получить циклический код в виде F(x) из исходной неизбыточной последовательности:

1. Задается многочлен сообщения S_и(x), соответствующий n₀ – разрядной информационной кодовой комбинации неизбыточного двухпозиционного (или бинарного) кода. Умножим его на образующий многочлен x^k.

Здесь k = n - n₀ - число контрольных символов, и оно равно степени образующего многочлена. Практически, такое умножение, как уже отмечалось, равносильно добавлению k нулей справа, или продвижению регистра сдвига с записанной в нем информационной кодовой комбинацией на k ячеек.

Выбор образующего многочлена состоит в том что:

2. к произведению x^kS_и(x) добавляют остаток R(x) от деления x^kS_и(x) на образующий многочлен P(x).

Это вытекает из следующего:

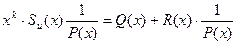, (1.11.21)

здесь Q (x)- частное от деления без учета остатка, R(x)- остаток от деления, равный вектору ошибки.

Умножим обе части уравнения (1.11.20) на P (x).

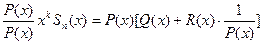
получим

x^k S_и (x)= Q(x)P(x) + R(x) (1.11.22)

здесь 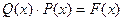- искомый многочлен циклического кода, из (1.11.22) имеем (после суммирования по модулю 2):

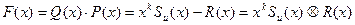, т.к. сложение и вычитание (по модулю 2) равносильны.

И получаем многочлен циклического кода.

Для обнаружения ошибки в принятой кодовой комбинации необходимо, чтобы операция деления на образующий многочлен

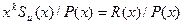(1.11.23)

давала остаток R (x) - вектор ошибки, определяющий местоположение ошибки.

При обнаружении однократных ошибок в кодовой комбинации полином ошибки R (x) записывается в виде 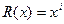, здесь i номер разряда, в котором произошла ошибка.

Так для i = 2 R (x)=100, т.е. ошибка во втором разряде. Для простейшего образующего полинома P (x)= x+1 условие обнаружения однократной ошибки удовлетворяется, т.к. частное .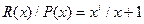

Для обнаружения однократных и двукратныхошибок условие обнаружения будет:

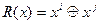, где i< n> j.

Полином P (x) принадлежит степени b, если b - наименьшее положительное число, при котором 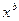+1 делится на P (x) без остатка и тогда для произвольного k существует не менее одного полинома P(x) степени k, удовлетворяющего условию:

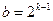(1.11.24)

Так для k = 3, 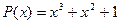и тогда 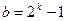=7

Т.е. 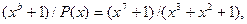остаток R’(x)=0

Следовательно, полином 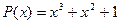принадлежит степени b = 7 и код порожденный полиномом P(x) обнаруживает однократные и двукратные ошибки, если длина кодовой комбинации n не больше показателей степени b.

Аналогично, для любой b -разрядной комбинации можно найти полином степени k, позволяющий обнаруживать одно- и двукратные ошибки b = 2^k -1. При этом .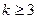

Для k = 2, n_и =1 и k = 3, b = n = 7 этому соответствует циклический код, образующий полином .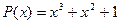

В общем случае, число k определяется из условия (1.11.25)

При этом k округляется до ближайшего целого числа (это обозначают фигурные скобки).

Для кодов с большими исправляющими возможностями (d > 3) применяют следующие формулы:

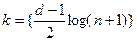для нечетного d

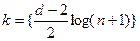для четного d

Для примера рассмотрим кодирование циклическим кодом исходного многочлена (полинома) сообщения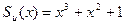

Пусть кодовое расстояние d=3 и n₀ =4 информативные символы, тогда для d=3 по (1.11.25) выбираем 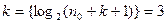, т.к. k=n-n₀, то n= n₀+k, т.е. n должно быть не менее 4+3.

Из таблицы для к = 3 выбираем неприводимый (образующий) многочлен (полином) Р(х) степени не ниже k, у которого число ненулевых членов Р(х) должно быть не меньше кодового расстояния d.

Таблица аналогична таблице простых чисел

k	Неприводимый полином	Двоичный эквивалент	Десятичный эквивалент
	x+1
	x^2+x+1
	x^3+x+1
	x^3+x^2+1
	X^4+1
	X^4+x+1
	X^4+x^3+1
	X^4+x^3+x^2+x+1
	x^5+x^2+1
	x^5+x^3+1
	x^5+x^3+x^2+x+1
	x^5+x^4+x^2+x+1
	x^5+x^4+x^3+x+1
	x^5+x^4+x^3+x^2+1
	x^6+x+1
	x^7+x^3+1
	x^8+x^4+x^3+x^2+1
	x^9+x^4+1

2) Выбираем:

Р(х)=x³+x+1 → 1011

3) Умножим исходный многочлен S_и(x) на x^k :

x^k ∙S_и(x) = (x³+x²+1)∙ x³=x⁶+x⁵+x³→1101000

4) Разделим произведение x^k ∙S_и(x) на выбранный образующий полином Р(х):

x⁶+x⁵+x³ | x³+x+1

+ x⁶+x⁴+x³ x³+x²+x+1

x⁵+x⁴

+ x⁵+x³+x²

x⁴+x³+x²

+ x⁴+x²+x

x³+x

+ x³+x+1

Остаток 1

Следовательно:

[ x^k ∙S_и(x)/P(x)] = (x⁶+x⁵+x³ )/(x³+x+1) = x³+x²+x+1+1/(x³+x+1).

Аналогично для двоичной записи:

1101000 | 1011

1011 1111

+ 1011

+ 1011

+ 1011

0001 остаток

то есть:

x^k ∙S_n(x)/P(x) = 1101000/1011 = 1111 + 001/1011

по формуле:

S_n(x)/P(x)=Q(x)+R(x)/P(x)=x³+x²+x+1+1/(x³+x+1)→1111+001/1011.

Здесь:

Q(x)= x³+x²+x+1 → 1111

Остаток R(x)/P(x)=1/(x³+x+1) → 001/1011

5) Искомый многочлен циклического кода F(x) из ф.1.11.21 и ф.1.11.22. будет:

F(x) = Q(x)P(x) = x^k ∙S_n(x)+R(x)=x⁶+x⁵+x³+1→1111∙1011=1101000+001=1101001.

То есть в начале полученной кодовой комбинации циклического кода размещается n₀ информационных символов S_n(x)→1101 и в конце k = 3 контрольных символов 001.

Операция умножения исходного полинома сообщения S_n(x) на x^k осуществляется в регистре сдвига путём сдвига записанной в нём исходной комбинации S_и(x)= x³+x²+1→1101 на k = 3 ячеек, а деление на образующий многочлен Р(х) выполняется на регистре сдвига с обратными связями, включёнными через сумматоры по модулю два. Число таких сумматоров равно числу отличных от нуля членов P(x) без учёта старшего разряда. Это объясняется тем, что сумма по модулю два старших разрядов многочлена S_и(x) и многочлена Р(х) всегда равна нулю.

Деление полиномов сводится к сложению по модулю два делителя вначале со старшими слагаемыми делимого, затем со старшими слагаемыми получающегося остатка, начиная с первого слагаемого, отличающегося от нуля.

Процесс деления продолжается до тех пор, пока степень остатка не будет меньше степени делителя (пока делится - делить). Отсюда для деления произвольного полинома на приводимый полином Р(х) со степенью k =n-n₀ необходим регистр с числом ячеек k.

Алгоритм кодирования при делении сообщения S_и(x) на неприводимый (образующий) полином Р(х) определяется выражением ф.1.11.22. Для этого, как отмечалось ранее, используется k - разрядный регистр сдвига с обратными связями через сумматоры по модулю 2. Структурная схема такого кодирующего устройства для неприводимого полинома степени k без нулевых слагаемых приведена на рис.

Рис. Кодирующее устройство для циклического кода с k-разрядным регистром сдвига.

Рис.1.12 Кодирующее устройство для неприводимого (образующего) полинома .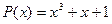

В начале кодирования ключ П₁ находится в положении 1, а ключ П₂ замкнут. Информационная кодовая комбинация (исходная) из n₀ импульсов подаётся непосредственно на выход и одновременно в регистр и за n₀=n-k тактов формируется остаток R(х), состоящий из контрольных символов. После этого ключ П₂ размыкается, а ключ П₁ переключается в положение 2 и контрольные символы за последующие k=n-n₀ тактов выводятся из регистра сразу за информационными символами.

Аналогично работает устройство для получения неприводимого (образующего) полинома (рис Б).

Самостоятельно:

Ф.Е. Темников, В. А. Фонин. «Теоретические основы информационной техники», глава 3.

В. А. Ильин «Телеуправление и телеизмерение», глава 3.

Дата добавления: 2014-01-06