Def. Отображение, сохраняющее отношение инцидентности называется гомоморфизмом графа

Def. Путем в нечетком графе называется такой его нечеткий подграф из последовательных дуг, что конец каждой предыдущей дуги совпадает с концом следующей при условии

Def. Длиной пути графа называется число его дуг

Очевидно, дополнением нечеткого псевдогафа называется граф такой, что

" ‹s _I, V_J› Î V^2Þ Ms ‹V_i, V_j› = 1- Ms ‹V_i, V_j› (см. случай для четких псевдографов дополнения)

" ‹V_i, V_J› Þ Ms ‹V_i, V_j› › 0

Гомоморфизм графа

Граф может быть гомоморфным графу, если:

f₁: V1® V’₂ f₂: ‹V₁, V₂› ® ‹V’₂, V’₂›

V_2® V’₂ ‹V₂, V₃› ® ‹V’₁, V’₂›

V_3® V’₁ ‹V₃, V₁› ® ‹V’₁, V’₂›

Частные случаи: автоморфизм и изоморфизм.

Классификация графов специального вида.

Замкнутый граф: все дуги (ребра) составляют простой путь, или простой контур(цикл)

Двудольный граф (s = ‹V₁,V₂,U›;V₁ Ç V₂= Æ V₁ È V₂=V²), в котором можно выделить такие два подмножества вершин, что эти подмножества не пересекаются между собой.

Бихроматический граф – это граф, вершины которого можно окрасить 2-мя цветами с тем, чтобы никакие смежные вершины не имели одинакового цвета.

Дерево(прадерево) – это связный неограф(орграф) с наименьшим числом ребер. Дерево - это ациклический граф, в котором число вершин на одно больше числа ребер. Любое дерево по средствам раскраски в два цвета можно представить двудольным графом. Лес - это несвязный граф, компоненты связности которого являются деревья.

Сепарабельным(односвязным) графом называют граф, имеющий хотя бы одну точку сочленения, это вершины которые превращают связный граф в несвязный, ребро обладающее таким же свойством называется мостом.

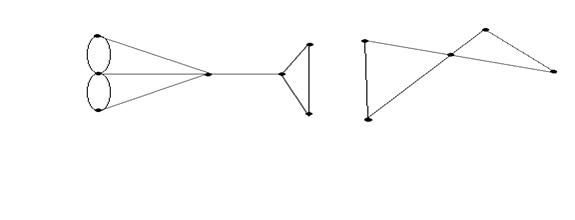
Несепарабельный граф – это граф без точек сочленения. Однордный регулярный неограф - это граф степень вершин которого одинакова.

Первая теорема Эйлера

Полный неограф – это однородный граф, все вершины которого попарно смежны, т.е. степень каждой вершины degV_i =|V| - 1

|U| = ½ |V|*|V – 1|

Двудольный граф называется полным, если множество его ребер есть произведение мощностей его долей.

U =V₁ ´ V₂

Турнир – это орграф, если две вершины его соединены одной и только одной дугой(если основание орграфа является полный неограф.

Плоский граф – это граф, дуги (ребра) которого не пересекаются нигде кроме инцидентных им вершин. Планарый граф - это граф изоморфный плоскому графу.

Достаточным признаком планарности графа является выражение

|U|£ (|V|+2)

Разбиение плоскости плоским графом на отдельные области называется плоской картой. Критерием планарного графа является теорема Эйлера.

|V| - |U| + |Г| = 2,

где |V| - мощность множества вершин, |U| - мощность множества ребер, |Г| - мощность множества граней. Формула Эйлера с помощью цикломатического числа:

| Г| = g +1; где g = |U| - |V| + 1

Триангулированный – максимальный планарный граф, т.е. граф, при добавлении ребра в который, перестает быть плоским. Плоская карта триангулированного графа есть множество граней, ограниченных тремя ребрами, в этом случае карту называют триангулированной. Число ребер плоской триангулированной равна

|U| = 3(|V| - 2); |Г| = 2(|V| - 2)

Минимальный неплоский граф – это неплоский граф, удаление ребра которого делает его плоским.

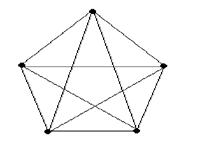
Теорема. Граф плоский тогда и только тогда, когда он не содержит подграфа гомоморфного графу К_3,3 и К₅

Граф гамильтонов – это граф, в котором имеется простой цикл, содержащий каждую вершину этого графа. Эйлеров граф – это граф, в котором цикл содержит все ребра.

Дата добавления: 2014-01-06