Лекция № 6

Разбиение множества на классы с помощью свойств

Разбиение множества на классы

Лекция № 5

В жизни приходится сталкиваться с задачами классификации. Предположим, что при сборе яблок в саду нужно определить какие яблоки необходимо сохранить до зимы, какие следует съесть сразу, а какие предназначены на переработку. С точки зрения математики, множества всех собранных яблок разбивается на три непересекающихся множества: А₁, А₂, А₃.

В науке проблема классификации является одной из самых важных задач. Особенно хорошо это видно на примере ботаники, где существует очень сложная «многоступенчатая» классификация растений.

В математике буквально с первых лет обучения дети узнают, что бывают числа, записываемые с помощью одного знака и двух знаков. Более старшие ученики узнают, что есть еще трехзначные, четырехзначные и т. д. записи чисел.

В этом примере множество всех натуральных чисел оказалось разбитым на бесконечное число классов по количеству цифр в десятичной записи чисел.

Классификацию выполняют достаточно часто. Например, натуральные числа представляем как два класса – четные и нечетные. Углы на плоскости разбиваем на три класса: прямые, острые и тупые.

Определение. Любая классификация связана с разбиением некоторого множества объектов на подмножества. При этом считают, что множество Х разбито на классы Х₁,Х₂… Х_n,…, если:

1. подмножества Х₁,Х₂… Х_n, … не пересекаются,

2. объединение подмножеств Х₁,Х₂… Х_n, … совпадает с множеством Х.

Если не выполнено хотя бы одно из условий, классификацию считают неправильной. Например, если из множества треугольников выделить подмножества равнобедренных, равносторонних, разносторонних треугольников, то разбиения мы не получим, так как подмножества равнобедренных и равносторонних треугольников пересекаются (не выполнено первое условие классификации).

Так как разбиение множества на классы связано с выделением его подмножеств, то классификацию можно выполнять при помощи свойств элементов множеств.

Рассмотрим, например, множество натуральных чисел. Его элементы обладают разными свойствами. Предположим, что нас интересуют числа, обладающие свойством “быть кратным 3”. Это свойство позволяет выделить из множества натуральных чисел подмножество, состоящее из чисел, кратных 3. Тогда про остальные числа можно сказать, что они не кратны 3, т.е. получаем еще одно подмножество множества натуральных чисел. Так как выделенные подмножества не пересекаются, а их объединение совпадает с множеством натуральных чисел, то получаем разбиение этого множества на два класса.

N

Вообще, если на множестве Х задано одно свойство, то это множество разбивается на два класса. Первый – класс, обладающий этим свойством, а второй – класс объектов, не обладающих этим свойством.

Такая классификация называется дихотомической.

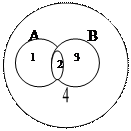
Рассмотрим ситуацию, когда для элементов множества N заданы два свойства: “быть кратным 3” и “быть кратным 5”. При помощи этих свойств из множества натуральных чисел можно выделить два подмножества: А – подмножество чисел кратных 3, В – подмножество чисел кратных 5. Эти множества пересекаются, но ни одно из них не является подмножеством другого.

N

Разбиения множества натуральных чисел на подмножества А и В не произошло, но круг, изображающий множество N, можно рассматривать как состоящий из четырех непересекающихся областей. Каждая область изображает некоторое подмножество множества N:

1– множество чисел кратных 3, но не кратных 5,

2– множество чисел кратных 3 и кратных 5,

3– множество чисел кратных 5, но не кратных 3,

4– множество чисел не кратных 3 и не кратных 5.

Объединение этих четырех подмножеств есть множество N.

Таким образом, выделение двух свойств привело к разбиению множества N натуральных чисел на четыре класса.

Не всегда задание двух свойств элементов множества приводит к разбиению этого множества на 4 класса. Например, при помощи двух свойств «быть кратным 3» и «быть кратным 6» множество натуральных чисел разбивается на три класса: I– класс чисел, кратных 6, II– класс чисел, кратных 3, но не кратных 6, III– класс чисел, не кратных 3.

Рассмотрим случай, когда есть 3 свойства: 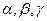. В общем случае разбиение множества на классы изображено следующим образом:

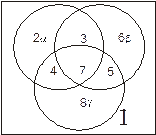
Нетрудно подсчитать, что получилось в этом случае восемь классов. Они помечены цифрами от 1 – 8. Класс, обозначенный цифрой 5, состоит из всех элементов множества, обладающих свойствами и 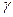и не обладающих свойством 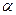. Класс 7 состоит из всех элементов, обладающих свойствами .

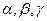Таким образом, можно подметить закономерность: при разбиении множества на классы с помощью n свойств получается 2 ⁿ классов разбиения. Если это верно, то в случае 4-х свойств, классов должно быть 16.

Задание! Приведите пример и опишите задание из начальной школы, в котором применяется классификация объектов (с помощью одного и двух свойств).

Дата добавления: 2014-01-06