
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вектор. Основные свойства
|
|
|
|
Схема испытаний Бернулли
Пусть производится п независимых испытаний, в каждом из которых событие А может произойти либо не произойти. Условимся считать, что вероятность события А в каждом испытании одна и та же, а именно равна р. Следовательно, вероятность ненаступления события А в каждом испытании также постоянна и равна q =1– р. Такого рода схема испытаний называется схемой Бернулли.
Тогда вероятность того, что событие А наступит ровно m раз, находится по формуле Бернулли:
Рп(m)=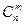 ×рm×qn–m,
×рm×qn–m,
где 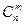 – число сочетаний из п элементов по m элементов.
– число сочетаний из п элементов по m элементов.
Пример. Игральную кость подбрасывают 10 раз. Найти вероятность того, что шестерка выпадет два раза.
Решение. Производится 10 независимых испытаний. Каждое испытание имеет два исхода: шестерка выпадет, шестерка не выпадет. Вероятность выпадения шестерки в каждом испытании постоянна и равна 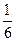 . Для нахождения искомой вероятности применим формулу Бернулли. Здесь п =10, m =2, р =
. Для нахождения искомой вероятности применим формулу Бернулли. Здесь п =10, m =2, р =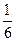 , q = 1 –
, q = 1 –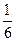 =
=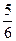 . Тогда Р10(2) =
. Тогда Р10(2) = 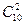 ×(
×(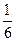 )2×(
)2×(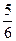 )10–2 = 45×
)10–2 = 45×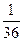 ×(
×(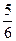 )8 » 0,291.
)8 » 0,291.
Определение. Вектор – Упорядоченную совокупность 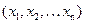 n вещественных чисел называют n -мерным вектором, а числа
n вещественных чисел называют n -мерным вектором, а числа 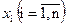 - компонентами, или координатами, вектора.
- компонентами, или координатами, вектора.
Пример 1.1. Если, например, некоторый автомобильный завод должен выпустить в смену 50 легковых автомобилей, 100 грузовых, 10 автобусов, 50 комплектов запчастей для легковых автомобилей и 150 комплектов для грузовых автомобилей и автобусов, то производственную программу этого завода можно записать в виде вектора (50, 100, 10, 50, 150), имеющего пять компонент.
Обозначения. Векторы обозначают жирными строчными буквами или буквами с чертой или стрелкой наверху, например, a или `a. Два вектора называются равными, если они имеют одинаковое число компонент и их соответствующие компоненты равны.
|
|
|
Компоненты вектора нельзя менять местами, например, (3, 2, 5, 0, 1) ¹
¹ (2, 3, 5, 0, 1).
Операции над векторами. Произведением вектора 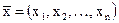 на действительное число l называется вектор
на действительное число l называется вектор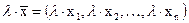
Суммой векторов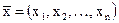 и
и 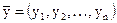 называется вектор
называется вектор 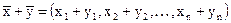 .
.
Пространство векторов. N - мерное векторное пространство R n определяется как множество всех n-мерных векторов, для которых определены операции умножения на действительные числа и сложение.
Экономическая иллюстрация. Экономическая иллюстрация n-мерного векторного пространства: пространство благ (товаров). Под товаром мы будем понимать некоторое благо или услугу, поступившие в продажу в определенное время в определенном месте. Предположим, что существует конечное число наличных товаров n; количества каждого из них, приобретенные потребителем, характеризуются набором товаров
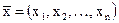 ,
,
где через xi обозначается количество i-го блага, приобретенного потребителем. Будем считать, что все товары обладают свойством произвольной делимости, так что может быть куплено любое неотрицательное количество каждого из них. Тогда все возможные наборы товаров являются векторами пространства товаров 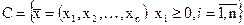 .
.
Линейная независимость. Система 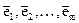 n-мерных векторов называется линейно зависимой, если найдутся такие числа
n-мерных векторов называется линейно зависимой, если найдутся такие числа 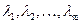 , из которых хотя бы одно отлично от нуля, что выполняется равенство
, из которых хотя бы одно отлично от нуля, что выполняется равенство 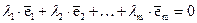 ; в противном случае данная система векторов называется линейно независимой, то есть указанное равенство возможно лишь в случае, когда все
; в противном случае данная система векторов называется линейно независимой, то есть указанное равенство возможно лишь в случае, когда все 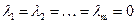 . Геометрический смысл линейной зависимости векторов в R 3, интерпретируемых как направленные отрезки, поясняют следующие теоремы.
. Геометрический смысл линейной зависимости векторов в R 3, интерпретируемых как направленные отрезки, поясняют следующие теоремы.
Теорема 1. Система, состоящая из одного вектора, линейно зависима тогда и только тогда, когда этот вектор нулевой.
Теорема 2. Для того, чтобы два вектора были линейно зависимы, необходимо и достаточно, чтобы они были коллинеарны.
|
|
|
Теорема 3. Для того, чтобы три вектора были линейно зависимы, необходимо и достаточно, чтобы они были компланарны.
Левая и правая тройки векторов. Тройка некомпланарных векторов 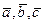 называется правой, если наблюдателю из их общего начала обход концов векторов
называется правой, если наблюдателю из их общего начала обход концов векторов 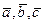 в указанном порядке кажется совершающимся по часовой стрелке. B противном случае
в указанном порядке кажется совершающимся по часовой стрелке. B противном случае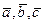 - левая тройка. Все правые (или левые) тройки векторов называются одинаково ориентированными.
- левая тройка. Все правые (или левые) тройки векторов называются одинаково ориентированными.
Базис и координаты. Тройка 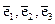 некомпланарных векторов в R 3 называется базисом, а сами векторы
некомпланарных векторов в R 3 называется базисом, а сами векторы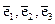 - базисными. Любой вектор
- базисными. Любой вектор 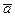 может быть единственным образом разложен по базисным векторам, то есть представлен в виде
может быть единственным образом разложен по базисным векторам, то есть представлен в виде
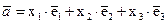 (1.1)
(1.1)
числа 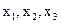 в разложении (1.1) называются координатами вектора
в разложении (1.1) называются координатами вектора 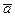 в базисе
в базисе 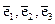 и обозначаются
и обозначаются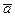
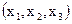 .
.
Ортонормированный базис. Если векторы 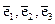 попарно перпендикулярны и длина каждого из них равна единице, то базис называется ортонормированным, а координаты
попарно перпендикулярны и длина каждого из них равна единице, то базис называется ортонормированным, а координаты 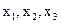 - прямоугольными. Базисные векторы ортонормированного базиса будем обозначать
- прямоугольными. Базисные векторы ортонормированного базиса будем обозначать 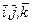 .
.
Будем предполагать, что в пространстве R 3 выбрана правая система декартовых прямоугольных координат 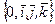 .
.
Векторное произведение. Векторным произведением вектора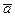 на вектор
на вектор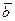 называется вектор
называется вектор 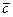 , который определяется следующими тремя условиями:
, который определяется следующими тремя условиями:
1. Длина вектора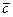 численно равна площади параллелограмма, построенного на векторах
численно равна площади параллелограмма, построенного на векторах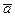 и
и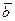 , т. е.
, т. е. 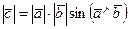 .
.
2. Вектор 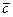 перпендикулярен к каждому из векторов
перпендикулярен к каждому из векторов 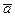 и
и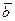 .
.
3. Векторы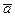 ,
, 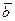 и
и 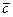 , взятые в указанном порядке, образуют правую тройку.
, взятые в указанном порядке, образуют правую тройку.
Для векторного произведения 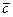 вводится обозначение
вводится обозначение 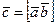 или
или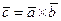 .
.
Если векторы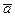 и
и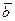 коллинеарны, то
коллинеарны, то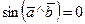 и
и 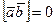 , в частности,
, в частности, 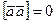 . Векторные произведения ортов:
. Векторные произведения ортов: 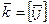 ,
,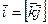 ,
,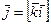 .
.
Если векторы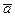 и
и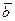 заданы в базисе
заданы в базисе 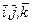 координатами
координатами 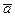
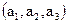 ,
, 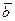
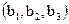 , то
, то 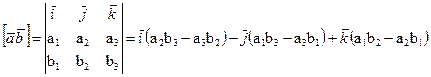
Смешанное произведение. Если векторное произведение двух векторов 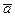 и
и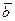 скалярноумножается на третий вектор
скалярноумножается на третий вектор 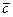 , то такое произведение трех векторов называется смешанным произведением и обозначается символом
, то такое произведение трех векторов называется смешанным произведением и обозначается символом 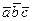 .
.
Если векторы 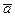 ,
, 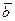 и
и 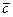 в базисе
в базисе 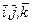 заданы своими координатами
заданы своими координатами
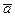
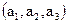 ,
, 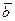
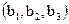 ,
, 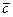
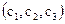 , то
, то
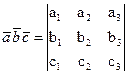 .
.
Смешанное произведение имеет простое геометрическое толкование - это скаляр, по абсолютной величине равный объему параллелепипеда, построенного на трех данных векторах.
Если векторы образуют правую тройку, то их смешанное произведение есть число положительное, равное указанному объему; если же тройка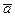 ,
, 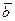 ,
, 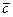 - левая, то
- левая, то 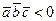 и
и 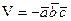 , следовательно
, следовательно 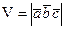 .
.
|
|
|
Координаты векторов, встречающиеся в задачах первой главы, предполагаются заданными относительно правого ортонормированного базиса. Единичный вектор, сонаправленный вектору 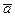 , обозначается символом
, обозначается символом 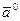 . Символом
. Символом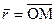 обозначается радиус-вектор точки М, символами
обозначается радиус-вектор точки М, символами 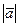 ,
, 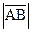 обозначаются модули векторов
обозначаются модули векторов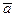 и
и 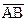 .
.
Пример 1.2. Найдите угол между векторами 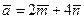 и
и 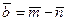 , где
, где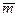 и
и 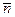 - единичные векторы и угол между
- единичные векторы и угол между 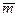 и
и 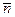 равен 120о.
равен 120о.
Решение. Имеем: 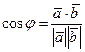 ,
, 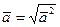 ,
,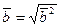
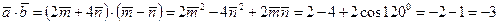
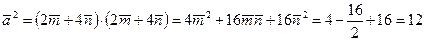 , значит
, значит 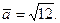
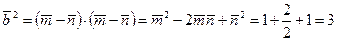 , значит
, значит 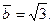
Окончательно имеем: 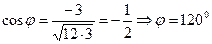 .
.
Пример 1.3. Зная векторы 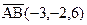 и
и 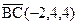 , вычислите длину высоты AD треугольника ABC.
, вычислите длину высоты AD треугольника ABC.
Решение. Обозначая площадь треугольника ABC через S, получим:
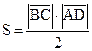 . Тогда
. Тогда 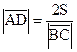 ,
,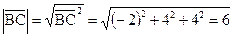 ,
,
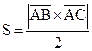 .
. 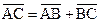 , значит, вектор
, значит, вектор имеет координаты
имеет координаты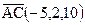 .
.
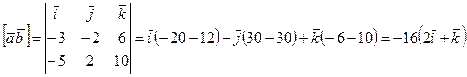 .
.
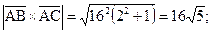
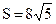 , откуда
, откуда 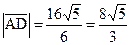 .
.
Пример 1.4. Даны два вектора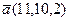 и
и 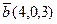 . Найдите единичный вектор
. Найдите единичный вектор 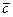 , ортогональный векторам
, ортогональный векторам 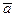 и
и 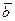 и направленный так, чтобы упорядоченная тройка векторов
и направленный так, чтобы упорядоченная тройка векторов 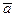 ,
, 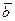 ,
, 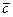 была правой.
была правой.
Решение. Обозначим координаты вектора 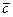 относительно данного правого ортонормированного базиса через
относительно данного правого ортонормированного базиса через 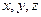 .
.
Поскольку 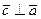 ,
, 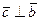 , то
, то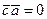 ,
, 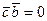 . По условию задачи требуется, чтобы
. По условию задачи требуется, чтобы 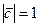 и
и 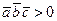 .
.
Имеем систему уравнений для нахождения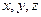 :
:
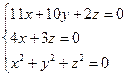
Из первого и второго уравнений системы получим 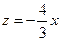 ,
,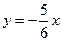 . Подставляя
. Подставляя 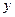 и
и 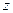 в третье уравнение, будем иметь:
в третье уравнение, будем иметь: 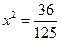 , откуда
, откуда 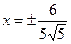 . Используя условие
. Используя условие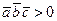 , получим неравенство
, получим неравенство
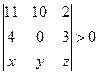 или
или 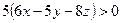
С учетом выражений для 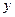 и
и 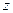 перепишем полученное неравенство в виде:
перепишем полученное неравенство в виде: 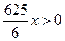 , откуда следует, что
, откуда следует, что 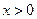 . Итак,
. Итак, 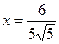 ,
, 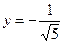 ,
, 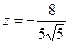 .
.
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 678; Нарушение авторских прав?; Мы поможем в написании вашей работы!